Study the given passage carefully & answer the questions in a sport Academy XY', there are some student who can play three games i.e tennis, cricket & chess. Total number of players who play tennis is 160 & all three games are played by 10% of total tennis players. Ratio of cricket to chess players is 3:5 and total of cricket & chess players is 100% more than tennis players. Players who play both tennis and chess are 1212% of total tennis players. Ratio of players who play both tennis & cricket to players who play both chess & cricket is 2:3 & total of players who play both tennis & cricket and players who play both chess & cricket is equal to one-fourth of chess players.
What is the average no. of players who play only one game?
13923
12913
135
None of these
The correct Answer is:B
To solve the problem step by step, we will break down the information provided and calculate the average number of players who play only one game.
Step 1: Determine the number of players for each game
- Total players who play tennis = 160
- Players who play all three games (Tennis, Cricket, Chess) = 10% of Tennis players = 10% of 160 = 16 players.
Step 2: Calculate the total number of players for Cricket and Chess
- The ratio of Cricket to Chess players is given as 3:5.
- Let the number of Cricket players be 3x and Chess players be 5x.
- The total number of Cricket and Chess players is 100% more than Tennis players:
- Total Cricket + Chess = 160 + 160 = 320.
So, we have:
3x+5x=320
8x=320
x=40
Now, we can find the number of players:
- Number of Cricket players = 3x = 3(40) = 120
- Number of Chess players = 5x = 5(40) = 200
Step 3: Determine the players who play both Tennis and Chess
- Players who play both Tennis and Chess = 12.5% of total Tennis players = 12.5% of 160 = 20 players.
Step 4: Determine the players who play both Tennis and Cricket and both Chess and Cricket
- Let the number of players who play both Tennis and Cricket be 2y and those who play both Chess and Cricket be 3y (from the ratio 2:3).
- The total of players who play both Tennis & Cricket and Chess & Cricket is equal to one-fourth of Chess players:
- Total = 1/4 of Chess players = 1/4 of 200 = 50.
So, we have:
2y+3y=50
5y=50
y=10
Now we can find the number of players:
- Players who play both Tennis and Cricket = 2y = 2(10) = 20
- Players who play both Chess and Cricket = 3y = 3(10) = 30
Step 5: Calculate the number of players who play only one game
- Players who play only Tennis = Total Tennis - (Players who play both Tennis & Cricket + Players who play both Tennis & Chess + Players who play all three)
- = 160 - (20 + 20 + 16) = 160 - 56 = 104
- Players who play only Cricket = Total Cricket - (Players who play both Tennis & Cricket + Players who play both Chess & Cricket + Players who play all three)
- = 120 - (20 + 30 + 16) = 120 - 66 = 54
- Players who play only Chess = Total Chess - (Players who play both Chess & Cricket + Players who play both Tennis & Chess + Players who play all three)
- = 200 - (30 + 20 + 16) = 200 - 66 = 134
Step 6: Calculate the average number of players who play only one game
- Total players who play only one game = Players who play only Tennis + Players who play only Cricket + Players who play only Chess
- = 104 + 54 + 134 = 292
- Average number of players who play only one game = Total players who play only one game / 3
- = 292 / 3 = 97.33
Final Answer
The average number of players who play only one game is approximately 97.33.
---
- Total players who play tennis = 160
- Players who play all three games (Tennis, Cricket, Chess) = 10% of Tennis players = 10% of 160 = 16 players.
- The ratio of Cricket to Chess players is given as 3:5.
- Let the number of Cricket players be 3x and Chess players be 5x.
- The total number of Cricket and Chess players is 100% more than Tennis players:
- Total Cricket + Chess = 160 + 160 = 320.
So, we have:
3x+5x=320
8x=320
x=40
- Number of Cricket players = 3x = 3(40) = 120
- Number of Chess players = 5x = 5(40) = 200
- Players who play both Tennis and Chess = 12.5% of total Tennis players = 12.5% of 160 = 20 players.
- Let the number of players who play both Tennis and Cricket be 2y and those who play both Chess and Cricket be 3y (from the ratio 2:3).
- The total of players who play both Tennis & Cricket and Chess & Cricket is equal to one-fourth of Chess players:
- Total = 1/4 of Chess players = 1/4 of 200 = 50.
So, we have:
2y+3y=50
5y=50
y=10
- Players who play both Tennis and Cricket = 2y = 2(10) = 20
- Players who play both Chess and Cricket = 3y = 3(10) = 30
- Players who play only Tennis = Total Tennis - (Players who play both Tennis & Cricket + Players who play both Tennis & Chess + Players who play all three)
- = 160 - (20 + 20 + 16) = 160 - 56 = 104
- = 120 - (20 + 30 + 16) = 120 - 66 = 54
- = 200 - (30 + 20 + 16) = 200 - 66 = 134
- Total players who play only one game = Players who play only Tennis + Players who play only Cricket + Players who play only Chess
- = 104 + 54 + 134 = 292
- = 292 / 3 = 97.33
The average number of players who play only one game is approximately 97.33.
Topper's Solved these Questions
- BOOK - ADDA247CHAPTER - DATA INTERPRETATIONEXERCISE - Mains Questions33videos
DATA INTERPRETATION
- BOOK - ADDA247CHAPTER - DATA INTERPRETATIONEXERCISE - Previous Year Questions56videos
DATA INTERPRETATION
- BOOK - ADDA247CHAPTER - DATA INTERPRETATIONEXERCISE - Prelims Questions (Level-1)54videos
DATA INTERPRETATION
- BOOK - ADDA247CHAPTER - BOAT AND STREAM EXERCISE - Previous Year Question22videos
BOAT AND STREAM
- BOOK - ADDA247CHAPTER - DATA SUFFICIENCY EXERCISE - PREVIOUS YEAR QUESTIONS25videos
DATA SUFFICIENCY
Similar Questions
Study the following diagram and answer questions based on it.
The number of Non-Chess players is how much more than the players who play both Chess and Tennis?
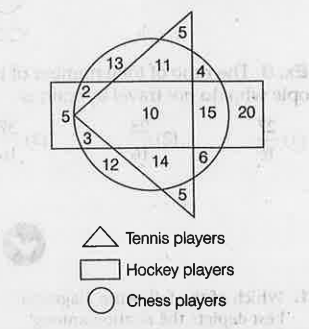 View Solution
View Solution30 Cricketers and 20 Kho-kho players are training on a field. What is the ratio of cricketers to the total number of players ?
View Solution
Knowledge Check
- Question 1 - Select One
Comprehension:
Study the following diagram and answer questions based on it.
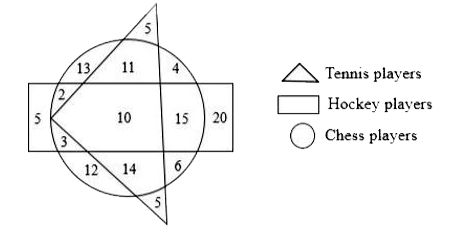
The number of non-chess players is how much more than the players who play both chess and tennis.A5B10CIt is the sameDCannot be determined - Question 2 - Select One
In a group of 60 persons, 40 persons like play cricket and 10 persons like play both Tennis and Cricket. Then, the number of persons who like to play Tennis, is
A20B25C30D40 - Question 3 - Select One
In a group of 60 persons, 40 persons like play cricket and 10 persons like play both Tennis and Cricket. Then, the number of persons who like to play Tennis, is
A20B25C30D40
In a group of 100 people, 60 people like to play cricket, 20 people like to play both cricket and Tennis. How many people like to play Tennis but not cricket?
View SolutionThe pie chart given below shows the number of students who play five sports like Hockey, Tennis Cricket, Golf and Polo. The total number of students is 1080.
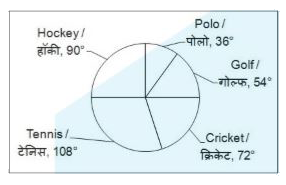
What is the average number of students playing Tennis and Cricket?View SolutionSome of the Cricket players are Tennis players, some Tennis players are Hockey players, no Cricket player is a Hockey player. Which one of the following diagrams represents the above statements?
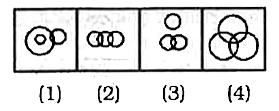 View Solution
View Solution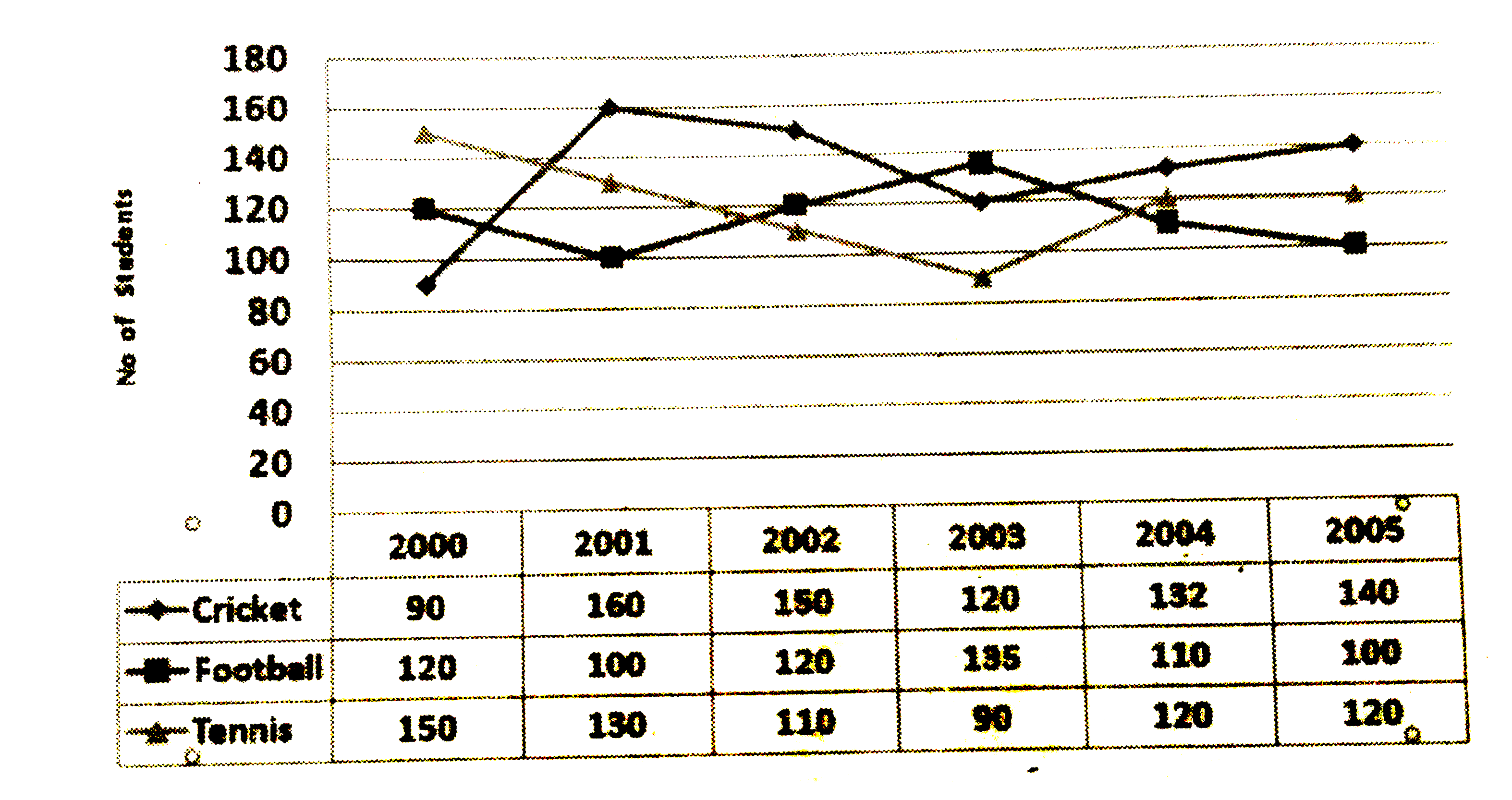
The total no of players who participated in all the 3 sports together in the year 2004 was What % of the total no of players who participates in Tennis over all years together (approx) ?View SolutionSix players are to play doubles Tennis match. IF every possible player must play with every other possible player, then the number of matches to be played is
View Solution

