Two mass m1andm2 are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

Fix an inertial frame to the ground to observe the motion of the masses.
Let the tension in the rope be T(in fact, tension is the property of a point of the rope). In this case with ideal pulley (massless and frictionless) and ideal rope(inextensible,massless, and flexible), the tension will remain constant throughout the rope. Let the acceleration of m2 be vertically downwards, and accelerations on m1 also be a, vertically upwards. This is because the rope is inextensible, during motion, the length of the rope must not change, and the rope must not slacken either.
From the above statement, you must not conclude that the accelerations of the masses connected by a rope are always equal. The relationshop between the accelerations of the masses depends on the configuration of the pulley-rope system , which can be obtained from the fact that the length of an ideal rope must not change and the rope must not slacken.
Using eq. Σ→F=m→a for the force diagram of m1andm2
T−m1g=m1a ...(i)
m2g−T=m2a ...(ii)
Adding (i) and (ii) , m2g−m1g=m1a+m2a
a=(m2−m1m2+m1)g
substituting this value of a in (i) we get
T=m1g+m1(m2−m1m2+m1)g−2m1m2(m1+m2)g...(iv).

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Two masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
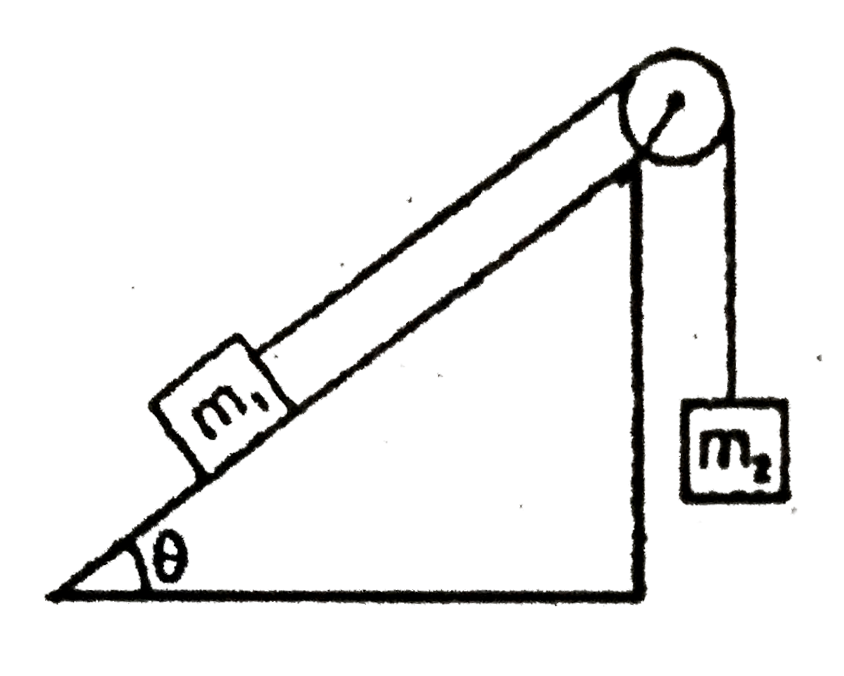
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses M1=5kg, M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
(a) g (b) g2 (c) g3 (d) g4
 View Solution
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo bodies of mass 4 kg and 6 kg tied to the ends of a massless string. the string passes over a pully which is frictionless (see figure). the acceleration of the system in terms of acceleration due to gravity (g) is:
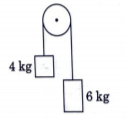 View Solution
View Solution

