A coin is at the bottom of a trough containing three immiscible liquids of refractive indices 1.3, 1.4 and 1.5 poured one above the other of heights 30 cm, 16 cm, and 20 cm respectively. What is the apparent depth at which the coin appears to be when seen from air medium outside? In which medium the coin will be seen?
When seen from top, the coin will still appear to be at the bottom with each medium appearing to have shrunk with respect to the air medium outside. This situation is illustrated below
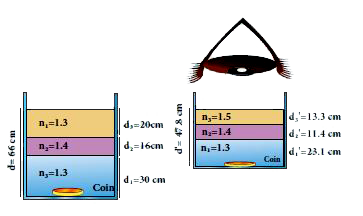
The equations for apparent depth for each medium is,
d.1=d1n1,d.2=d2n2, d.3=d3n3
d.=d.1+d.2+d.3=d1n1+d2n2+d3n3
Topper's Solved these Questions
- OPTICSBOOK - NCERT TAMILCHAPTER - OPTICSEXERCISE - EVALUATION (Multiple choice questions)
20 Videos
- OPTICSBOOK - NCERT TAMILCHAPTER - OPTICSEXERCISE - EVALUATION (Numerical Problems)
10 Videos
- NUCLEIBOOK - NCERT TAMILCHAPTER - NUCLEIEXERCISE - ADDITIONAL EXERCISES
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT TAMILCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISES
40 Videos
Similar Questions
Three immiscibles transparent liquids with erefractive indices 3/2,4/3 and 6/5 are arranged one on top of another. The depth of the liquid are 3 cm, 4 cm and 6 cm respectively. The apparent depth of the vessel is
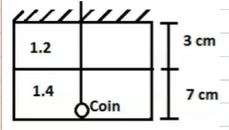
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
View Solution
Knowledge Check
Three immiscible transparent liquids with refractive indices 3/2,4/3 and 6/5 are arranged one on top of another. The depth of the liquid are 3cm,4cm and 6cm respectively. The apparent depth of the vessel is
A10cmB9cmC8cmD7cmTwo immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air
A3√2h4B3h4C3h2D3h4√2
A man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.

View SolutionTwo immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air
View SolutionA jar contains two immiscible liquids A and B with a coin at its bottom. The depths of liquid A and liquid B are 6 cm and 8 cm, respectively. If the apparent depth of the coin is 9 cm and refractive index of liquid A is 1.5, what is the refractive index of liquid B?
View SolutionAn object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View SolutionA coin at the bottom of a trough containing water to a depth of 15 cm appears to be 3.75 cm raised above from the bottom. Calculate the refractive index of water.
View Solution
