In Figure 1 , a triangle ABC with ∠B=90∘ is shown. Taking AB as diameter , a circle has been drawn intersection AC at point P . Prove that the tangent drawn at point P bisects BC.
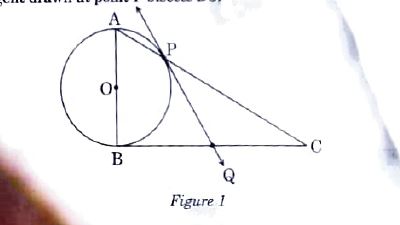
Step by step video & image solution for In Figure 1 , a triangle ABC with angleB = 90^@ is shown. Taking AB as diameter , a circle has been drawn intersection AC at point P . Prove that the tangent drawn at point P bisects BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View Solution
Knowledge Check
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
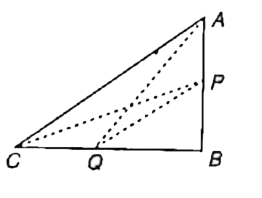 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)The tangents drawn at the end points of the diameter of a circle will be
Aperpendicular to each otherBparallel to each otherCinclined to each other at 45∘Dinclined to each other at 60∘
An isosceles triangle ABC, with AB = AC, circumscribes a circle, touching BC at P, AC at Q and AB at R. Prove that the contact point P bisects BC.
View SolutionIn ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionIn a △ABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ.
View SolutionABC is an isosceles triangle in which AB = AC. Prove that the tangent to the circum-circle at A is parallel to BC.
View SolutionΔABC is a right triangle which is right angled at C. A circle is drawn taking AB as a diameter. AC is extended to point P. BP meet semicircle at D, then AB2 =
View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
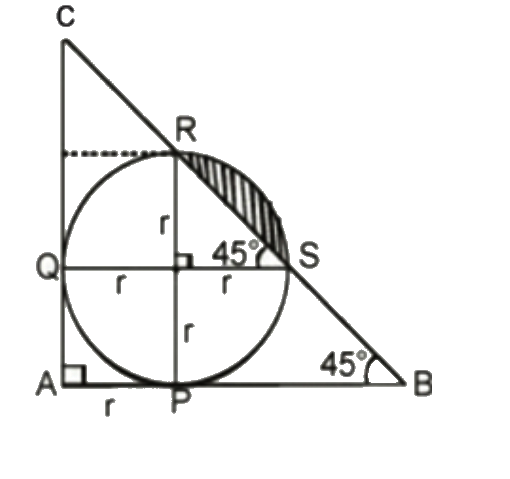
View Solution
