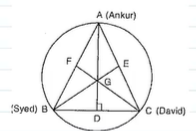
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
The correct Answer is:20√3m
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - NCERT SECTION (EXERCISE 10.5)2videos
CIRCLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - NCERT SECTION (EXERCISE 10.6)2videos
CIRCLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - NCERT SECTION (EXERCISE 10.1)9videos
CIRCLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Olympiad/HOTS Corner14videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONSTRUCTIONS EXERCISE - OLYMPIAD/HOTS CORNER5videos
CONSTRUCTIONS
Similar Questions
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed andDavid are sitting at equal distance on its boundary each having a toy telephone inhis hands to talk each other. Find the length of the string of each phone.
View SolutionA circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other.
 View Solution
View SolutionA horizontal weightless rod of length 3l is suspended on two vertical strings. Two loads of mass m1 and m2 are in equilibrium at equal distance from each other and from the ends of the strings (Fig). Determie the tension T of the left string at the instant when the right string snaps.
 View Solution
View SolutionFigure-2.107 shows a block of mass m attached to a spring of force constant k and connected to ground by two string of equal lengths making an angle 90∘ with each other. In relaxed state natural length of the spring is l. In the situation shown in figure, find the tensions in the two strings.
 View Solution
View SolutionThree thin unifrom circular discs each of mass M and radius R are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three discs are joined. Find the M.I. about an axis passing through the center of mass system of discs and perpendicular to the plane.
View SolutionA magnetic pole of strength qm is placed at a distance of 20 cm from another magnetic pole of triple its strength. If the two poles exert a force of 2.5 g f on each other, find the strength of each pole.
View SolutionDirection: In the following question, a given questions is followed by information in three statements. You have to decide the data in which statement (s) is sufficient to answer the question and mark your answer accordingly.
8 people – A, B, C, D, E, F, G and H are sitting around a circular table at equal distances to each other facing towards centre (not necessarily in the same order), then how many persons are sitting between C and D, if counted from the left of D.
C is sitting second to the left of F. Four persons are sitting between F and D.
A is sitting fourth to the right of D. Two persons are sitting between A and E.
B is sitting third to the right of G.View SolutionThree identical particles, each of mass m, are located in space at the vertices of an equilateral triangle of side length a. They are revolving in a circular orbital under mutual ravitational attraction. Find the speed of each particle. Find the acceleration of the centre of mass of a system comprising of any two particles. Assume that one of the particles suddenly loses its ability to exert gravitational force. Find the velocity of the centre of mass of the system of other two particles after this.
View Solution

