A body is projected 10m/s from an inclined plane of inclination 300. The angle of projection at 300. Find range
103
203
10
403
To solve the problem of finding the range of a body projected from an inclined plane at an angle of 30∘ with an initial speed of 10m/s, we can follow these steps:
1. Understanding the Problem:
- The body is projected from an inclined plane with an inclination of 30∘.
- The initial speed u=10m/s.
- The angle of projection with respect to the inclined plane is also 30∘.
2. Resolve Initial Velocity:
- The initial velocity can be resolved into two components:
- Along the inclined plane (x-direction): ux=ucos(30∘)
- Perpendicular to the inclined plane (y-direction): uy=usin(30∘)
Using the values:
ux=10cos(30∘)=10⋅√32=5√3m/s
uy=10sin(30∘)=10⋅12=5m/s
3. Calculate Time of Flight:
- The time of flight T can be calculated using the formula:
T=2uygcos(α)
where g=10m/s2 (acceleration due to gravity) and α=30∘.
T=2⋅510⋅cos(30∘)=1010⋅√32=105√3=2√3s
4. Calculate Range:
- The range R along the inclined plane can be calculated using:
R=ux⋅T−12gsin(α)T2
Substituting the values:
R=(5√3)⋅(2√3)−12⋅10⋅sin(30∘)⋅(2√3)2
R=10−12⋅10⋅12⋅43
R=10−206=10−103=10−3.33=303−103=203m
5. Final Answer:
- The range of the body along the inclined plane is:
R=203m≈6.67m
- The body is projected from an inclined plane with an inclination of 30∘.
- The initial speed u=10m/s.
- The angle of projection with respect to the inclined plane is also 30∘.
- The initial velocity can be resolved into two components:
- Along the inclined plane (x-direction): ux=ucos(30∘)
- Perpendicular to the inclined plane (y-direction): uy=usin(30∘)
ux=10cos(30∘)=10⋅√32=5√3m/s
uy=10sin(30∘)=10⋅12=5m/s
- The time of flight T can be calculated using the formula:
T=2uygcos(α)
where g=10m/s2 (acceleration due to gravity) and α=30∘.
T=2⋅510⋅cos(30∘)=1010⋅√32=105√3=2√3s
- The range R along the inclined plane can be calculated using:
R=ux⋅T−12gsin(α)T2
Substituting the values:
R=(5√3)⋅(2√3)−12⋅10⋅sin(30∘)⋅(2√3)2
R=10−12⋅10⋅12⋅43
R=10−206=10−103=10−3.33=303−103=203m
- The range of the body along the inclined plane is:
R=203m≈6.67m
Topper's Solved these Questions
Similar Questions
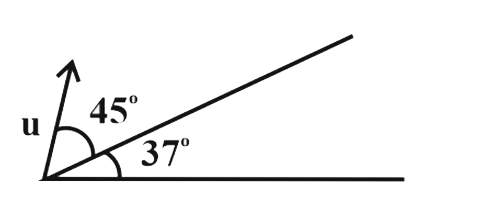
A particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View Solution
Knowledge Check
A body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
Ag2√2Bg2C3g2√2Dg√2A ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
A12 mB60 mC120 mD600 mA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
 A23B13C325D1√2
A23B13C325D1√2
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA ball is projected from the foot of an inclined plane of inclination 30∘ at an angle 60∘ with the horizontal,with velocity 20√3ms−1 .The time after which the ball will strike the plane is
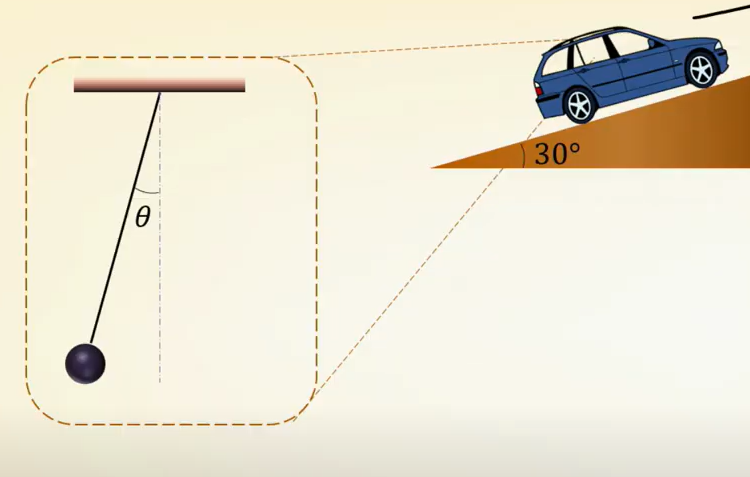
View SolutionA car is going with an acceleration of 10ms2 upwards on an inclined plane of inclination 300. There is a bob suspended in it. The angle θ which it makes with the vertical w.r.t ground is....
View SolutionA 2-kg body is sliding up an inclined plane of inclination 30∘. Find the work done by the force of gravity m moving the body through I m.
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View Solution
