A spring with spring constant K and length L was attached to a mass m and rotated about its axis at other end (in horizontal plane) with angular velocity w. Find elongation in spring
K−mw2Lmw2
K+mw2Lmw2
mw2LK−mw2
mw2LK+mw2
To solve the problem of finding the elongation in the spring when a mass m is attached to it and rotated with angular velocity ω, we can follow these steps:
1. Understand the System:
- We have a spring with spring constant K and natural length L.
- A mass m is attached to the end of the spring and is rotated in a horizontal circle.
2. Identify Forces:
- When the mass is rotated, it experiences a centripetal force that is required to keep it moving in a circular path.
- The spring will stretch due to this rotation, leading to an elongation X.
3. Determine the Radius of Rotation:
- The radius of the circular motion when the spring is elongated is R=L+X, where X is the elongation of the spring.
4. Centripetal Force Requirement:
- The centripetal force needed to keep the mass moving in a circle is given by:
Fc=mRω2=m(L+X)ω2
5. Spring Force:
- The force exerted by the spring when it is elongated by X is given by Hooke's law:
Fs=KX
6. Set Up the Equation:
- For the mass to maintain circular motion, the spring force must equal the centripetal force:
KX=m(L+X)ω2
7. Rearrange the Equation:
- Expanding the right side gives:
KX=mLω2+mXω2
- Rearranging this leads to:
KX−mXω2=mLω2
- Factoring out X from the left side:
X(K−mω2)=mLω2
8. Solve for Elongation X:
- Finally, we can solve for X:
X=mLω2K−mω2
Final Answer:
The elongation in the spring is given by:
X=mLω2K−mω2
- We have a spring with spring constant K and natural length L.
- A mass m is attached to the end of the spring and is rotated in a horizontal circle.
- When the mass is rotated, it experiences a centripetal force that is required to keep it moving in a circular path.
- The spring will stretch due to this rotation, leading to an elongation X.
- The radius of the circular motion when the spring is elongated is R=L+X, where X is the elongation of the spring.
- The centripetal force needed to keep the mass moving in a circle is given by:
Fc=mRω2=m(L+X)ω2
- The force exerted by the spring when it is elongated by X is given by Hooke's law:
Fs=KX
- For the mass to maintain circular motion, the spring force must equal the centripetal force:
KX=m(L+X)ω2
- Expanding the right side gives:
KX=mLω2+mXω2
- Rearranging this leads to:
KX−mXω2=mLω2
- Factoring out X from the left side:
X(K−mω2)=mLω2
- Finally, we can solve for X:
X=mLω2K−mω2
The elongation in the spring is given by:
X=mLω2K−mω2
Topper's Solved these Questions
Similar Questions
A uniform rod of mass M and length L with two particles m and m2 attached to its ends, is pivoted at its centre. The system rotates in a vertical plane with angular velocity ω.

View SolutionAn underformed spring with the spring constant k has length l0. When the system (Fig.) rotates at an angular
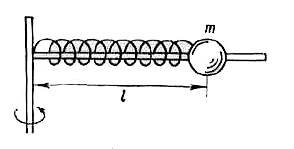
velocity ω, the weight with mass m causes an extension of the spring. Find the length l of the rotating spring.
View Solution
Knowledge Check
A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
Amω2l0kBmω2l0k−mω2Ckl0k−mω2Dmω2l0k+mω2A particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of theseA mass m attached to spring of natural length l0 and spring constant k. One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k>>mω2 ) :
Amω2kB√23mω2kCmω22kD3mω2k

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionOne end of a light spring constant k and natural length l0 is fixed and the other end is attached to a block of mass m lying on smooth horizontal surface. If the block is rotating in the horizontal circle of radius l, find the frequency of the revolution.
View SolutionA particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l. The other end of the spring is fixed on a vertical axis which is rotaing with an angular velocity ω. The increase in length of th espring will be

View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionAn ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
View Solution
