A thin lens of focal length f in meter is cut into two parts symmetrically as shown. Then the power of part A is 
1/f
1/2f
2/f
1/3f
Step by step video & image solution for A thin lens of focal length f in meter is cut into two parts symmetrically as shown. Then the power of part A is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A double convex lens of focal length is cut into 4 equal parts One cut is perpendicular to the axis and the other is parallel to the axis of lens. The focal length of each part is
View SolutionAn equiconvex lens of focal length 15cm is cut into two equal halves in thickness. What is the focal length of each half ?
View Solution
Knowledge Check
If a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:
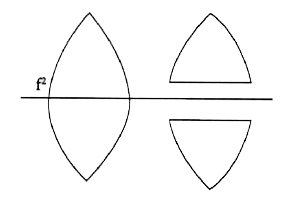 Af2Bf4CfD∞
Af2Bf4CfD∞A convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
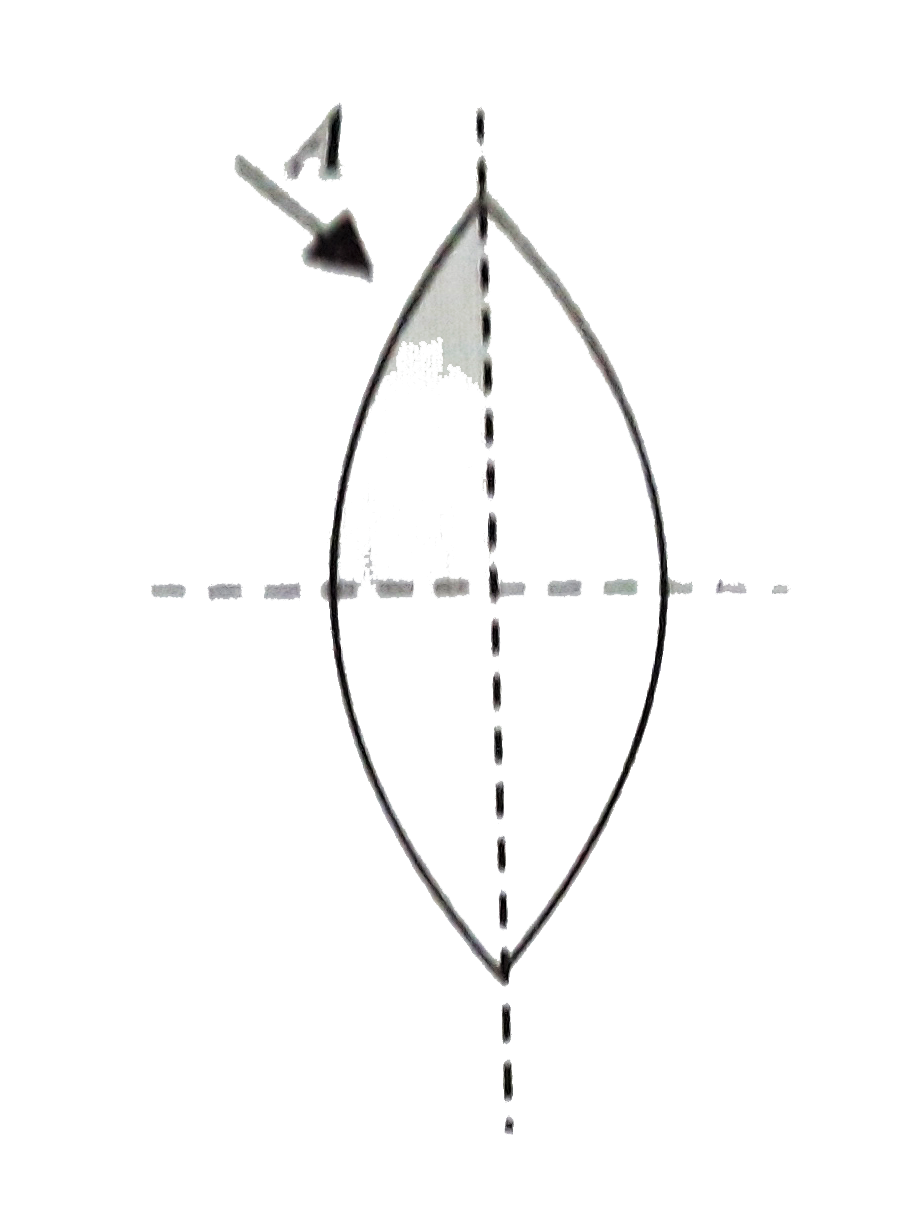 Af/2BfC4fD2f
Af/2BfC4fD2fIn the figure (i) a thin lens of focal length 10cm is shown. The lens is cut into two equal parts, and the parts are arranged as shown in the figure (ii). An object AB of height 1cm is placed at distance of 7.5cm from the arrangement. The height of the final image will be:
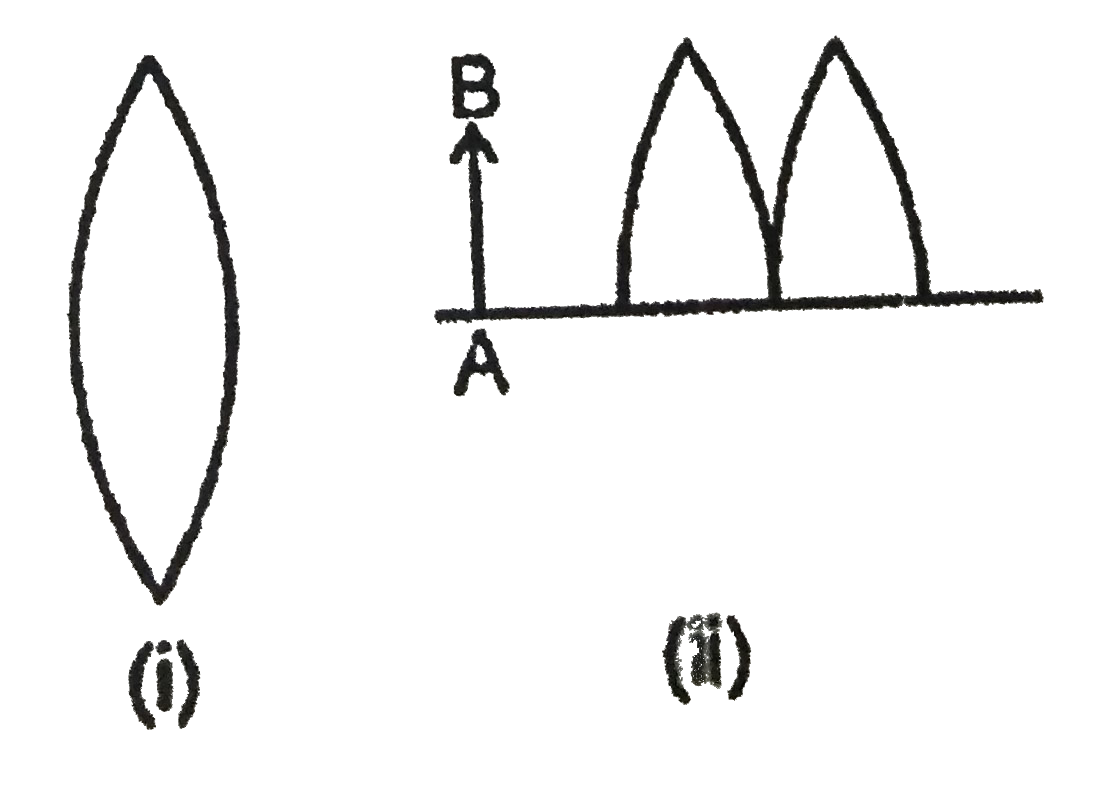 A0.5 cmB2 cmC1 cmD4 cm
A0.5 cmB2 cmC1 cmD4 cm
A convex lens has a focal length f. It is cut into two parts along the dotted line as shown in figure. The focal length of each part will be

View SolutionA convex lens has a focal length f. It is cut into two parts along the dotted line as shown in figure. The focal length of each part will be

View SolutionA thin symmetrical double convex lens of power P is cut into three parts, as shown in the figure. Power of A is

View SolutionIf a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
View SolutionA real image of a point object O was formed by an equi-convex lens of focal length f and the magnification was found to be unity. Now the lens is cut into two symmetrical pieces as shown by the dotted line and the right part is removed. The position of the image formed by the remaining part is at
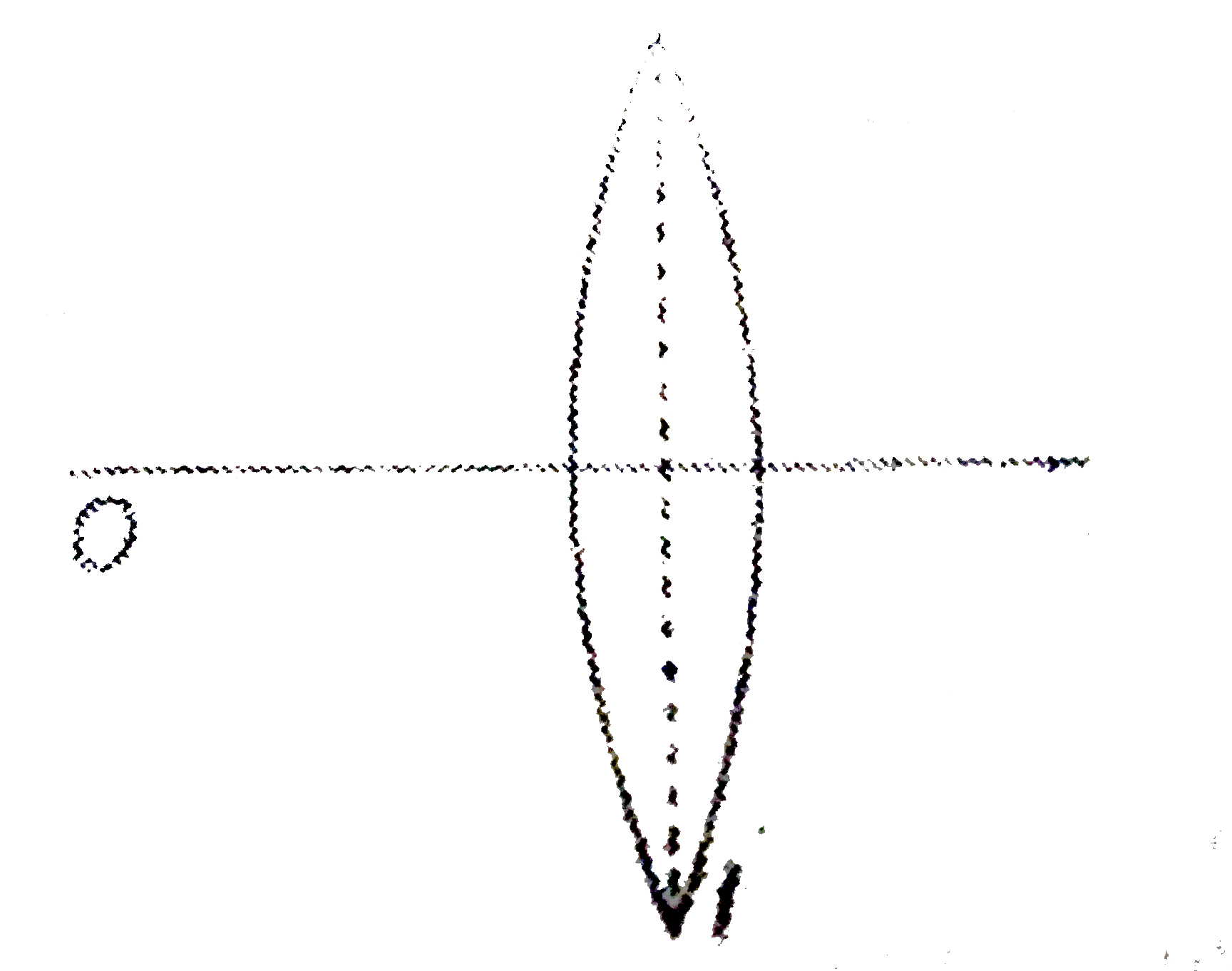
View Solution
