A pendulum of length 2 m consists of a wooden bob of mass 50 g. A bullet of mass 75 g is fired towards the stationary bob with a speed v. The bullet emerges out of the bob with a speed v3 and the bob just completes the vertical circle. The value of v is ______ ms−1 (if g=10m/s2 ).
To solve the problem, we need to analyze the situation step by step.
Step 1: Understanding the Problem
We have a pendulum with a wooden bob of mass m2=50g=0.05kg and a bullet of mass m1=75g=0.075kg that strikes the bob. The bullet enters the bob with speed v and exits with speed v3. The pendulum bob must have enough speed to complete a vertical circle after the collision.
Step 2: Applying Conservation of Momentum
Before the collision, the momentum of the system is only due to the bullet since the bob is stationary:
Initial Momentum=m1⋅v
After the collision, the momentum consists of the momentum of the bob and the bullet:
Final Momentum=m2⋅vb+m1⋅v3
where vb is the speed of the bob after the collision.
By the conservation of momentum:
m1⋅v=m2⋅vb+m1⋅v3
Step 3: Finding the Speed of the Bob
To find vb, we need to determine the speed required for the bob to complete a vertical circle. The minimum speed at the top of the circle is given by:
vtop=√g⋅L
where g=10m/s2 and L=2m:
vtop=√10⋅2=√20=2√5m/s
Using energy conservation, the speed vb at the bottom of the swing must be:
vb=√5gL=√5⋅10⋅2=√100=10m/s
Step 4: Substitute vb into the Momentum Equation
Now we substitute vb=10m/s back into the momentum equation:
m1⋅v=m2⋅10+m1⋅v3
Substituting the values:
0.075⋅v=0.05⋅10+0.075⋅v3
This simplifies to:
0.075v=0.5+0.025v
Rearranging gives:
0.075v−0.025v=0.5
0.05v=0.5
v=0.50.05=10m/s
Final Answer
The value of v is 10m/s.
---
We have a pendulum with a wooden bob of mass m2=50g=0.05kg and a bullet of mass m1=75g=0.075kg that strikes the bob. The bullet enters the bob with speed v and exits with speed v3. The pendulum bob must have enough speed to complete a vertical circle after the collision.
Before the collision, the momentum of the system is only due to the bullet since the bob is stationary:
Initial Momentum=m1⋅v
After the collision, the momentum consists of the momentum of the bob and the bullet:
Final Momentum=m2⋅vb+m1⋅v3
where vb is the speed of the bob after the collision.
m1⋅v=m2⋅vb+m1⋅v3
To find vb, we need to determine the speed required for the bob to complete a vertical circle. The minimum speed at the top of the circle is given by:
vtop=√g⋅L
where g=10m/s2 and L=2m:
vtop=√10⋅2=√20=2√5m/s
Using energy conservation, the speed vb at the bottom of the swing must be:
vb=√5gL=√5⋅10⋅2=√100=10m/s
Now we substitute vb=10m/s back into the momentum equation:
m1⋅v=m2⋅10+m1⋅v3
Substituting the values:
0.075⋅v=0.05⋅10+0.075⋅v3
This simplifies to:
0.075v=0.5+0.025v
Rearranging gives:
0.075v−0.025v=0.5
0.05v=0.5
v=0.50.05=10m/s
The value of v is 10m/s.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A
19 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A (ASSERTION (A) REASON (R))
1 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A simple pendulum of length 1m has a wooden bob of mass 1kg. It is struck by a bullet of mass 10g moving with a speed of 200m/s. The bullet gets embedded into the bob. Obtain the height to which the bob rises before swinging back.
Take g=10m/s2.
View SolutionA pendulum comsists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1 and it emerges from the bob with speed v13. The bob just completes motion along a vertical circle. Then v1 is
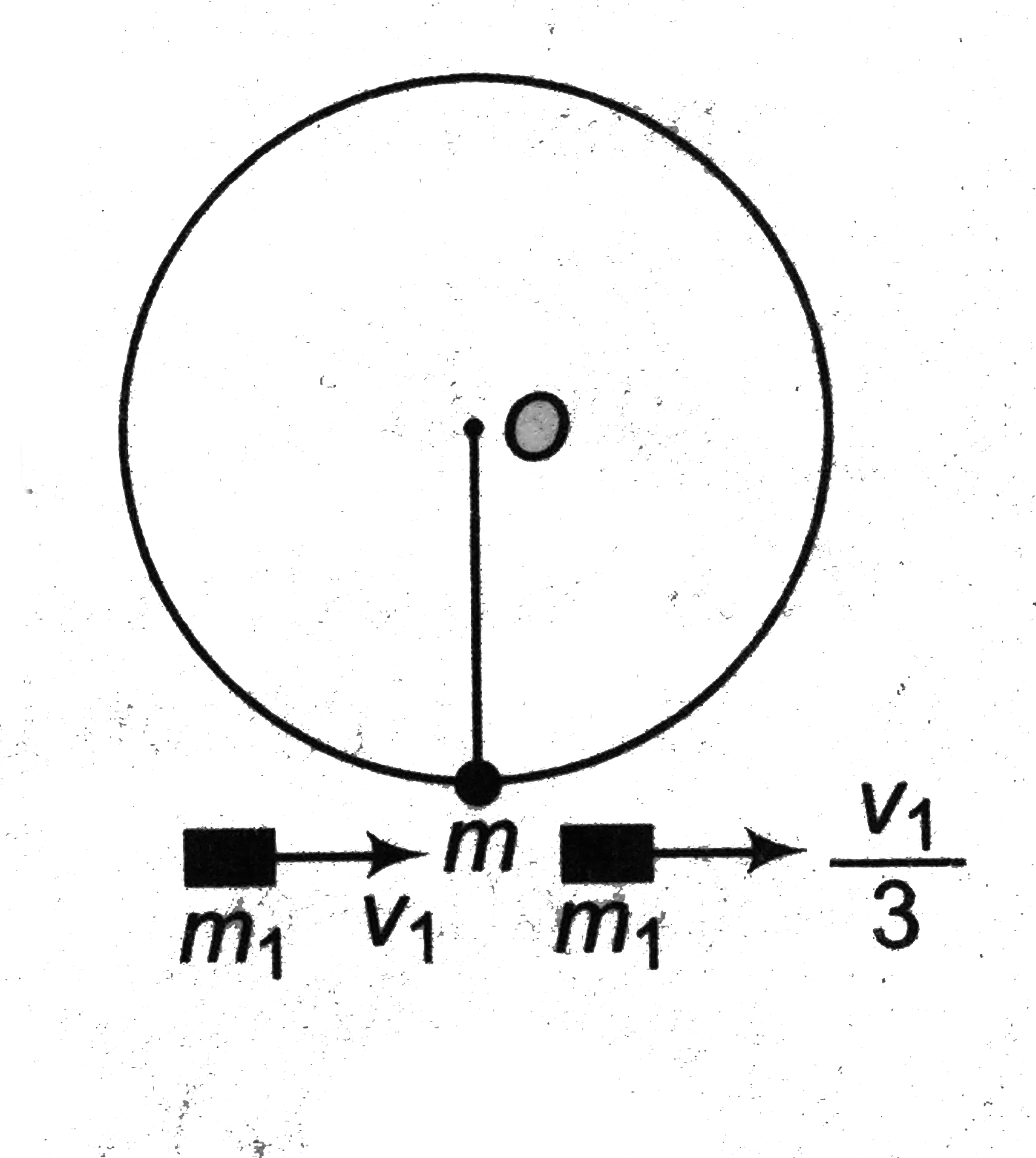
View Solution
Knowledge Check
A pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
A3m2m1√5glBm1m√5glC2m3m1√5glDm1m√glA pendulum consists of a wooden bob of mass in and of length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed (v1)/3 and the bob just completes motion along a vertical circle. Then v1is
A(mm1)√5glB32(mm1)√5glC23(m1m)√5glD(m1m)√glA pendulum consists of a wooden bob of mass m and of length L. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed v1/3 and the just completes motion along a vertical circle. Then v1 is:
A(mm1)√5glB32(mm1)√5glC23(mm1)√5glD(m1m)√gl
A pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob is just able to complete the circular motion, then tension at the lowest point just when the bob starts rising will be
View SolutionA pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
What is the momentum transferred to the bob by the bullet?
View SolutionA pendulum consists of a wooden bob of mass M and length l. A bullet of mass m is fired towards the pendulum with a speed v. The bullet emerges immediately out of the bob from the other side with a speed of v/2 and the bob starts rising. Assume no loss of mass of bob takes place due to penetration.
If the bob stops where the string becomes horizontal then v is
View SolutionA simple pendulum of length 1 m has a wooden bob of mass 1 kg. It is struck by a bullet of mass 10−2 kg moving with a speed of 2×102m/s. The bullet get embedded into the bob. Find the height to which the bob rises before swinging back.
View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View Solution
