A block of mass 200 g is kept stationary on a smooth inclined plane by applying a minimum horizontal force F=√xN as shown in figure The value of x = ______
To solve the problem, we need to analyze the forces acting on the block on the inclined plane. Here's a step-by-step solution:
Step 1: Understand the Problem
We have a block of mass m=200g=0.2kg on a smooth inclined plane at an angle θ=60∘. A horizontal force F=√xN is applied to keep the block stationary.
Step 2: Calculate the Weight of the Block
The weight W of the block can be calculated using the formula:
W=m⋅g
Assuming g=10m/s2:
W=0.2kg⋅10m/s2=2N
Step 3: Resolve the Weight into Components
The weight can be resolved into two components:
1. Parallel to the incline: W∥=W⋅sin(θ)=2⋅sin(60∘)=2⋅√32=√3N
2. Perpendicular to the incline: W_{\perpendicular} = W \cdot \cos(\theta) = 2 \cdot \cos(60^\circ) = 2 \cdot \frac{1}{2} = 1 \, \text{N}
Step 4: Analyze the Forces Acting on the Block
Since the block is stationary, the net force acting on it must be zero. We have:
- The component of the applied force F acting along the incline: F∥=F⋅cos(60∘)=F⋅12
- The component of the applied force F acting perpendicular to the incline: F_{\perpendicular} = F \cdot \sin(60^\circ) = F \cdot \frac{\sqrt{3}}{2}
Step 5: Set Up the Equations
1. For the forces along the incline:
F⋅cos(60∘)=W⋅sin(60∘)
Substituting the values:
F⋅12=√3
Thus,
F=2√3N
2. For the forces perpendicular to the incline:
N+F⋅sin(60∘)=W⋅cos(60∘)
This equation is not needed to find x, but it confirms the balance of forces.
Step 6: Relate the Force to √x
From the previous step, we found:
F=2√3N
Given F=√x, we equate:
√x=2√3
Squaring both sides gives:
x=(2√3)2=4⋅3=12
Final Answer
Thus, the value of x is:
12
We have a block of mass m=200g=0.2kg on a smooth inclined plane at an angle θ=60∘. A horizontal force F=√xN is applied to keep the block stationary.
The weight W of the block can be calculated using the formula:
W=m⋅g
Assuming g=10m/s2:
W=0.2kg⋅10m/s2=2N
The weight can be resolved into two components:
1. Parallel to the incline: W∥=W⋅sin(θ)=2⋅sin(60∘)=2⋅√32=√3N
2. Perpendicular to the incline: W_{\perpendicular} = W \cdot \cos(\theta) = 2 \cdot \cos(60^\circ) = 2 \cdot \frac{1}{2} = 1 \, \text{N}
Since the block is stationary, the net force acting on it must be zero. We have:
- The component of the applied force F acting along the incline: F∥=F⋅cos(60∘)=F⋅12
- The component of the applied force F acting perpendicular to the incline: F_{\perpendicular} = F \cdot \sin(60^\circ) = F \cdot \frac{\sqrt{3}}{2}
1. For the forces along the incline:
F⋅cos(60∘)=W⋅sin(60∘)
Substituting the values:
F⋅12=√3
Thus,
F=2√3N
N+F⋅sin(60∘)=W⋅cos(60∘)
This equation is not needed to find x, but it confirms the balance of forces.
From the previous step, we found:
F=2√3N
Given F=√x, we equate:
√x=2√3
Squaring both sides gives:
x=(2√3)2=4⋅3=12
Thus, the value of x is:
12
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A
19 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A (ASSERTION (A) REASON (R))
1 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A block is stationary on a rough inclined plane. How many forces are acting on the block?
View SolutionA block of mass 10kg is moving up on an inclined plane with constant acceleration 2ms−2 by applying a constant force F as shown in the figure. (take, g=10ms−2). If the work done on the block by applied force F in 2s is 120x N Joule then the value of N is?
View Solution
Knowledge Check
A sphere of weight W=100N is kept stationary on a rough inclined plane by a horizontal string AB as shown in figure. Then :
 Atension in th string is 100 NBnormal reaction on the sphere by the plane is 100 NCtension in the string is 1002+√3NDfore of friction on the sphere I 1002+√3N
Atension in th string is 100 NBnormal reaction on the sphere by the plane is 100 NCtension in the string is 1002+√3NDfore of friction on the sphere I 1002+√3NTwo particalA and B each of mass m are kept stationary by applying a horizontal force F=mg on partical B as show in figure .Then
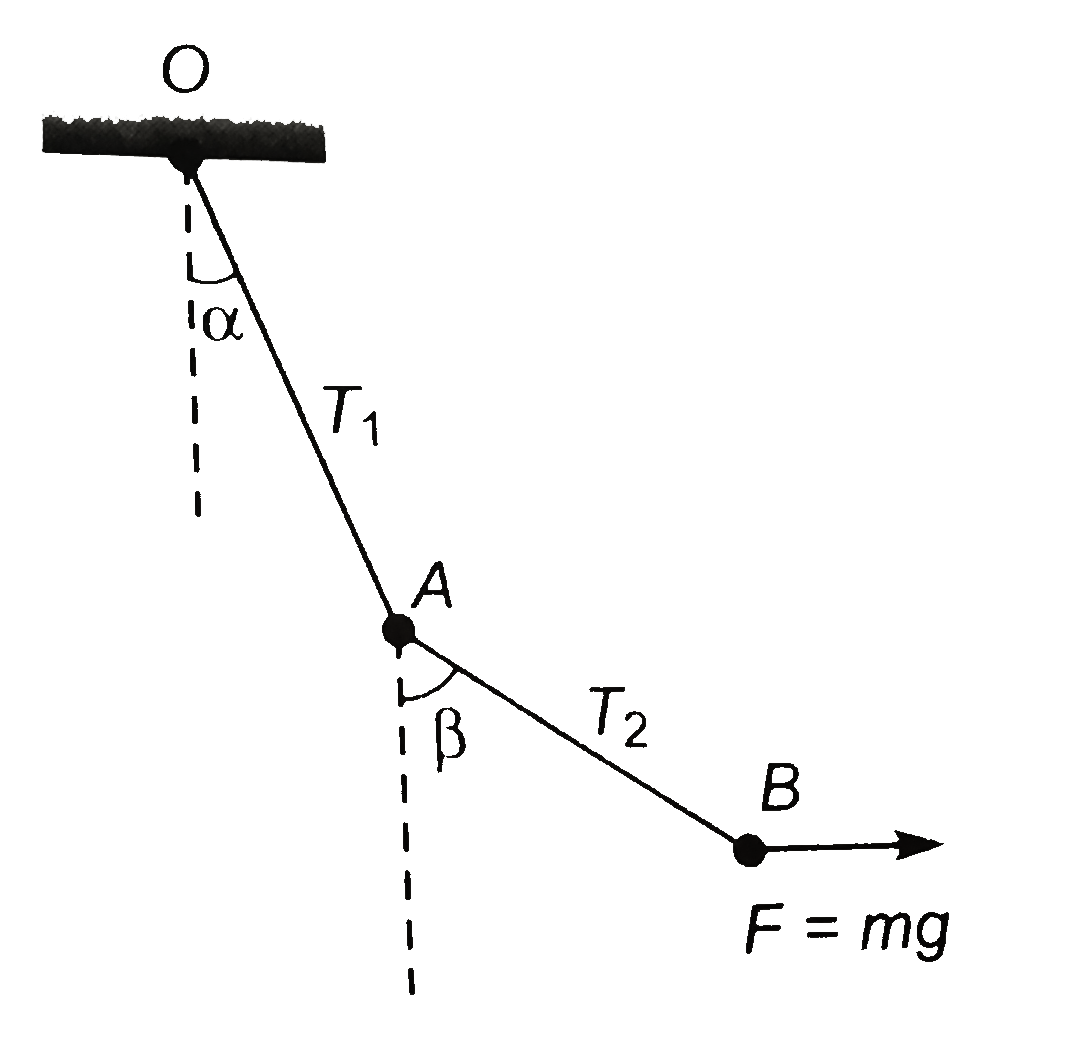 Atanβ=2tanαB2T1=5T2C√2T1=√5T2Dα=β
Atanβ=2tanαB2T1=5T2C√2T1=√5T2Dα=βA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ
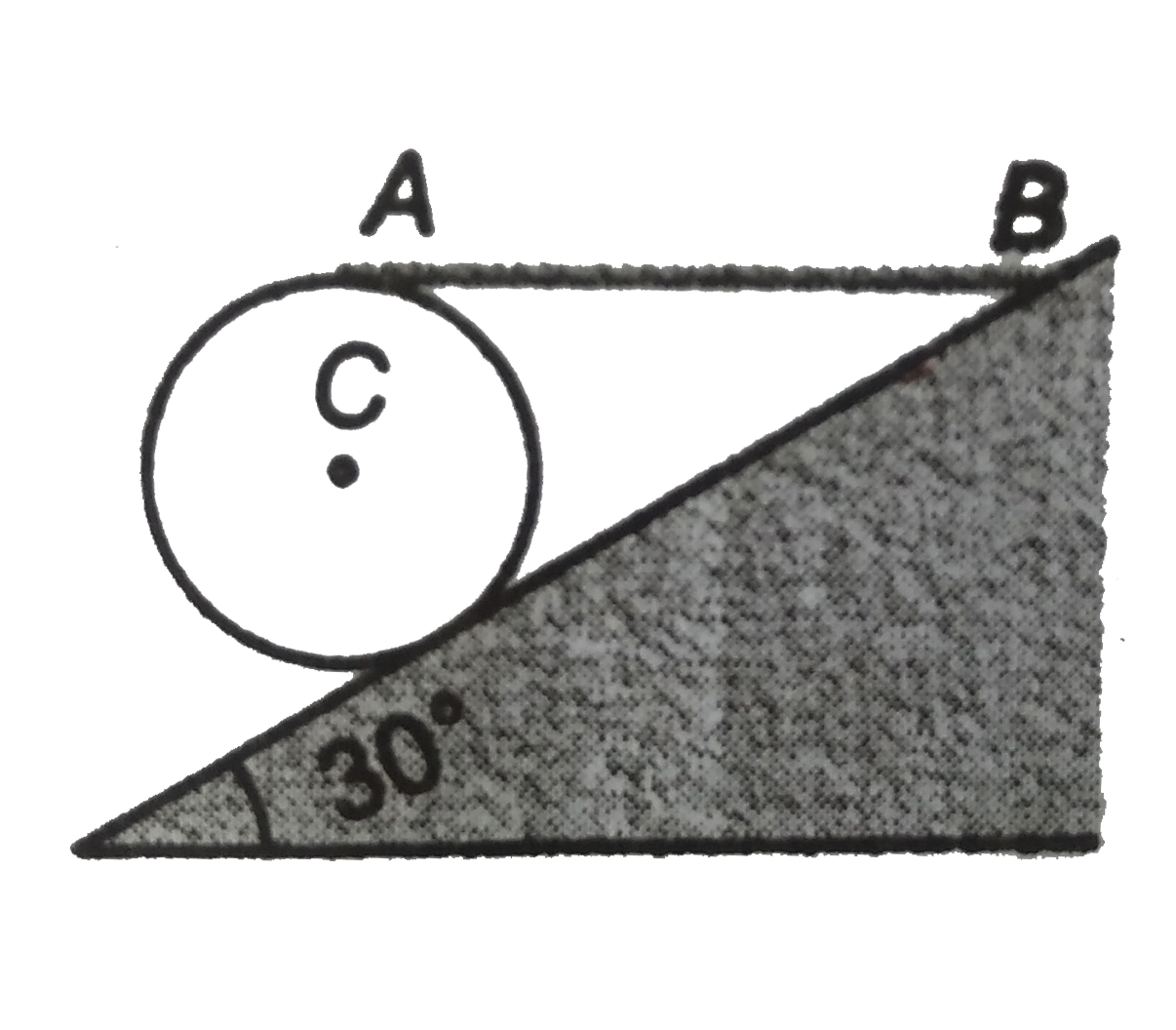
A sphere of weight w=100N is kept stationary on a rought inclined plane by a horizontal string AB as shown in figure. Find
(a)tension in the string,
(b) force of friction on the sphere and
(c)normal reation on the sphere by the plane.
View SolutionA triangular block of mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal forces F is applied to it as shown in figure below, then the correct statements is:

View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.

View SolutionA block of mass m=2kg is resting on a rough inclined plane of inclination plane of inclination 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)

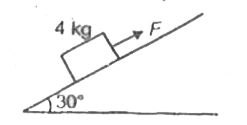
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View Solution
