A parallel beam of light is allowed to fall on a transparent spherical globe of diameter 30 cm and refractive index 1.5. The distance from the centre of the globe at which the beam of light can converge is ______ mm.
To solve the problem, we need to find the distance from the center of a transparent spherical globe where a parallel beam of light converges after passing through the globe.
1. Identify Given Values:
- Diameter of the sphere (D) = 30 cm
- Radius of the sphere (R) = D/2 = 15 cm
- Refractive index of the sphere (μ2) = 1.5
- Refractive index of air (μ1) = 1.0
2. Calculate the Image Distance from the First Surface (B1):
- Since the rays are coming from infinity, the object distance (U) is considered to be ∞.
- Using the lens maker's formula for the first surface:
μ2B1−μ1U=μ2−μ1R
- Substituting the values:
1.5B1−1∞=1.5−115
- The term 1∞ becomes 0, so:
1.5B1=0.515
- Rearranging gives:
B1=1.5×150.5=45 cm
3. Calculate the Object Distance for the Second Surface (U2):
- The distance from the center of the sphere to the first image (B1) is 45 cm, and since the radius is 15 cm, the object distance for the second surface (U2) is:
U2=R−B1=15−45=−30 cm(negative because it is on the same side as the incoming light)
4. Calculate the Image Distance from the Second Surface (B2):
- Using the lens maker's formula for the second surface:
μ1B2−μ2U2=μ1−μ2R
- Substituting the values:
1B2−1.5−30=1−1.515
- Simplifying gives:
1B2+1.530=−0.515
- This can be rewritten as:
1B2+0.051=−0.03331
- Rearranging gives:
1B2=−0.0333−0.05=−0.0833
- Thus:
B2=−12 cm
5. Calculate the Final Image Distance from the Center:
- The total distance from the center of the sphere to the final image is:
Distance from center=R+|B2|=15+12=27 cm
- Converting to mm:
27 cm=270 mm
Final Answer:
The distance from the center of the globe at which the beam of light can converge is 270 mm.
- Diameter of the sphere (D) = 30 cm
- Radius of the sphere (R) = D/2 = 15 cm
- Refractive index of the sphere (μ2) = 1.5
- Refractive index of air (μ1) = 1.0
- Since the rays are coming from infinity, the object distance (U) is considered to be ∞.
- Using the lens maker's formula for the first surface:
μ2B1−μ1U=μ2−μ1R
- Substituting the values:
1.5B1−1∞=1.5−115
- The term 1∞ becomes 0, so:
1.5B1=0.515
- Rearranging gives:
B1=1.5×150.5=45 cm
- The distance from the center of the sphere to the first image (B1) is 45 cm, and since the radius is 15 cm, the object distance for the second surface (U2) is:
U2=R−B1=15−45=−30 cm(negative because it is on the same side as the incoming light)
- Using the lens maker's formula for the second surface:
μ1B2−μ2U2=μ1−μ2R
- Substituting the values:
1B2−1.5−30=1−1.515
- Simplifying gives:
1B2+1.530=−0.515
- This can be rewritten as:
1B2+0.051=−0.03331
- Rearranging gives:
1B2=−0.0333−0.05=−0.0833
- Thus:
B2=−12 cm
- The total distance from the center of the sphere to the final image is:
Distance from center=R+|B2|=15+12=27 cm
- Converting to mm:
27 cm=270 mm
The distance from the center of the globe at which the beam of light can converge is 270 mm.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A
19 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A (ASSERTION (A) REASON (R))
1 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A narrow parallel beam of light falls on a glass sphere of radius R and refractive index μ at normal incidence. The distance of the image from the outer edge is given by-
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :

View Solution
Knowledge Check
A parallel beam of light falls on a solid tranparent sphere.
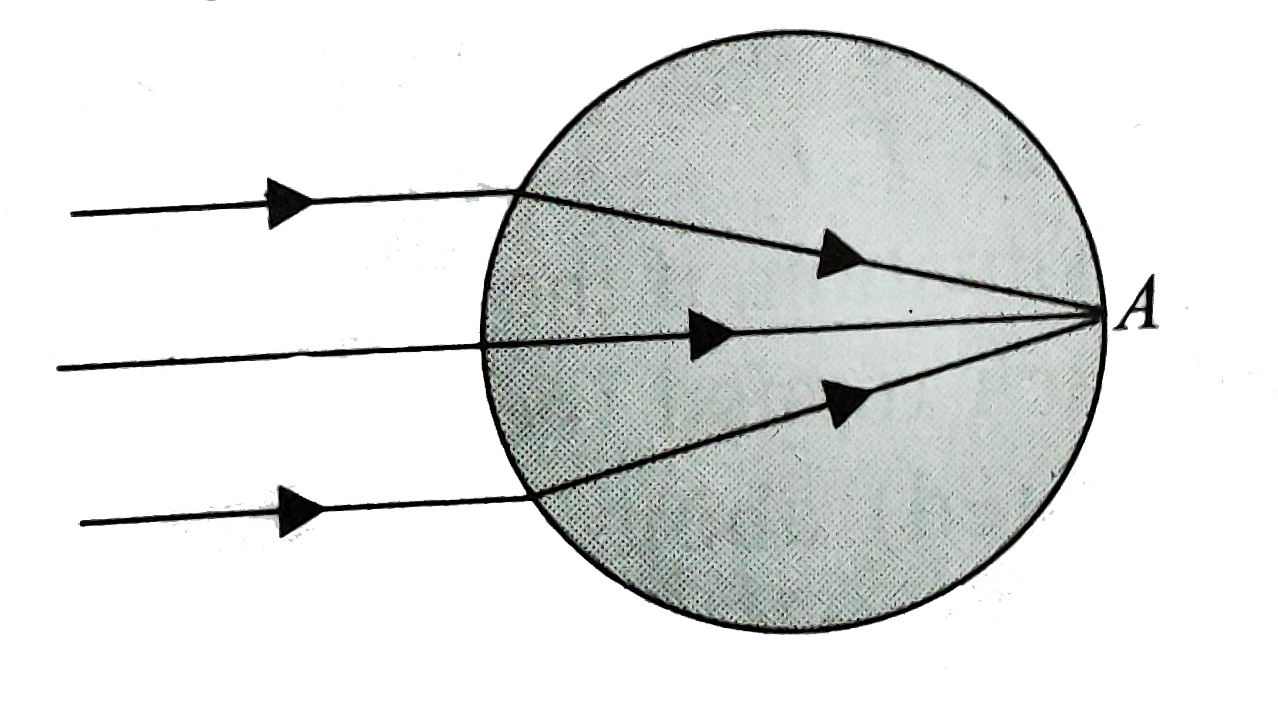
Q. Which is corret?AIf the beam is thick, then whole beam can be focussed at A.Bthe whole beam can be focussed at A only if the beam is thin enoughCif the beam is thin, then the beam can't be focussed before A.Dnone of theseA parallel beam of light falls on a solid tranparent sphere.

Q. For what value of refractive index μ, the thin beam can be focussed at centre of sphere.A1.5B2C2.5Dnone of theseA parallel beam of light falls on a solid tranparent sphere.
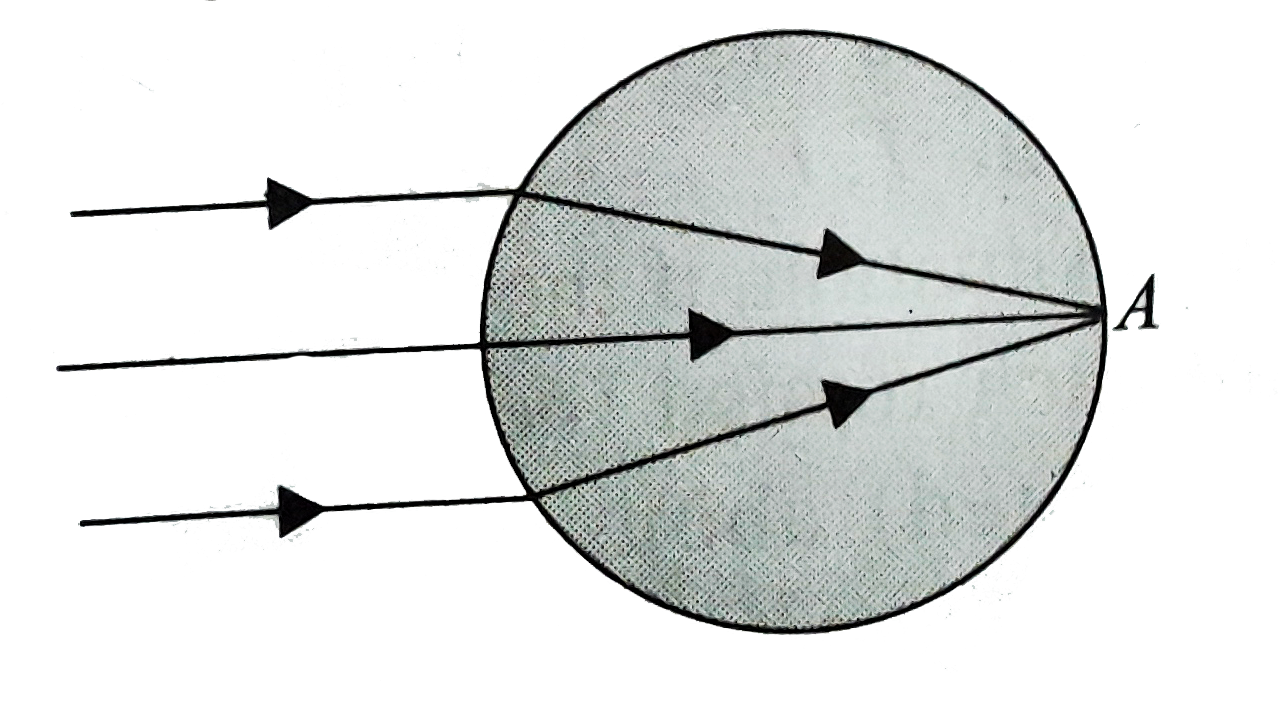
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,A1.5B1.7C2.0D2.5
A circular beam of light (diameter d) falls on a plane surface of a liquid. The angle of incidence is 45∘ and refractive index of the liquid is μ. The diameter of the refracted beam is
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
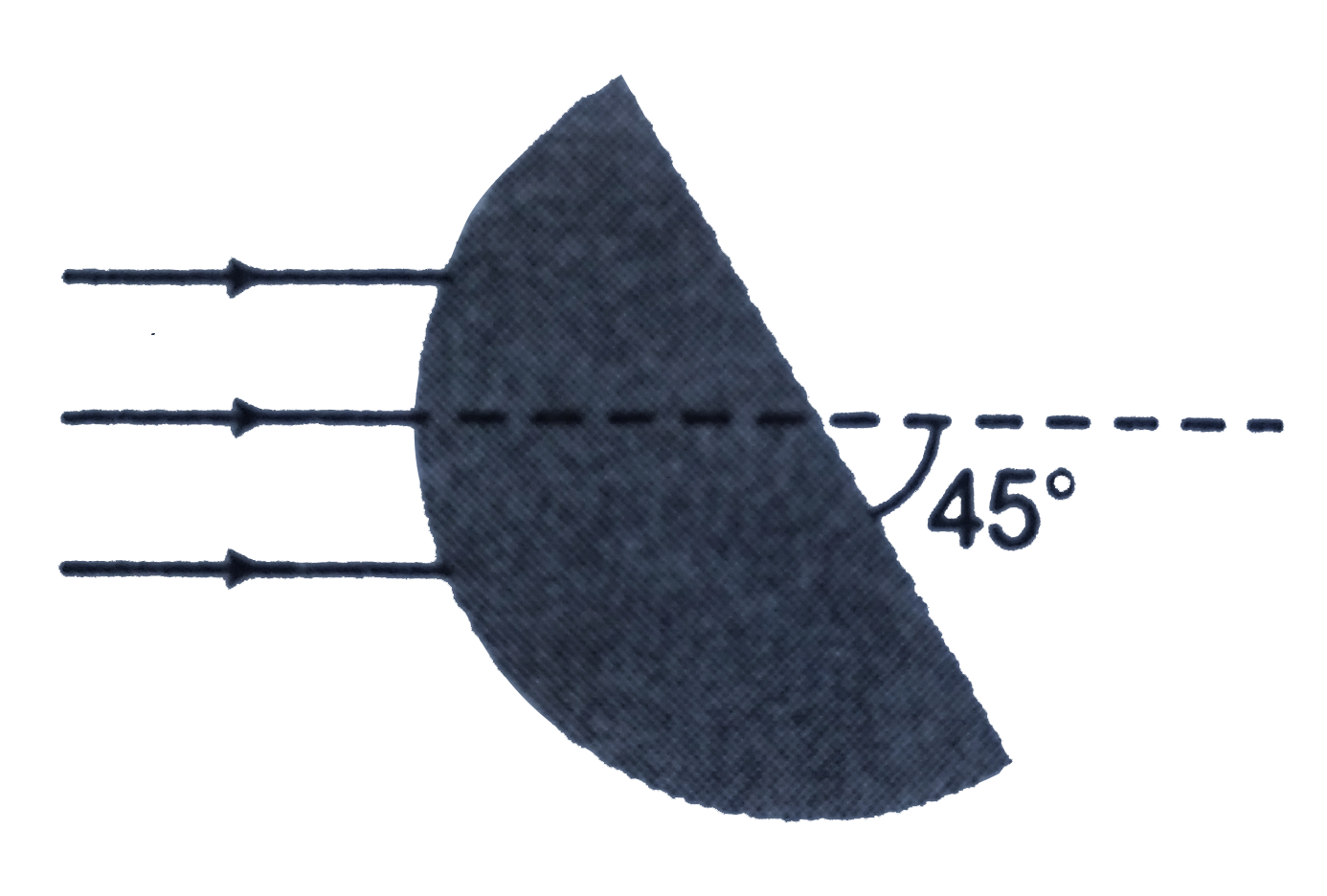
View SolutionWhen a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light, the optical path is
View SolutionAN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
View SolutionA parallel beam of light falling on the eye gets focused on the retina because of refractions at
View Solution
