A long cylindrical volume contains a uniformly distributed charge of density ρ. The radius of cylindrical volume is R. A charge particle (q) revolves around the cylinder in a circular path. The kinetic energy of the particle is :
ρqR24ε0
ρqR22ε0
qρ4ε0R2
4ε0R2qρ
To solve the problem, we need to find the kinetic energy of a charged particle q revolving around a long cylindrical volume with a uniform charge density ρ and radius R.
1. Determine the Total Charge in the Cylinder:
The volume V of the cylinder can be expressed as:
V=πR2L
where L is the length of the cylinder. The total charge Q in the cylinder is given by:
Q=ρV=ρπR2L
2. Find the Linear Charge Density:
The linear charge density λ (charge per unit length) is:
λ=QL=ρπR2LL=ρπR2
3. Calculate the Electric Field Outside the Cylinder:
For a point outside the cylinder (where the distance r from the axis of the cylinder is greater than R), the electric field E can be treated as that of a line charge:
E=2kλr
Substituting λ:
E=2k(ρπR2)r
where k=14πϵ0.
4. Express the Electric Field in Terms of ϵ0:
Substituting k:
E=2⋅14πϵ0⋅(ρπR2)r=ρR22ϵ0r
5. Set Up the Force Equation:
The electrostatic force F acting on the charge q is:
F=qE=q⋅ρR22ϵ0r
This force provides the necessary centripetal force for the particle moving in a circular path:
F=mv2r
6. Equate the Forces:
Setting the electrostatic force equal to the centripetal force:
q⋅ρR22ϵ0r=mv2r
7. Solve for mv2:
Multiplying both sides by r gives:
q⋅ρR22ϵ0=mv2
8. Calculate the Kinetic Energy:
The kinetic energy K of the particle is given by:
K=12mv2
Substituting mv2:
K=12⋅(q⋅ρR22ϵ0)=qρR24ϵ0
Final Result:
The kinetic energy of the charged particle is:
K=qρR24ϵ0
The volume V of the cylinder can be expressed as:
V=πR2L
where L is the length of the cylinder. The total charge Q in the cylinder is given by:
Q=ρV=ρπR2L
The linear charge density λ (charge per unit length) is:
λ=QL=ρπR2LL=ρπR2
For a point outside the cylinder (where the distance r from the axis of the cylinder is greater than R), the electric field E can be treated as that of a line charge:
E=2kλr
Substituting λ:
E=2k(ρπR2)r
where k=14πϵ0.
Substituting k:
E=2⋅14πϵ0⋅(ρπR2)r=ρR22ϵ0r
The electrostatic force F acting on the charge q is:
F=qE=q⋅ρR22ϵ0r
This force provides the necessary centripetal force for the particle moving in a circular path:
F=mv2r
Setting the electrostatic force equal to the centripetal force:
q⋅ρR22ϵ0r=mv2r
Multiplying both sides by r gives:
q⋅ρR22ϵ0=mv2
The kinetic energy K of the particle is given by:
K=12mv2
Substituting mv2:
K=12⋅(q⋅ρR22ϵ0)=qρR24ϵ0
The kinetic energy of the charged particle is:
K=qρR24ϵ0
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)20videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)10videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS60videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )10videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question360videos
JEE MAINS 2023 JAN ACTUAL PAPER
Similar Questions
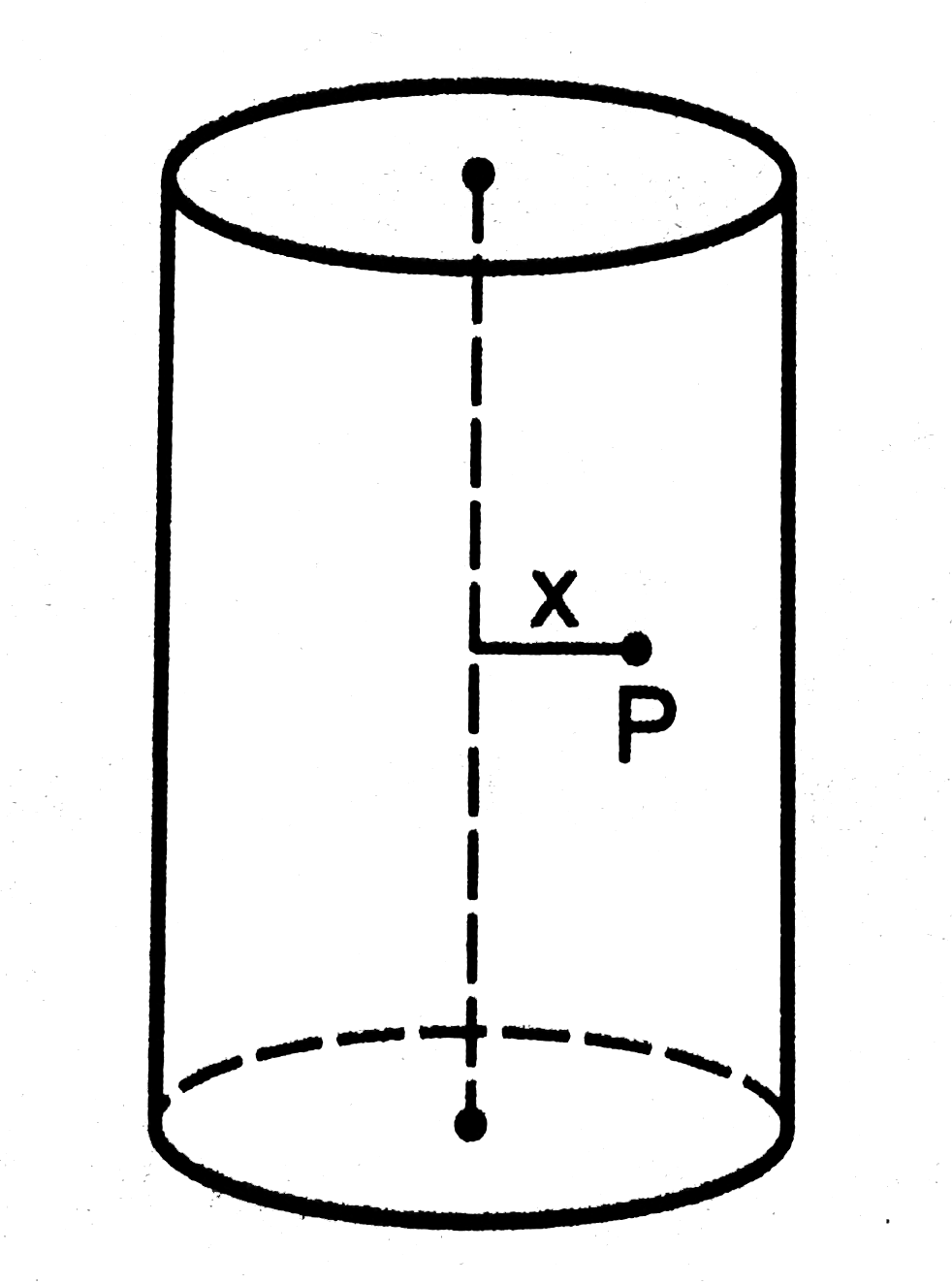
A long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
 View Solution
View SolutionA uniformly charged (linear charge density a) very long wire in placed fixed. A negative charge particle - of mass m revolves around this wire in a circular path of radius then +++++++ m
View Solution
Knowledge Check
- Question 1 - Select One or More
A long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :
 Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>R
Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>R - Question 2 - Select One
Inside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
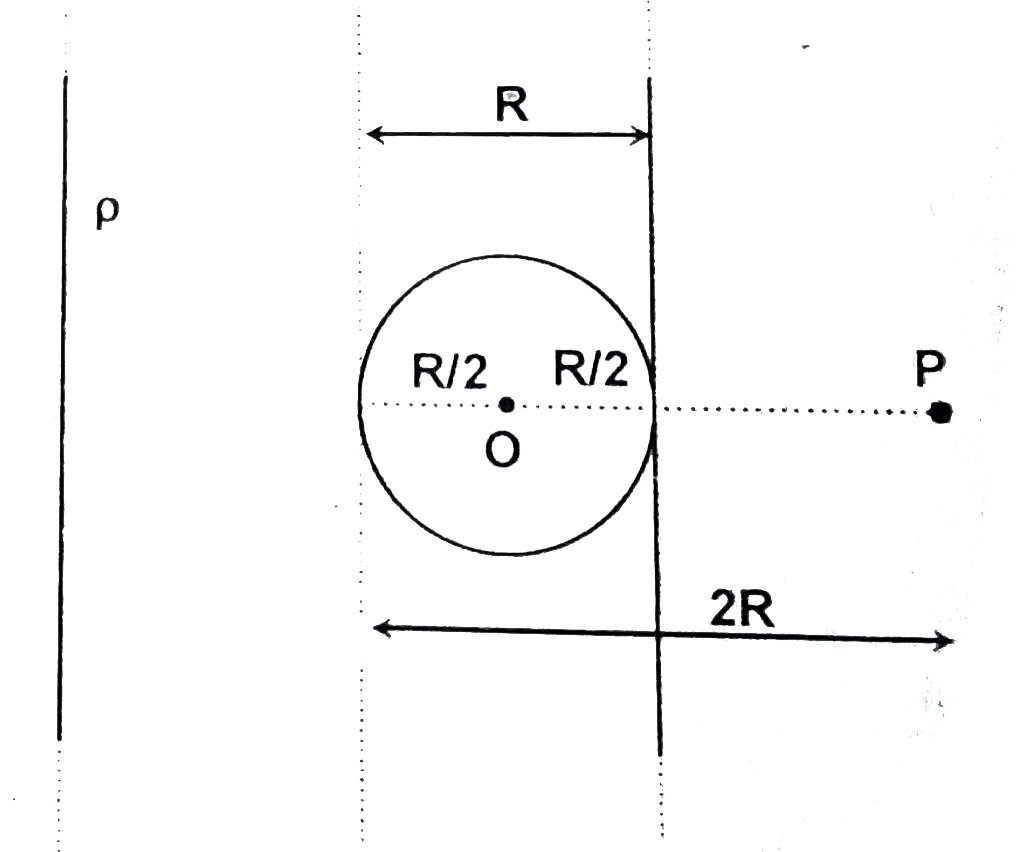 A23rhpR54ɛ0B23rhpR108ɛ0C25ρR54ɛ0D25ρR108ɛ0
A23rhpR54ɛ0B23rhpR108ɛ0C25ρR54ɛ0D25ρR108ɛ0 - Question 3 - Select One
Figure shows two large cylindrical shells having uniform linera charge densities +λ and −λ. Radius of inner cylinder is 'a' and that of outer cylinder is 'b'. A charged particle of mass m, charge q revolves in a circle of radius r. Then, its speed 'v' is : (Neglect gravity and assume the radii of both the cylinders to be very small in comparison to their length.)
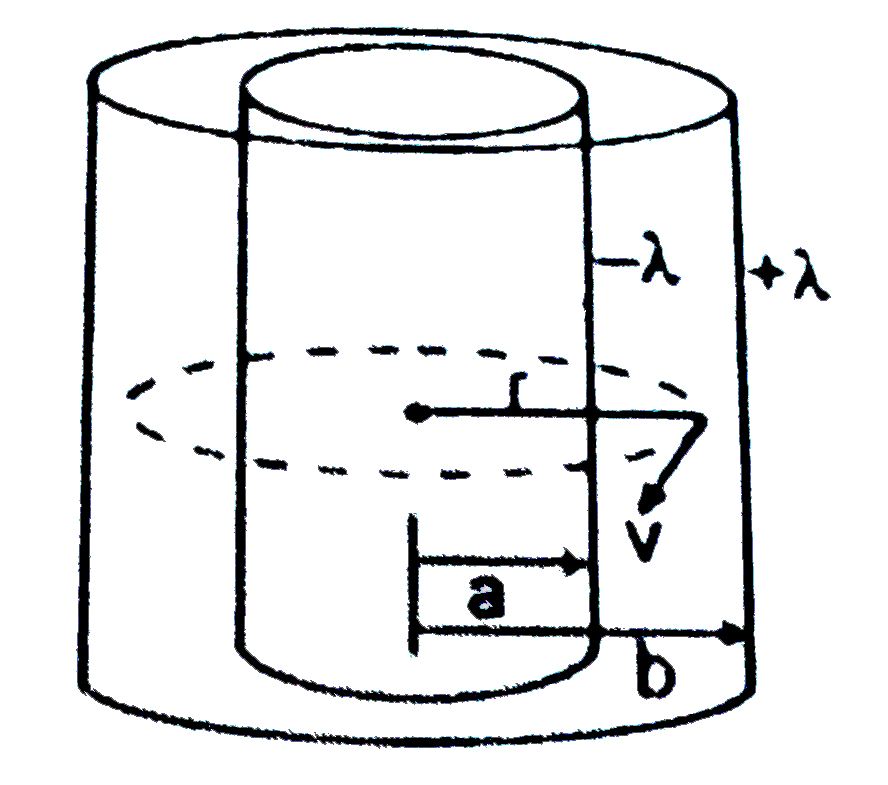 A√λq2π∈0mB√2λqπ∈0mC√λqπ∈0mD√λq4πε0m
A√λq2π∈0mB√2λqπ∈0mC√λqπ∈0mD√λq4πε0m
A long cylindrical wire carries a positive charge of linear density λ. An electron (−e,m) revolves around it in a circular path under the influence of the attractive electrostatic force. Find the speed of the electron.
View SolutionA long cylindrical wire carries a positive charge of linear density 2.0 xxx 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attactive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
View SolutionA solid non-conducting hemisphere ofradius R has' a uniformly distributed positive charge of density p per unit volume. A negatively charged particle having charge q is transferred from centre of its base to infinity. Calculate workperformed.in the processc Di-electric constant of material of hemisphere is unity:
View SolutionA small point mass m is to be thrown with such a speed at a distance x from the axis of a long cylinder of radius R and density ρ, so that m starts revolving around the cylinder in a circular orbit of radius x with centre on the axis of cylinder. Find the speed with which point mass is thrown.
View SolutionThe radius of circular path for a charged particle of mass 'm' having charge q and kinetic energy K in a uniform , normal magnetic field B is ………………… .
View Solution

