AABC is inscribed in a circle. Point P lies on a circumscribed circle of a triangle be such that through point P. PN, PM and PL are perpendicular on sides of triangle (possibly by increasing sides). Prove that points N, M and L are collinear.
Step by step video & image solution for AABC is inscribed in a circle. Point P lies on a circumscribed circle of a triangle be such that through point P. PN, PM and PL are perpendicular on sides of triangle (possibly by increasing sides). Prove that points N, M and L are collinear. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle of radius 10 cm has an equilateral triangle inscribed in it. The length of the perpendicular drawn from the centre to any side of the triangle is
A2.5√3 cmB5 cmC10√3 cmDNone of these
If a triangle is inscribed in a circle, then prove that the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the thrid side from the opposite vertex.
View SolutionIf a triangle is inscribed in a circle, then prove that the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the thrid side from the opposite vertex.
View SolutionA point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
View SolutionA point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
View SolutionA point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
View SolutionThe point of concurrence of perpendicular bisectros of the sides of a triangle is called _________
View SolutionIn the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x.
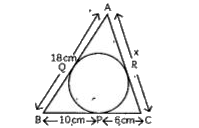 View Solution
View Solution

