ABCD is a rectangle. The line through C perpendicular to AC meets AB produced at X and AD produced at Y. Prove that the points D, B, X, Y are concyclic.
Step by step video & image solution for ABCD is a rectangle. The line through C perpendicular to AC meets AB produced at X and AD produced at Y. Prove that the points D, B, X, Y are concyclic. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
ABCD is a trapezium with AB∣∣DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

View SolutionThe side BC of a triangle ABC is bisected at D;O is any point in AD.BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FE∣∣BC.
View SolutionLet A be any point on the x-axis and B=(2,3). The perpendicular at A to the line AB meets the y-axis at C. Then the locus of midpoint of segment AC as A moves is given by
View SolutionIn the parallelogram ABCD, the line drawn through Q point P on AB, parallel to BC meets AC at Q. The line through Q, parallel to AB meets AD R.
Prove that
APPB=ARRD.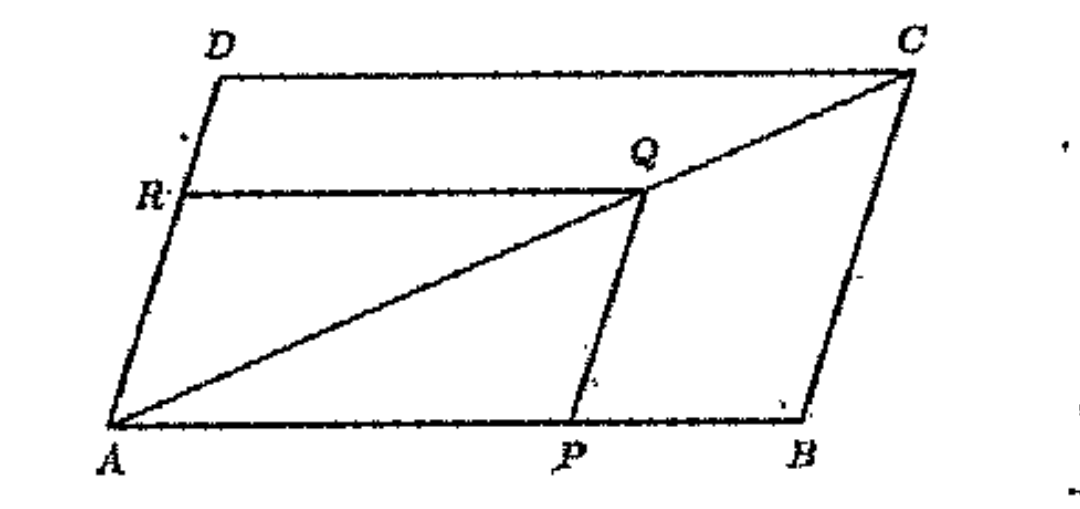 .
.
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
3DF=EF
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
4CR=AB
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawr parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that:
2×AD=GC
View Solution
