The mass of the part of the string below A i figure is m. Find the tension of he string at the lowere end and at A.
To get the tension at the lower end we need the force exerted by the string on the block.
Take block as the system. The forces on it are
a. pull of the string T, upward
b. pull of the earth Mg, downward,
The free body diagram for the block is shown in ure. s the acceleration of theblocfk is zero, these forces should add to zero. Hence the tension at the lower end is T=Mg.

To get the tension T at A we need the force exerted by the upper part of the string on the lower part of the string. For this we many write the equation of motion for the lower part of the string. So take the string below A as the system. The forces acting on this part of the string
a. T', upward by the upper pasrt of the string
b. mg, downward by the block.
c. T, downward by the block
Note that c we have written T for by the block on the string. We have already used the symbol T Newton's third law here. Teh force exerted by the block on the string is equal in magnitude to the force exerted by the string on the block.
The free body diagram for this part is hsown in ure part of the string) is an equilibrium, Newton's first law gives
T'T+mg
ButT=Mghence,T'=(M+m)g
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Worked Out Examples
11 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Short Answer
17 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA mass m is revolving in a vertical circle at the end of a string of length 20 cm. By how much does the tension of the string at the lowest point exceed the tension at the top most point?
A2 mgB4 mgC6 mgD8 mg
Find the tension in the strings AC and BC shown in figure.
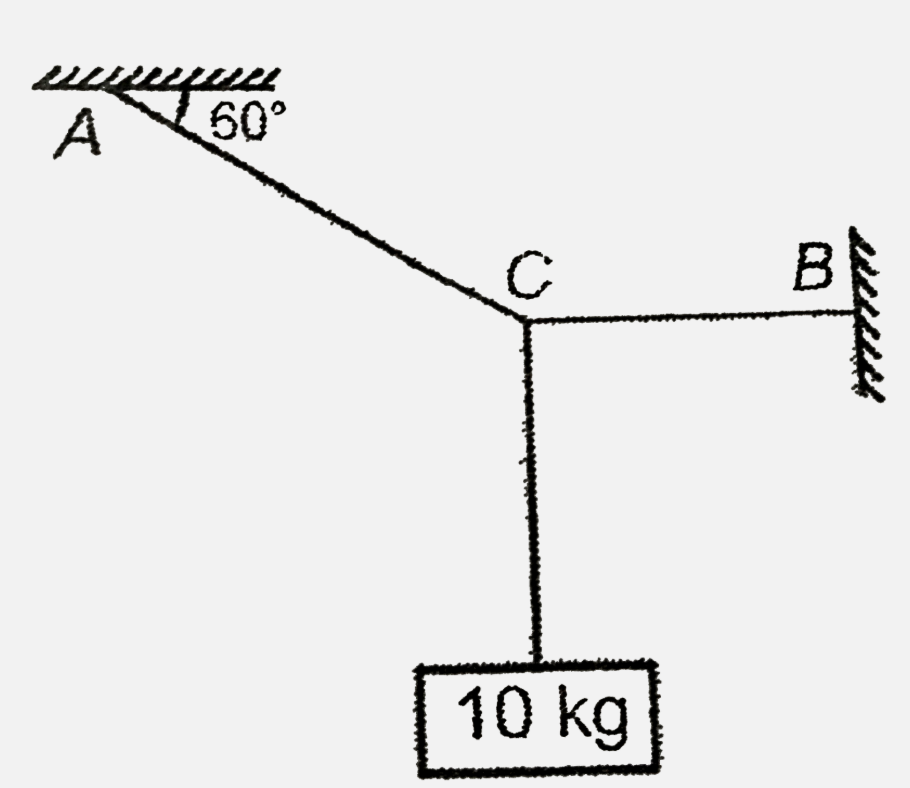
View SolutionFind the tension in the strings AC and BC shown in figure.

View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA thin uniform bar of mass m and length 2L is held at angle 30∘ with the horizontal by means of two vertical inextensible strings, at each and as shown in figure. If the string at the right end breaks, leaving the bar to swing the tension in the string at the left end of the bar immediately after string breaks is T=n13mg

View SolutionA bob of weight 3N is in equilibrium under the action of two string 1 and 2 (figure) . Find the tension forces in the string.
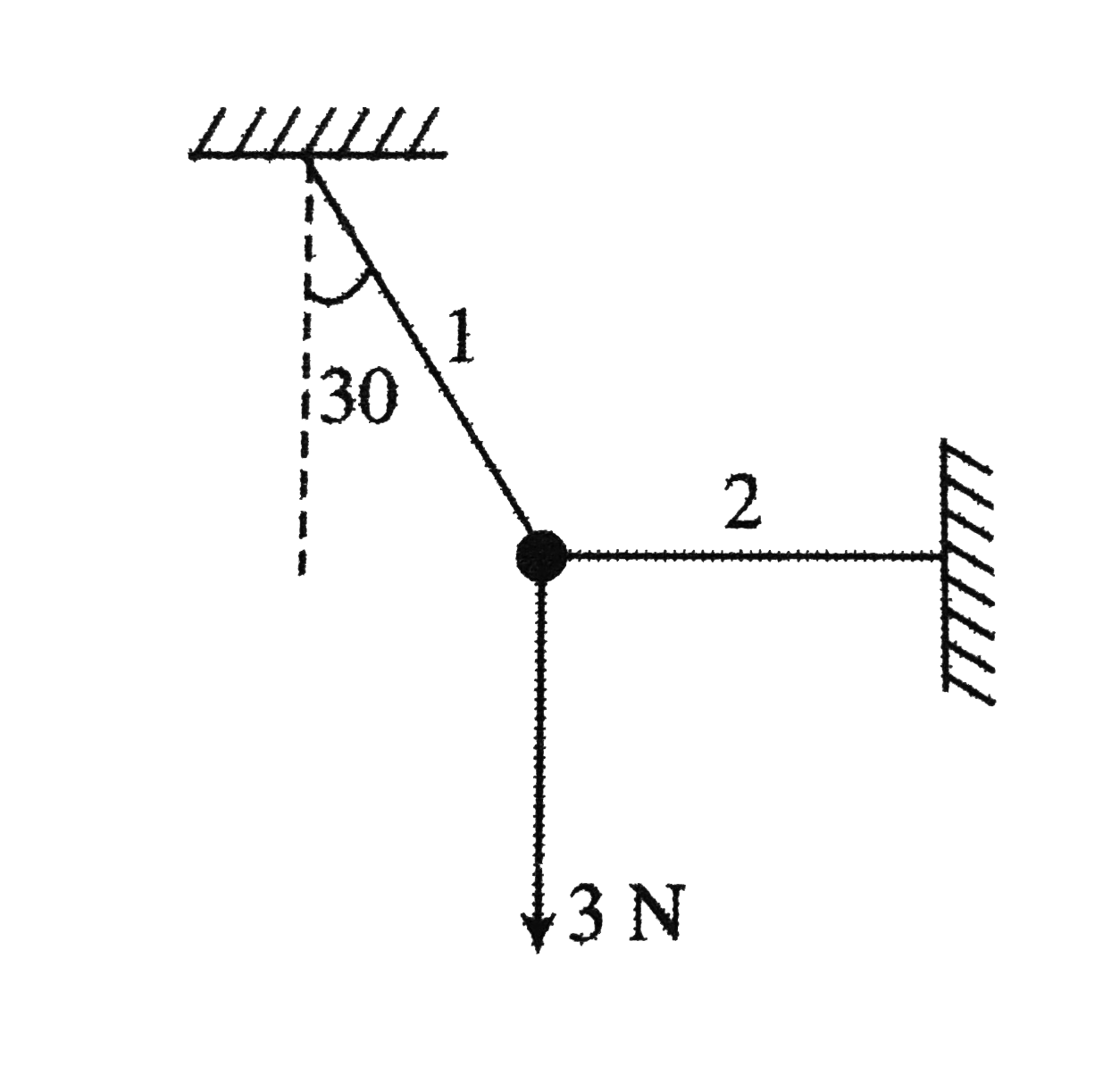
View SolutionFor the system shown in figure, the tensions in the string
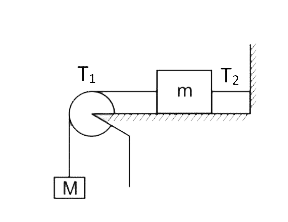
View Solution


