Using the formula for the moment of inertia of a uniform sphere, find the moment of inertia of a thin spherical layer of mass m and radius R relative to the axis passing through its centre.
Moment of inertia of the shaded portion, about the axis passing through it's centre,
I=25(43πR3ρ)R2−25(43πr3ρ)r3
=25⋅43πρ(R5−r5)
Now, if R=r+dr, the shaded portion becomes a shell, which is the required shape to calculate the moment of inertia.
Now, I=25−43πρ{(r+dr)5−r5}
=25⋅43πρ(r5+5r4dr+........−r5)
Neglecting higher terms.
=23(4πr2drρ)r2=23mr2

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
Find the moment of inertia of a pair of spheres, each having a mass m and radius r kept in contact about the tangent passing through the point of contact.
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a sphere of radius R about an axis passing through its centre is proportional to-
AR2BR3CR4DR5 - Question 2 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2 - Question 3 - Select One
The curve for the moment of inertia of a sphere of constant mass M versus its radius will be:
A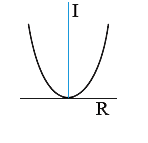 B
B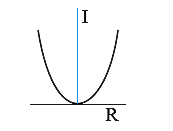 C
C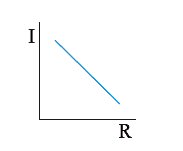 D
D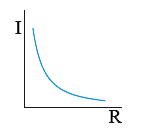
Find the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.
 View Solution
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionFind moment of inertia of a uniform solid sphere (mass m, radius r) about a tangent.
View SolutionMoment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
View Solution

