A particle goes in a circle of radius 2.0 cm. A concave mirror of focal length 20 cm is placed with its principal axis passing through the centre of the circle and perpendicular to its plane. The distance between the pole of the mirror and the centre of the circle is 30 cm. Calculate the radius of the circle formed by the image.
Video Solution
Text Solution
u = -30 cm,
f= -20 cm
We know, 1υ+1υ=1f
⇒=1υ+−130=−120
⇒1υ=130−120=160
⇒υ=60cm
Image of the circle is formed at a distance 60 cm in front of the mirror.
∴m=−υu=Rima≥Robject
⇒−(−60)(−30)υ=Rima≥2
⇒Rima≥=4cm
Radius of image of the circle is 4 cm.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two circles touch each other externally. The distance between their centres is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
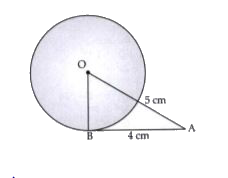
A3.5cmB3cm.C4cmD2cmThe distance of point A from the centre of the circle is 5 cm. The length of the tangent is 4 cm. The radius of the circle is :
A3 cmB4 cmC5 cmD8 cmTwo circles touch each other externally. The distance between their centres is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
A3.5 cmB3 cmC4 cmD2 cm
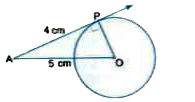
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionThe length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
View SolutionIf area of sector of a circle is 105cm2 and length of its arc is 30cm, calculate the radius the circle
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.
View SolutionThe length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
View Solution