monatomic ideal gas is contained in a rigid container of volume V with walls of totsl inner surface area A, thickness x and thermal condctivity K. The gas is at an initial temperature t0 and pressure P0 . Find tjr pressure of the gas as a function of time if the temperature of the surrounding air is Ts . All temperature are in absolute scale.
To find the pressure of a monatomic ideal gas as a function of time in a rigid container, we can follow these steps:
Step 1: Understand the System
We have a monatomic ideal gas in a rigid container with:
- Volume V (constant)
- Inner surface area A
- Thickness x
- Thermal conductivity K
- Initial temperature T0
- Initial pressure P0
- Surrounding temperature Ts
Step 2: Heat Transfer to the Gas
Since the container is rigid, the volume of the gas remains constant. The heat ΔQ absorbed by the gas can be expressed in terms of the change in temperature ΔT:
ΔQ=Cv⋅n⋅ΔT
For a monatomic ideal gas, the molar heat capacity at constant volume Cv is given by:
Cv=32R
Assuming we have 1 mole of gas (n=1):
ΔQ=32RΔT
Step 3: Heat Current
The heat current into the gas can be expressed using Fourier's law of heat conduction:
ΔQΔt=KA(Ts−T)x
where T is the temperature of the gas at time t.
Step 4: Relate ΔQ and Heat Current
We can equate the two expressions for heat:
32RΔTΔt=KA(Ts−T)x
This can be rearranged to:
ΔTΔt=2KA(Ts−T)3Rx
Step 5: Integrate the Equation
We need to integrate this equation. The temperature changes from T0 to T as time changes from 0 to t:
∫TT01Ts−T′dT′=−2KA3Rx∫t0dt′
This gives us:
ln(Ts−T)−ln(Ts−T0)=−2KA3Rxt
Simplifying, we have:
ln(Ts−TTs−T0)=−2KA3Rxt
Step 6: Solve for T
Exponentiating both sides:
Ts−TTs−T0=e−2KA3Rxt
Rearranging gives:
Ts−T=(Ts−T0)e−2KA3Rxt
Thus, we find:
T=Ts−(Ts−T0)e−2KA3Rxt
Step 7: Relate Pressure to Temperature
Using the ideal gas law, since the volume is constant, we can relate the pressure and temperature:
PT=P0T0
Thus, the pressure P can be expressed as:
P=P0TT0
Substituting for T:
P=P0Ts−(Ts−T0)e−2KA3RxtT0
Final Expression for Pressure
The final expression for the pressure of the gas as a function of time is:
P(t)=P0Ts−(Ts−T0)e−2KA3RxtT0
---
We have a monatomic ideal gas in a rigid container with:
- Volume V (constant)
- Inner surface area A
- Thickness x
- Thermal conductivity K
- Initial temperature T0
- Initial pressure P0
- Surrounding temperature Ts
Since the container is rigid, the volume of the gas remains constant. The heat ΔQ absorbed by the gas can be expressed in terms of the change in temperature ΔT:
ΔQ=Cv⋅n⋅ΔT
For a monatomic ideal gas, the molar heat capacity at constant volume Cv is given by:
Cv=32R
Assuming we have 1 mole of gas (n=1):
ΔQ=32RΔT
The heat current into the gas can be expressed using Fourier's law of heat conduction:
ΔQΔt=KA(Ts−T)x
where T is the temperature of the gas at time t.
We can equate the two expressions for heat:
32RΔTΔt=KA(Ts−T)x
This can be rearranged to:
ΔTΔt=2KA(Ts−T)3Rx
We need to integrate this equation. The temperature changes from T0 to T as time changes from 0 to t:
∫TT01Ts−T′dT′=−2KA3Rx∫t0dt′
This gives us:
ln(Ts−T)−ln(Ts−T0)=−2KA3Rxt
Simplifying, we have:
ln(Ts−TTs−T0)=−2KA3Rxt
Exponentiating both sides:
Ts−TTs−T0=e−2KA3Rxt
Rearranging gives:
Ts−T=(Ts−T0)e−2KA3Rxt
Thus, we find:
T=Ts−(Ts−T0)e−2KA3Rxt
Using the ideal gas law, since the volume is constant, we can relate the pressure and temperature:
PT=P0T0
Thus, the pressure P can be expressed as:
P=P0TT0
Substituting for T:
P=P0Ts−(Ts−T0)e−2KA3RxtT0
The final expression for the pressure of the gas as a function of time is:
P(t)=P0Ts−(Ts−T0)e−2KA3RxtT0
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Short Answer
11 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Objective 1
10 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View SolutionIn the show indicator diagram over pressure - volume scales 'n' moles of an ideal gas is cycled . If the temperature of the gas in the state X and Y are respectively TXandTY . Temperature of the gas in the state Z is the (All temperature are in absolute scale )
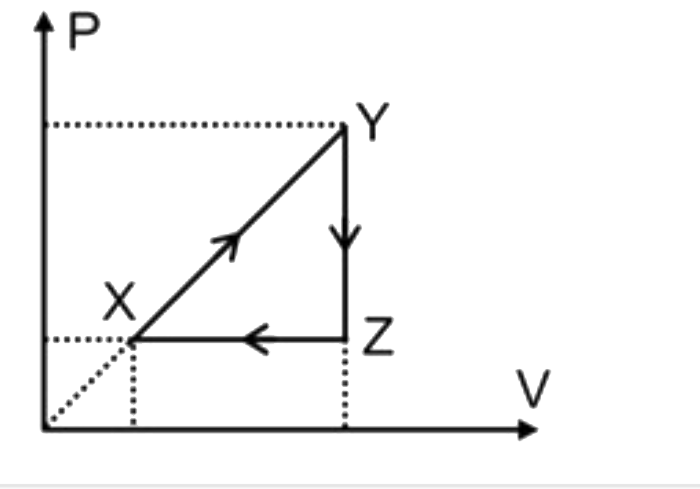
View Solution
Knowledge Check
A gas is found to obey the law P2V=constant. The initial temperature and volume are T0andV0. If the gas expands to a volume 3V0, its final temperature becomes
AT03BT0√3C3T0D√3T0A gas is found to obey the law p2V = constant. The initial temperature and volume are T0 and V0 . If the gas expands to a volume 3V0, its final temperature becomes
AT03BT0√3C√3T0DNone of theseA gas is found to obey the law P2V= constant. The initial temperature and volume are T0 and V0∘ If the gas expands to a volume 3V0, then
A√3T0B√2T0CT0√3DT0√2
A quantity of gas occupies an initial volume V0 at pressure p0 and temperature T0. It expands to a volume V (a) constant temperature and (b) constant pressure. In which case does the gas do more work ?

View SolutionDuring an experiment, an ideal gas is found to obey a condition Vp2= constant. The gas is initially at a temperature (T), pressure (p) and volume (V). The gas expands to volume (4V).
View SolutionOne mole of monatomic gas is brought from state A to state B. The initial temperature at A is T0. The temperature at B will be –

View SolutionIf the temperature of a gas is increased by 1K at constant pressure its volume increase by 0.0035 of the initial volume. The temperature of the gas is
View SolutionA uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
View Solution
