Prove that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
Let ABC be a triangle and N be the midpoints of the sides AB and AC.
then we have to show that MN is parallel to BC and
l(MN)=12⋅l(BC).
Let ¯a,¯b,¯c,¯¯¯mand¯n be the position
vectors of A,B,C, M and N respectively. Since M abd N are the midpoints of AB and AC respectively,
¯¯¯m=¯a+¯b2and¯n=¯a+¯c2
∴¯¯¯¯¯¯¯¯MN=¯n−¯¯¯m
=(¯a+¯c2)−(¯a+¯b2)
=12(¯a+¯c−¯a−¯b)
=12(¯c−¯b)=12¯¯¯¯¯¯BC
Thus ¯¯¯¯¯¯¯¯MN is non-zero scalar multiple of ¯¯¯¯¯¯BC.
∴¯¯¯¯¯¯¯¯MN is parallel to ¯¯¯¯¯¯BC.
∴ seg MN is parallel to sed BC.
Also, ∣∣¯¯¯¯¯¯¯¯MN∣∣ ∴l(MN)=12⋅l(BC).

Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Theory Questions4videos
VECTORS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Examples for Practics28videos
VECTORS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Choice Questions12videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
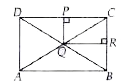
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
The line joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionProve that the line joining the middle points of the two sides of a triangle is parallel to the third side.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionProve that the line segment joining the middle points of two sides of a triangle is half the third side.
View SolutionThe line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
View Solutionprove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionThe line joining the midpoints of any two sides of a triangle is parallel to 3rd side and equal to half of it
View Solution

