Consider a gold nucleus to be a sphere of redius 6.9 fermi in whichprotons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separaton. Why do thes protons not fly apart under this repulsion
The largest separation between two Protons be =2r=fermi
So,F=9×109×(1.6×10−19)2(2r)2=1.2N.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Consider a sphere of radius R with charge density distributed as ρ(R)=kr for r≤Rand=0 for r>R.
(a) Find the electric field at all points r.
(b) suppose the total charge on the sphere is 2e, where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.
View SolutionThe nucleus in an iron atom has a radius of about 4.0×10−15m and contains 26 protons.
What is the magnitude of the repulsive electrostatic force between two of the protons that are separated by 4.0×10−15m?
View Solution
Knowledge Check
Repulsive force exist between two protons out side the nucleus. This is due to
AGravitational forceBElectromagnetic forceCWeak nuclear forceDStrong nuclear forceFind the electric force between two protons separated by a distance of 1 fermi (1fermi=1015m). The protons in a nucleus remain at a separation of this order.
A230NB2300NC23000NDNone of the Above
Two identical metallic sphere's having unequal opposite charges are placed at a distance 0.9 m apart in air. After bringing them in contact with each other they are again placed at the same distance apart. Now the force of repulsion between them is 0.025 N. calculate the final charges on each of them.
View SolutionTwo strange particles A and B in space, exert no force on each other when they are at a separation greater than x0=1.0 m. When they are at a distance less than x0, they repel one another along the line joining them. The repulsion force is constant and does not depend on the distance between the particles. This repulsive force produces an acceleration of 6ms–2 in A and 2ms–2 in B when the particles are at separation less than x0. In one experiment particle B is projected towards A with a velocity of 2ms–1 from a large distance so as to hit A head on. The particle A is originally at rest and the system of two particles do not experience any external force.
(a) Find the ratio of mass of A to that of B.
(b) Find the minimum distance between the particles during subsequent motion. (c) Find the final velocity of the two particles.
View SolutionAssertion: Forces acting between proton-proton (fpp), proton -neutron (fpn) and neutron -neutron (fnn) are such that fpp<fpn=fnn.
Reason: Electrostatic force of repulsion between two proton reduces net nuclear forces between them.
View SolutionSuppose ana attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2, (a) Write down the dimensional formulae and appporpriate SI units of C and k. (b) Suppose that k=1fermi−1 and that the repulsive electreic force between the protons is just blanced by the attractive nuclear force when the separation is 5 fermi. Find the value of c.
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?
View SolutionIn 1654 Otto von Guericke, inventor of the air pump, gave a demonstration before the noble-men of the Holy Roman Empire in which two teams of eight horses could not pull apart two evacuated brass hemispheres. (a) Assuming the hemispheres have (strong) thin walls, so that R in Fig. 14-63 may be considered both the inside and outside radius, show that the force →F required to pull apart the hemispheres has magnitude F=πR2Δp, where Δp is the difference between the pressures outside and inside the sphere,
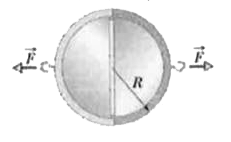
(b) Taking R as 40 cm, the inside pressure as 0.10 atm, and the outside pressure as 1.00 atm, find the force magnitude the teams of horses would have had to exert to pull apart the hemispheres. (c) Explain why one team of horses could have proved the point just as well if the hemispheres were attached to a sturdy wall.
View Solution
