The variation of radial probability density (r) as a function of distance r of the electron from the nucleus for 3p orbital:Solution in Telugu
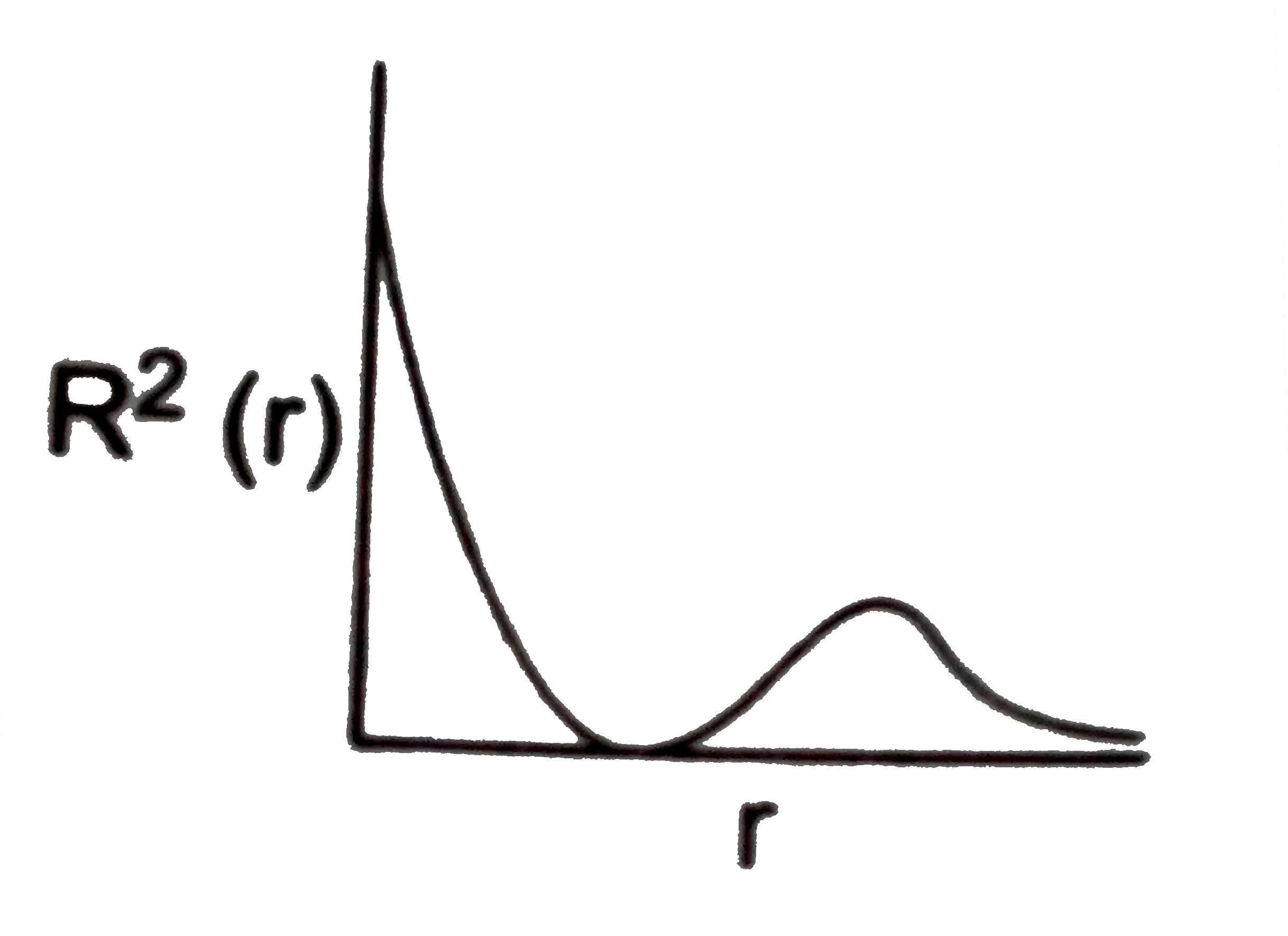
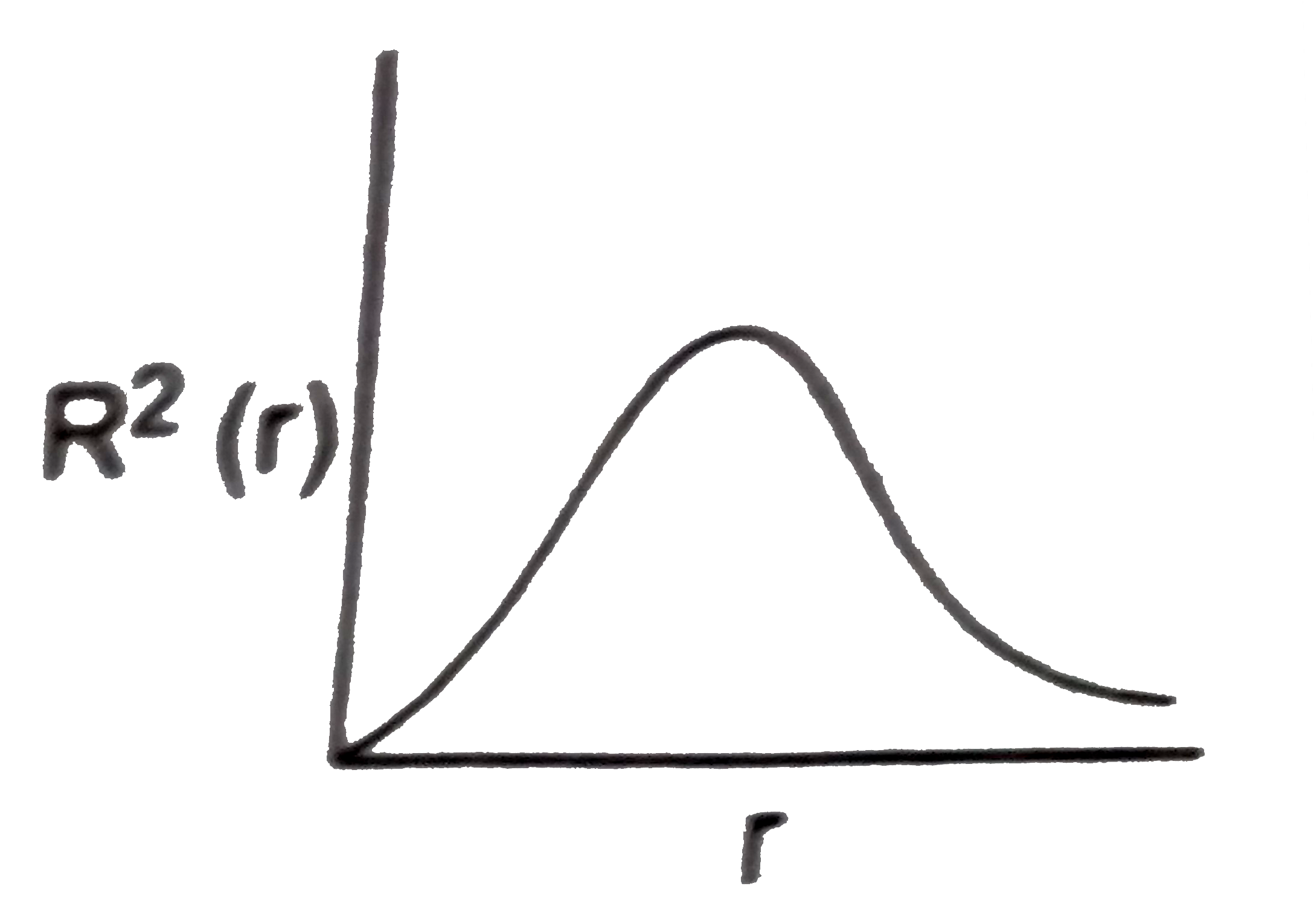
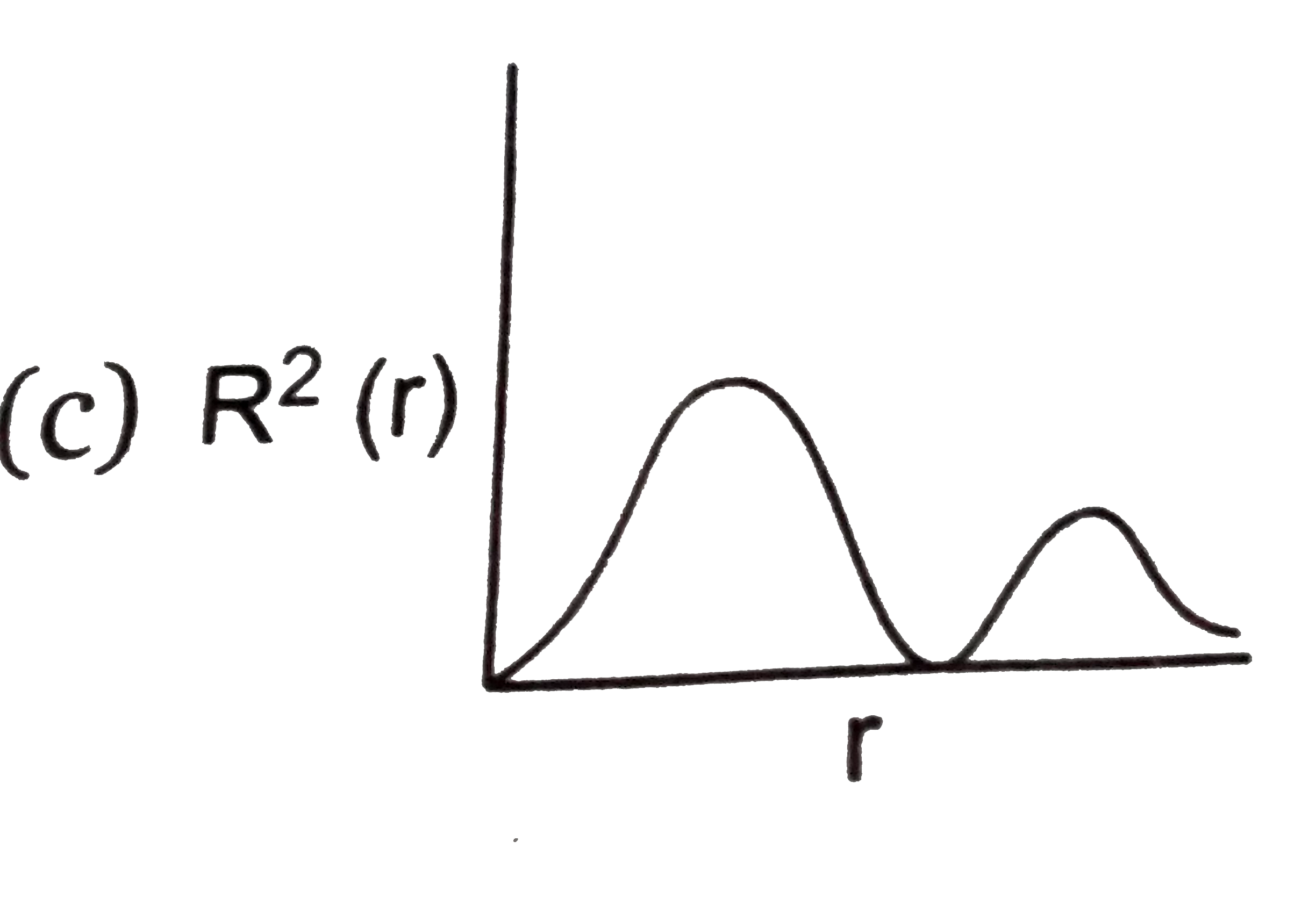
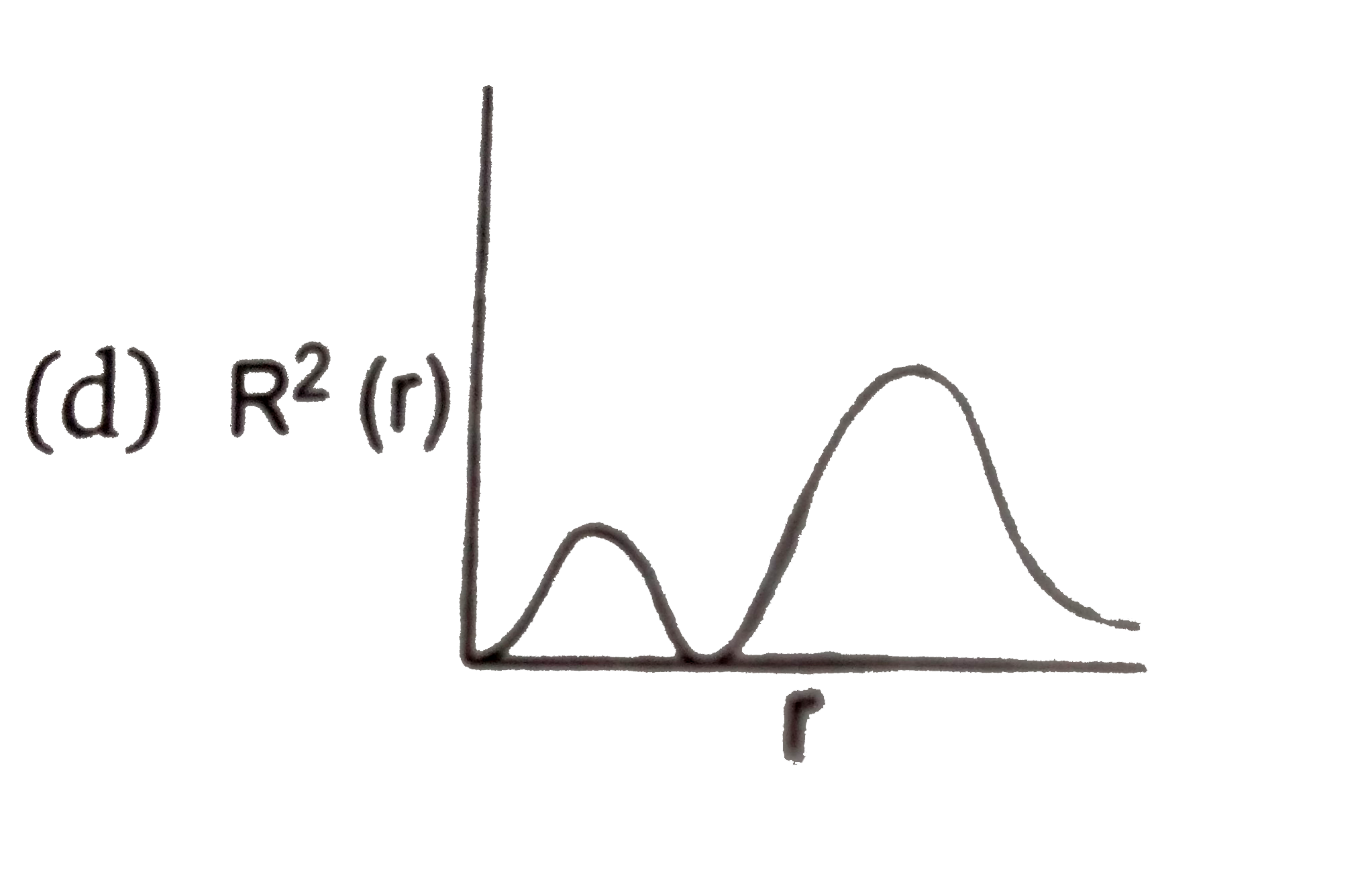
Step by step video & image solution for The variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
For similar orbitals having different values of n:
View SolutionA small particle of mass m moves in such a way that the potential energy U = ar2 where a is a constant and r is the distance of the particle from the origin. Assuming Bohr's model of quantization of angular momentum and circular orbits, find the radius of nth allowed orbit.
View SolutionCalculate ΔrG for the reaction at 27∘C
H2(g)+2Ag+(aq)⇔2Ag(s)+2H+(aq)
Given : PH2=0.5 bar, [Ag+]=10−5M,
[H+]=10−3M,ΔrG∘[Ag+(aq)]=77.1kJ/mol
View SolutionOPERATOR FORM SCHRODINGER WAVE EQUATION,PLOT OF RADIAL WAVE FUNCTION 'R',PLOT OF RADIAL PROBABILITY DENSITY 'R^2
View SolutionFor which of the following orbitals is the radial probaility density R^(2) the maximum at the nucleus and descrease sharply as the distance form the nucleus increases?
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View SolutionR(r) is the radial part of the wave function and r is the distance of electron from the nucleus.
View SolutionWhich of the following is correct graph between Probability density sπ2(r) vs radial distance of electron (r) form nucleus for 3 s ?
View SolutionAssertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical Reason. Probability density is Psi^(2) whereas radial probability function represents probability of finding the electron in a shell of thickness dr .
View SolutionThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r )=J_(0)(1-(r )/(R )) . The total current in the radial regon r = 0 to r=(R )/(4) will be :
View SolutionIf P(r) is the radial probability density for a hydrogen atom then the probability that the separation of the electron and proton is between r and r+ dr is
View SolutionThe variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: (A)(a) (b) (b) (c) (d)
View SolutionFor 1s orbital Hydrogen atom radial wave function is given as: R(r) =1/(sqrtpi) ((1)/(a_0))^(3//2) e^(-r//a_0) (where a_0 = 0.529 A^@ ) .The ratio of radial probability density of finding electron at r = a_0 to the radial probability density of finding electron at the nucleus is given as (x.e^(-y)) . Calculate the value of (x + y).
View SolutionThe radial probability is the probability of finding electron in a small spherical shell around the nucleus at a particular distance r. Hence radial probability is
View SolutionRepresent graphically, the variation of probability density (ψ2_(r)) as a function of distance (r ) of the electron from the nucleus for 1s and 2s orbitals.
View SolutionThe variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View Solution
