A 14.0 m cord of negligible mass is stretched horizontally between two supports. When a rock climber of weight 900 N hangs from the cord's midpoint, that midpoint sags by 0.85 m. What then is the tension in the cord?
To find the tension in the cord when a rock climber hangs from its midpoint, we can follow these steps:
Step 1: Understand the Setup
The cord is stretched horizontally between two supports, and when the climber hangs from the midpoint, the cord sags. The weight of the climber creates a downward force of 900 N at the midpoint.
Step 2: Analyze the Forces
At the midpoint where the climber hangs, the tension in the cord creates two components: a vertical component that balances the weight of the climber and a horizontal component that remains constant along the length of the cord.
Step 3: Determine the Geometry
When the cord sags, we can visualize a right triangle formed by:
- The vertical leg (sag) = 0.85 m
- The horizontal leg (half the length of the cord) = 7.0 m (since the total length of the cord is 14.0 m)
Step 4: Use Trigonometry
In the right triangle:
- The angle θ can be found using the sine function:
sin(θ)=saghypotenuse=0.85√(7.0)2+(0.85)2
However, we can also relate the tension directly to the weight and the sag without calculating θ explicitly.
Step 5: Set Up the Equation
Using the equilibrium of forces in the vertical direction:
2Tsin(θ)=900 N
Where T is the tension in the cord.
Step 6: Find sin(θ)
From the geometry of the triangle:
sin(θ)=saghypotenuse=0.85√(7.0)2+(0.85)2=0.85√49+0.7225=0.85√49.7225≈0.857.06≈0.120
Step 7: Substitute sin(θ) into the Equation
Now substituting sin(θ) into the equilibrium equation:
2T⋅0.120=900
Step 8: Solve for Tension T
T=9002⋅0.120=9000.240=3750 N
Final Answer
The tension in the cord is approximately 3750 N.
---
The cord is stretched horizontally between two supports, and when the climber hangs from the midpoint, the cord sags. The weight of the climber creates a downward force of 900 N at the midpoint.
At the midpoint where the climber hangs, the tension in the cord creates two components: a vertical component that balances the weight of the climber and a horizontal component that remains constant along the length of the cord.
When the cord sags, we can visualize a right triangle formed by:
- The vertical leg (sag) = 0.85 m
- The horizontal leg (half the length of the cord) = 7.0 m (since the total length of the cord is 14.0 m)
In the right triangle:
- The angle θ can be found using the sine function:
sin(θ)=saghypotenuse=0.85√(7.0)2+(0.85)2
Using the equilibrium of forces in the vertical direction:
2Tsin(θ)=900 N
Where T is the tension in the cord.
From the geometry of the triangle:
sin(θ)=saghypotenuse=0.85√(7.0)2+(0.85)2=0.85√49+0.7225=0.85√49.7225≈0.857.06≈0.120
Now substituting sin(θ) into the equilibrium equation:
2T⋅0.120=900
T=9002⋅0.120=9000.240=3750 N
The tension in the cord is approximately 3750 N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS28videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
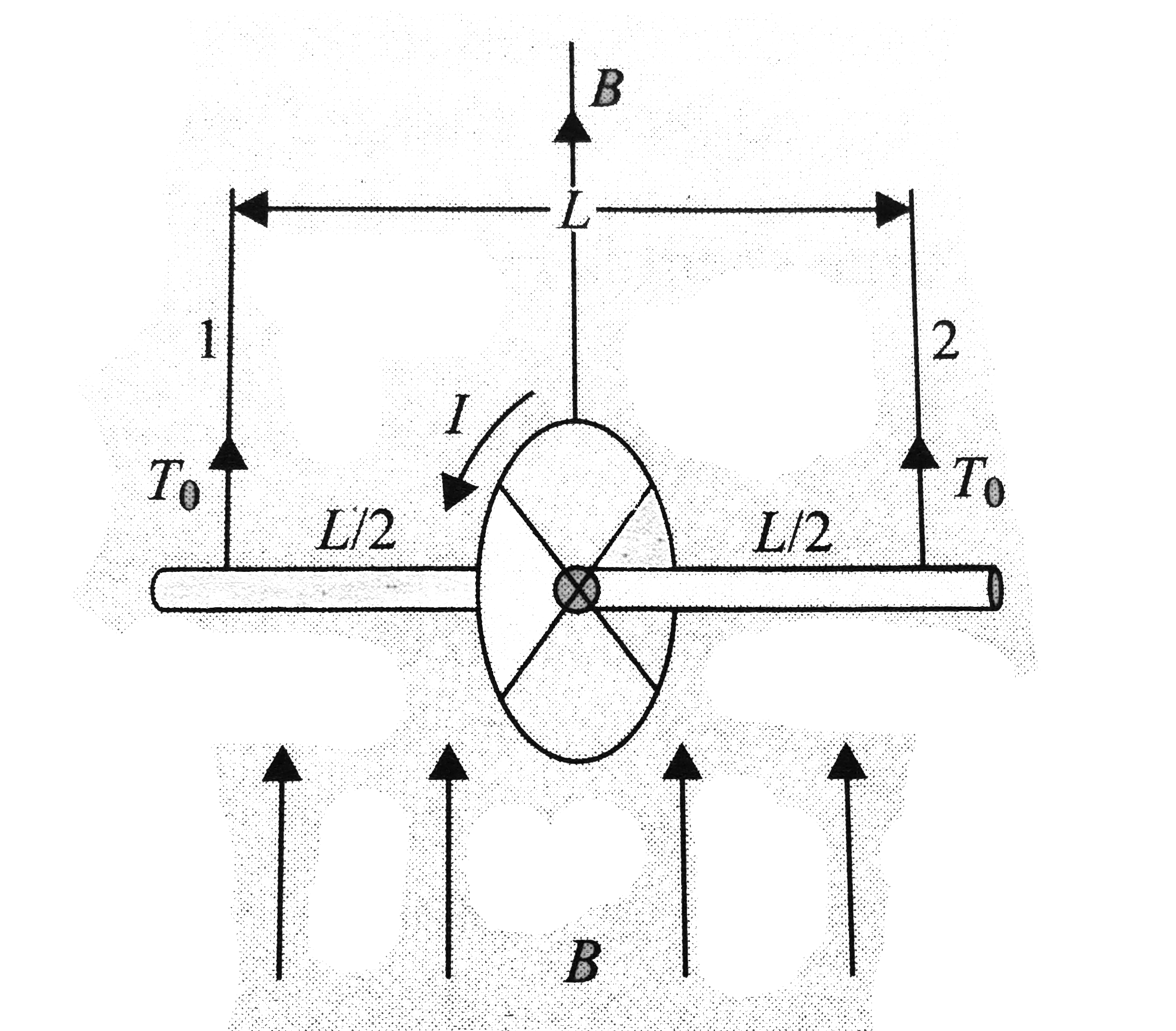
The circular current loop of radius b shown in Fig. is mounted rigidly on the axle, midway between the two supporting cords. In the absence of an external magnetic field, the tensions in the cords are equal and are T0.
a. What will be the tensions in the two cords when the vertical magnetic field B is present?
b. Repeat if the field is parallel to the axis.
 View Solution
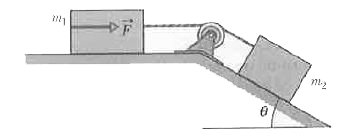
View SolutionFigure 5-59 shows a box of mass m2=1.0 kg on a friction-less plane inclined at angle θ=30∘. It is connected by a cord of negligible mass to a mass m1=2.5 kg on a horizontal frictionless surface. The pulley is frictionless and massless. (a) If the magnitude of horizontal force →F is 2.3 N, what is the tension in the connecting cord? (b) What is the largest value the magnitude of →F may have without the cord becoming slack?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cord of negligible mass is wound round the rin of a flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. The work done by the pull when 2 m of the cord is unwound is
A20 JB25 JC45 JD50 J - Question 2 - Select One
The figure shows a uniform disc, with mass M = 2.4 kg and radius R= 20 cm, mounted on a fixed horizontal axle. A block of mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disc. The tension in the cord is
 A12 NB20 NC24 NDnone of these
A12 NB20 NC24 NDnone of these - Question 3 - Select One
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
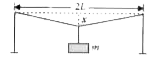
A mass m is suspended from the midpoint of the wire. Strain in the wire isAx22L2BxLCx2LDx22L
A cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
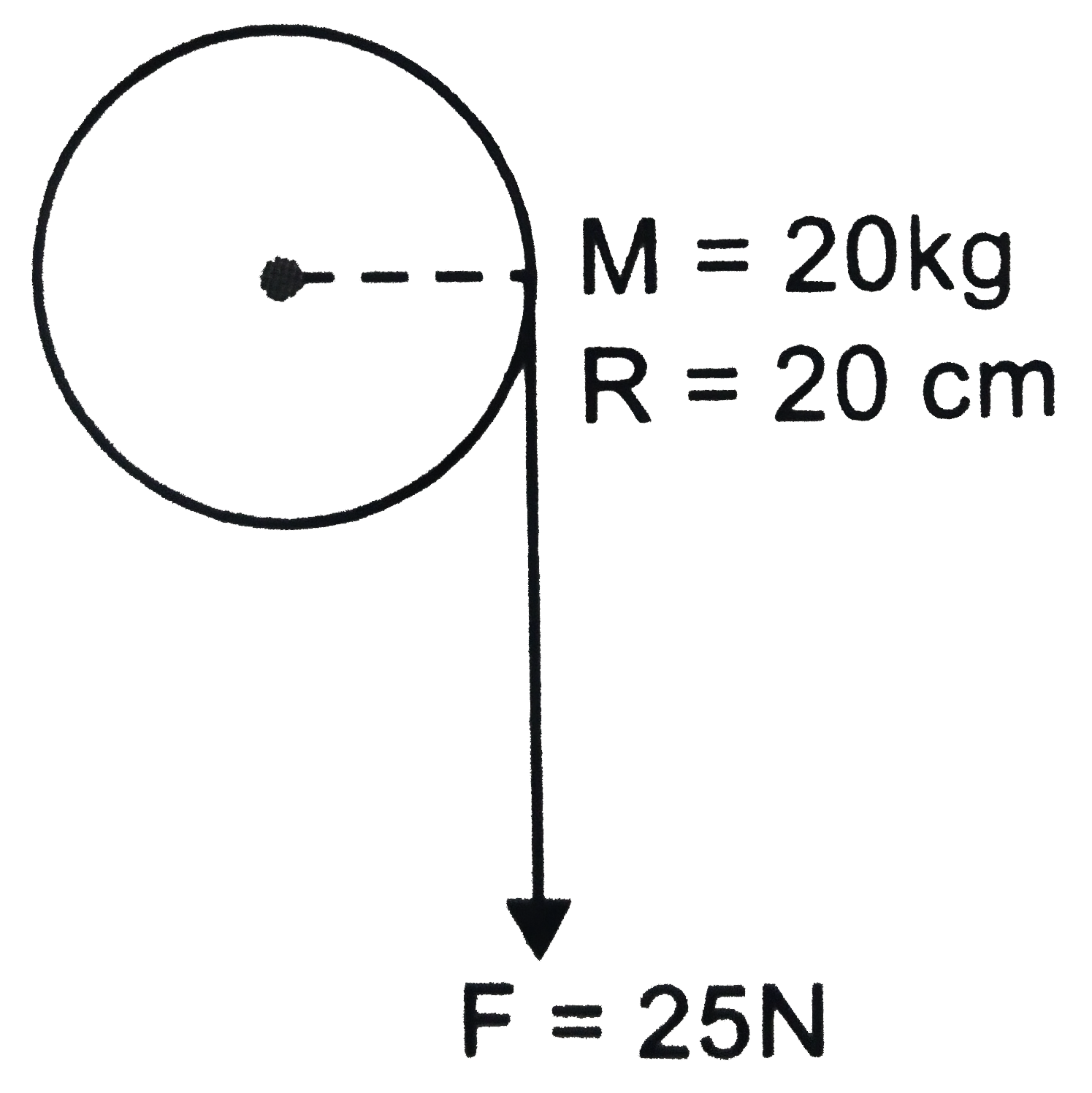
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).View SolutionA cord with negligible mass is wrapped around a pulley that is a uniform disk of mass 5.00 kg and radius 0.300 m and that can rotate without friction about its central axis. A 1.0 kg bucket is attached at the free end of the cord hanging down from the pulley and then released at time t = 0. The cord begins to unwrap from the pulley as the bucket descends. At t = 5.00 s, through how many rotations has the pulley turned (the bucket is still descending)?
View SolutionAB is a vertically suspended elastic cord of negligible mass and length L. Its force constant is k=4mgL. There is a massless platform attached to the lower end of the cord. A monkey of mass m starts from top end A and slides down the cord with a uniform acceleration of g2 . Just before landing on the platform, the monkey loses grip on the cord. After landing on the platform the monkey stays on it. Calculate the maximum extension in the elastic cord.
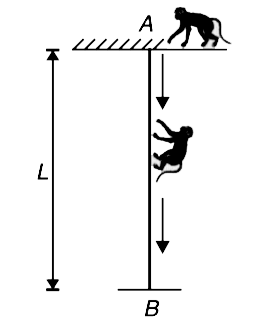 View Solution
View SolutionA block of mass m1=3.70 kg on a frictionless plane inclined at angle 30.0∘ is connected by a cord over a massless, frictionless pulley to a second block of mass m2=2.30 kg (see Fig. 5-32).
(a) What is the magnitude of the acceleration of each block?
(b) What is the direction of the acceleration of the hanging block ?
(c) What is the tension in the cord? View Solution
View SolutionA cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
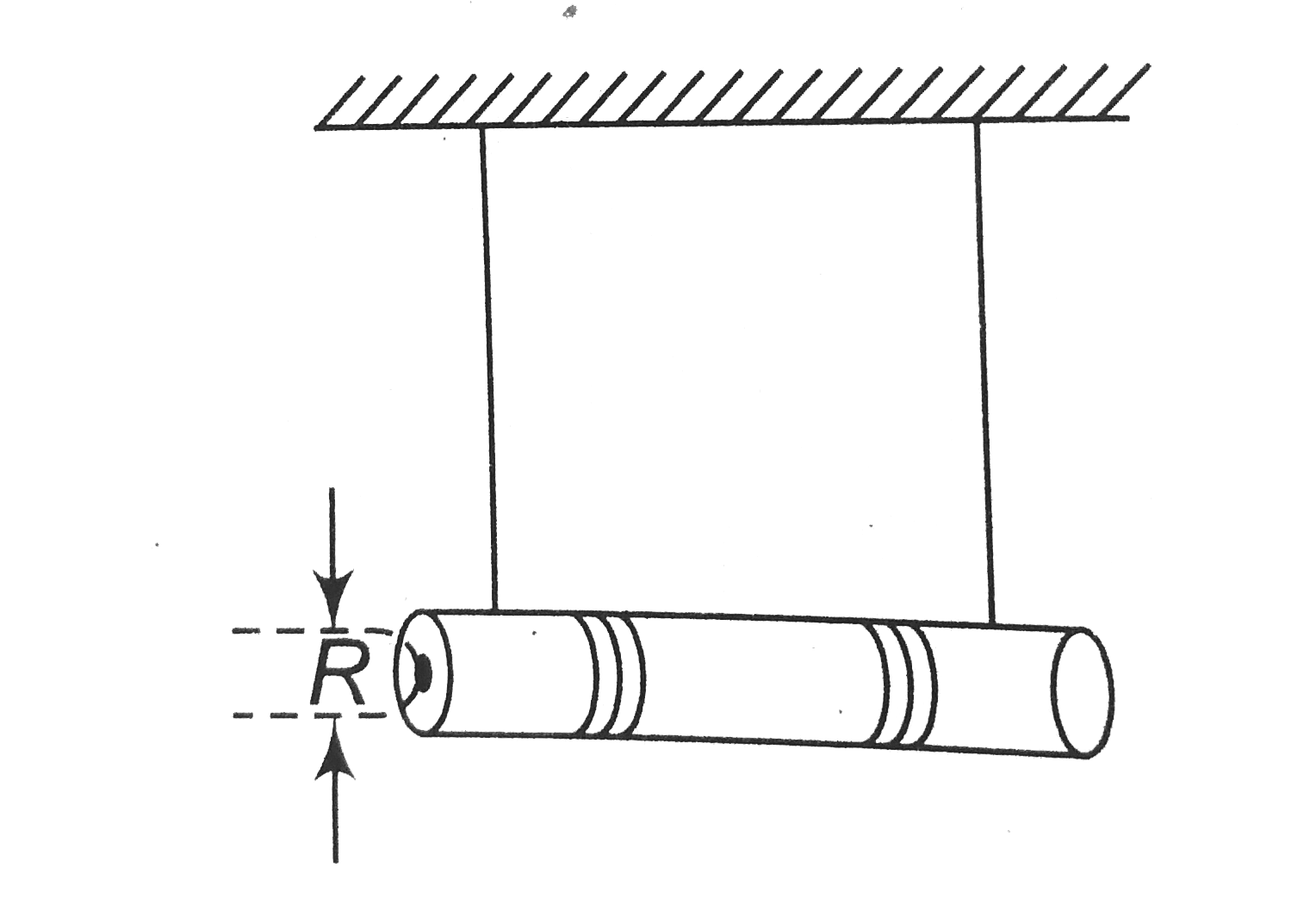 .View Solution
.View Solution

