Question

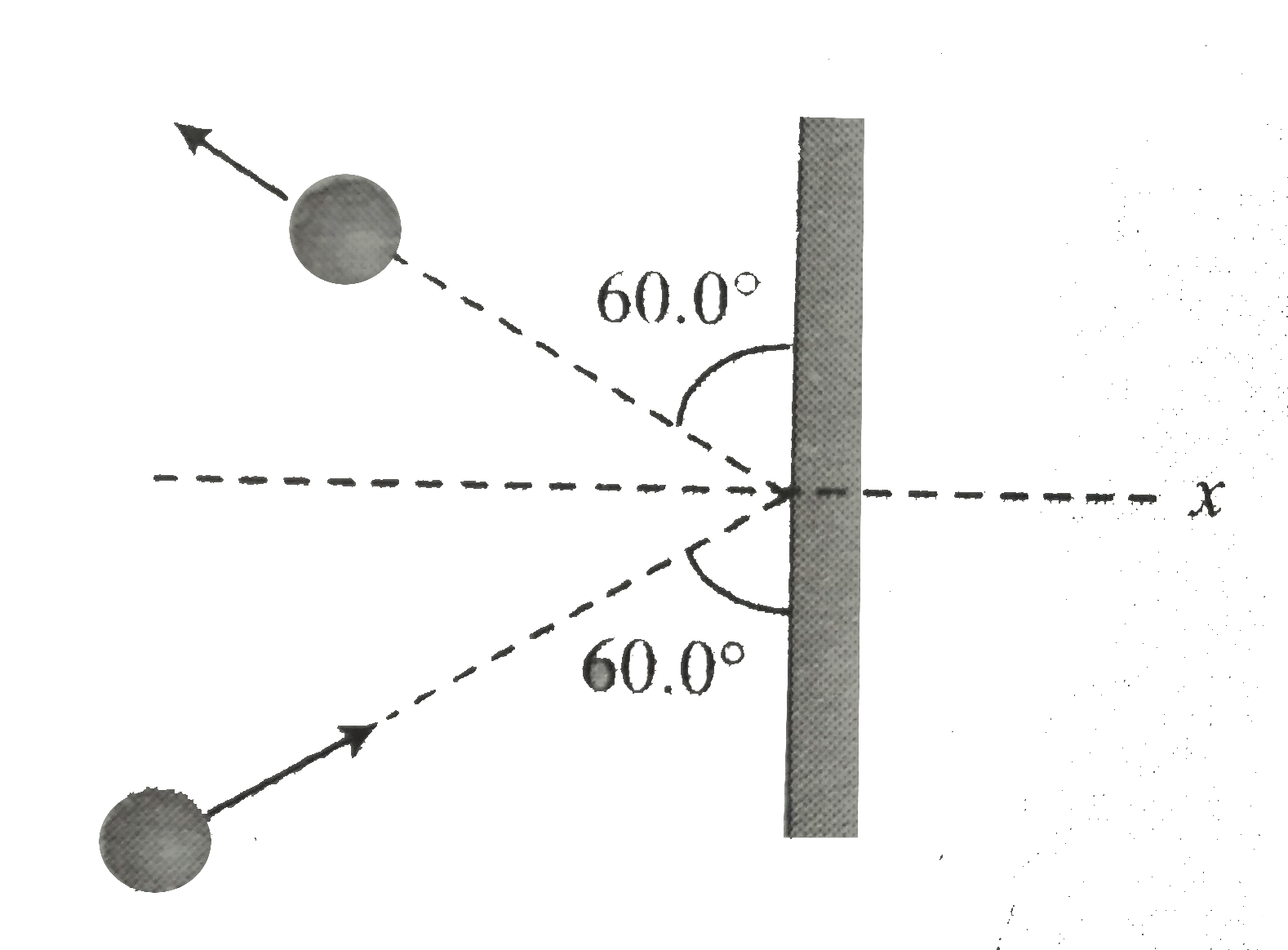
A $3.00kg$ steel hall strikes the wall with a speed of $10.0m/s$ at an angle of ${60}^{\circ }$ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for $0.200s$, what is the average force exerted by the wall on the ball?

Explanation

To solve the problem, we will follow these steps:

Step 1: Identify the components of velocity
The ball strikes the wall at an angle of \(60^\circ\) with the surface at a speed of \(10.0 \, \text{m/s}\). We need to resolve this velocity into two components:
- Perpendicular to the wall: \(V_{\perp} = V \sin(60^\circ)\)
- Parallel to the wall: \(V_{\parallel} = V \cos(60^\circ)\)

Step 2: Calculate the components
Using \(V = 10.0 \, \text{m/s}\):
- \(V_{\perp} = 10.0 \sin(60^\circ) = 10.0 \times \frac{\sqrt{3}}{2} = 5\sqrt{3} \, \text{m/s}\)
- \(V_{\parallel} = 10.0 \cos(60^\circ) = 10.0 \times \frac{1}{2} = 5.0 \, \text{m/s}\)

Step 3: Determine the change in momentum
The momentum before and after the collision can be analyzed:
- Initial momentum perpendicular to the wall: \(p_{\text{initial}} = m V_{\perp} = 3.00 \, \text{kg} \times 5\sqrt{3} \, \text{m/s}\)
- Final momentum perpendicular to the wall: Since the ball bounces back, the final momentum is \(p_{\text{final}} = -m V_{\perp} = -3.00 \, \text{kg} \times 5\sqrt{3} \, \text{m/s}\)

The change in momentum (\(\Delta p\)) is given by:
\( \Delta p = p_{\text{final}} - p_{\text{initial}} = -3.00 \times 5\sqrt{3} - (3.00 \times 5\sqrt{3}) = -6.00 \times 5\sqrt{3} \)
This results in:
\( \Delta p = -6.00 \times 5\sqrt{3} = -30\sqrt{3} \, \text{kg m/s} \)

Step 4: Calculate the average force
The average force exerted by the wall on the ball can be calculated using the formula:
\( F_{\text{avg}} = \frac{\Delta p}{\Delta t} \)
Given that \(\Delta t = 0.200 \, \text{s}\):
\( F_{\text{avg}} = \frac{-30\sqrt{3}}{0.200} \)
Calculating this gives:
\( F_{\text{avg}} = -150\sqrt{3} \, \text{N} \)
The negative sign indicates the direction of the force is opposite to the initial momentum direction. The magnitude of the force is:
\( F_{\text{avg}} \approx 150 \times 1.732 = 259.8 \, \text{N} \)

Final Answer
The average force exerted by the wall on the ball is approximately \(259.8 \, \text{N}\).

---