a. A 2−kg situated on a smooth fixed incline is connected to a spring of negligible mass, with spring constant k=100Nm−1, via a frictionless pulley. The block is released from rest when the spring is unstretched. How far does the block moves down the incline before coming (momentarily) to rest? What is its acceleration at its lower point?
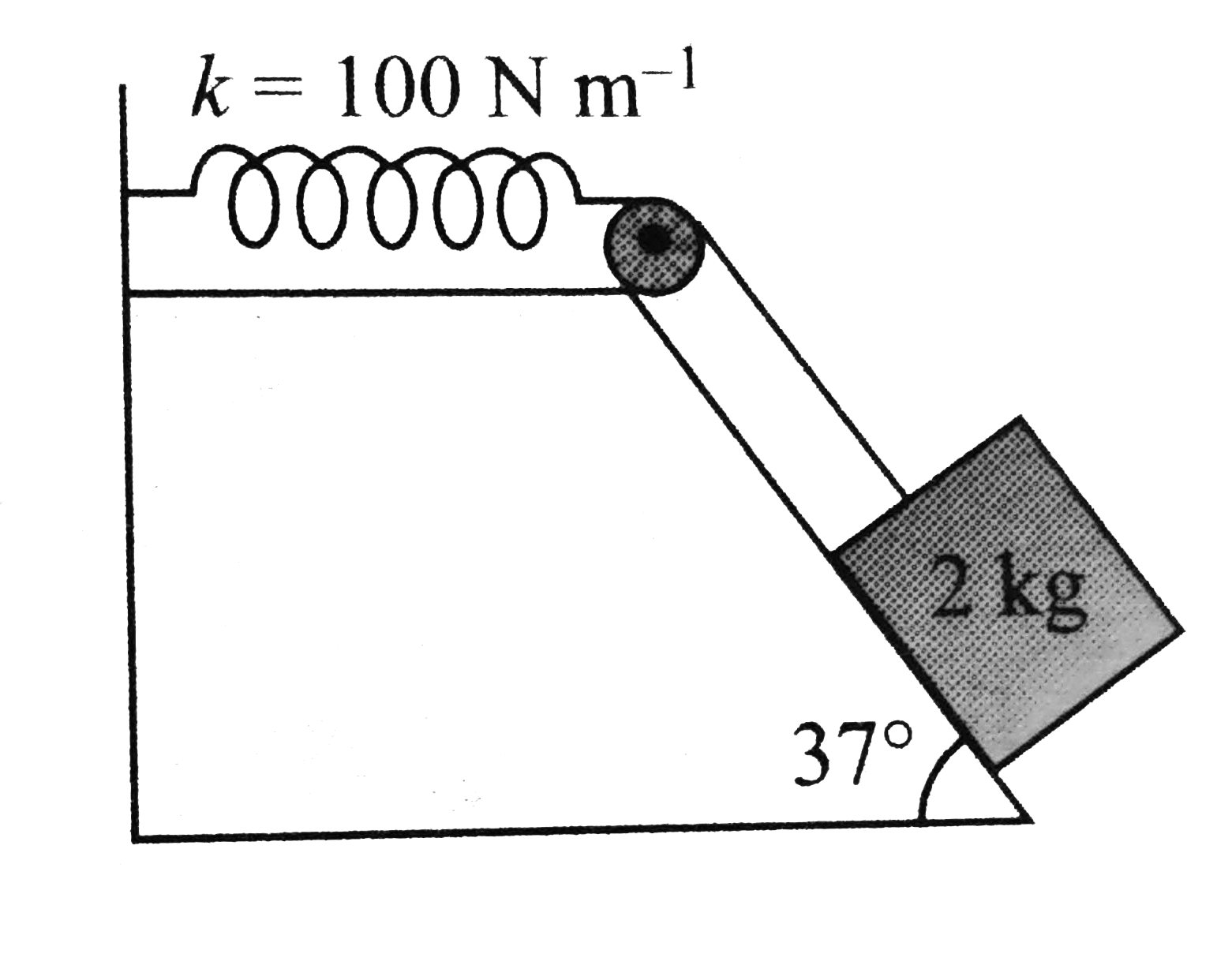
b. The experiment is repeated on a rough incline. If the block is observed to move 0.20m down along the incline before it comes to instantaneous rest, calculate the coefficient of kinetic friction.
The correct Answer is:a. 24m; 6ms−2, b. 18
(a) At the extreme position blocks stops.
Applying work-energy theorem, we get
mgsin37∘=12ks2
2×10×s×35=12×100×s2
On solving s=0.24m
Acceleration at its lowest point, a=ks−mgsin37∘m
=100×0.24−2×10×352=6ms−2
(b) Wg+Wfriction+Wspring=ΔKE
mgsin37∘+μmgcos37∘×s=12ks2
mgsin37∘−12ks=μmgcos37∘
2×10×35−12×100×s=μ×2×10×45
Gives s=0.020m
μ=12−50s16⇒μ=18
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution
Knowledge Check
A 1 kg block situated on a rough incline is connected to a spring of negligible mass having spring constant 100Nm−1 as shown in the figure.The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. The coefficient of friction between the block and the incline is (Take g=10ms−2 and assume that the pulley is frictionless)
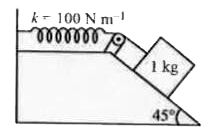 A0.2B0.3C0.5D0.6
A0.2B0.3C0.5D0.6A 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
 AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwardsFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mg
In the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
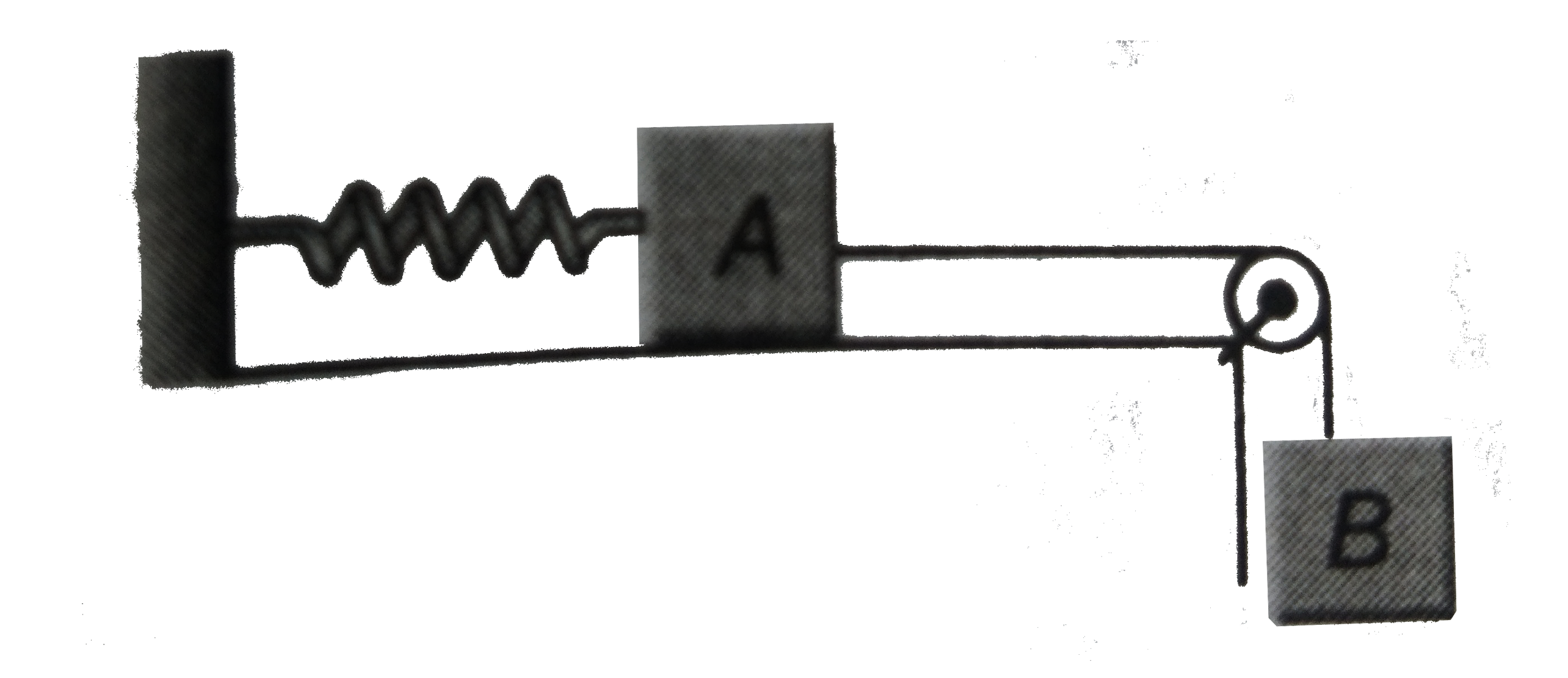 .
.
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
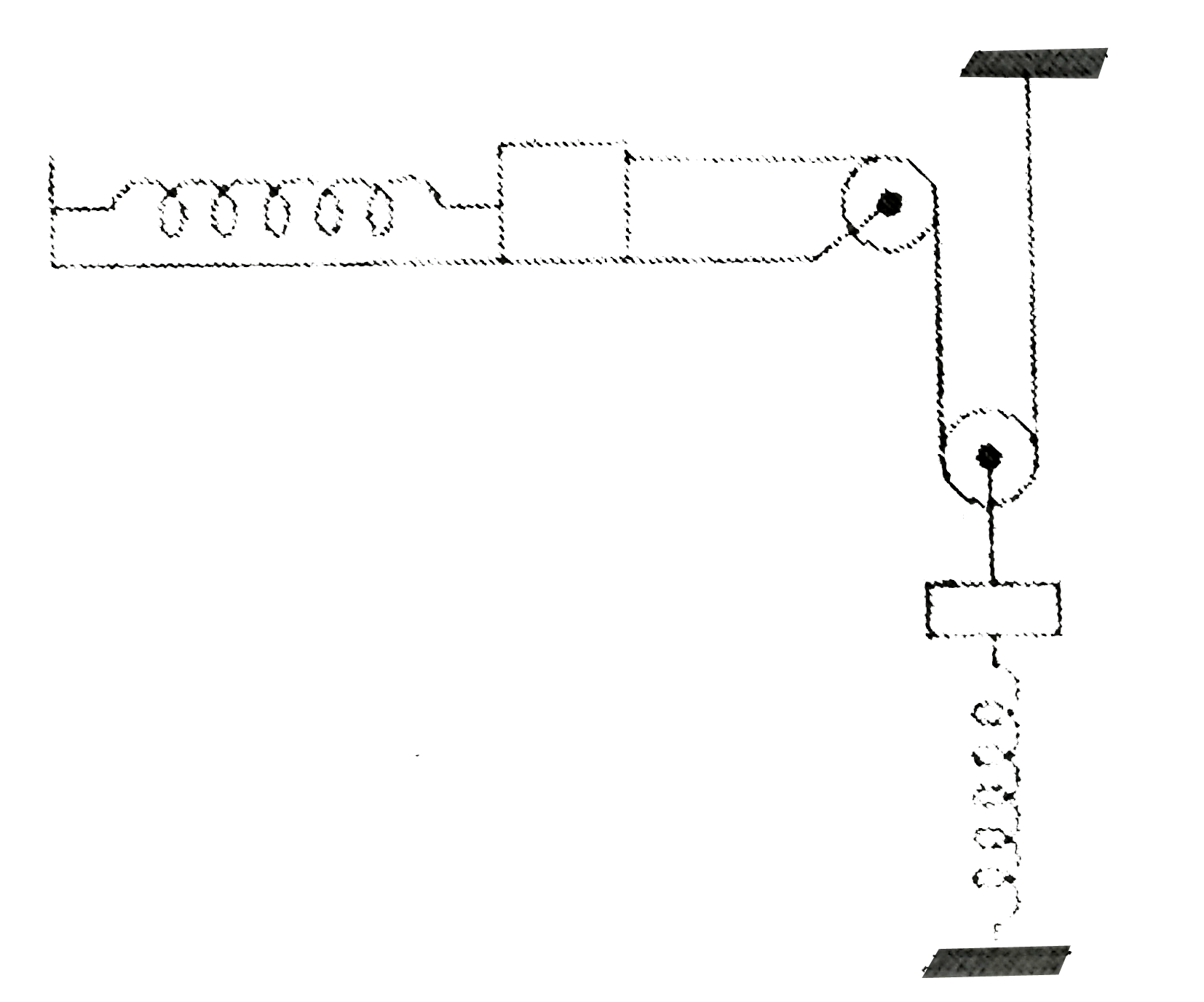
In the equilibrium position, speed of the block placed horizontally is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m. Extension of horizontal spring in equilibrium is:

View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
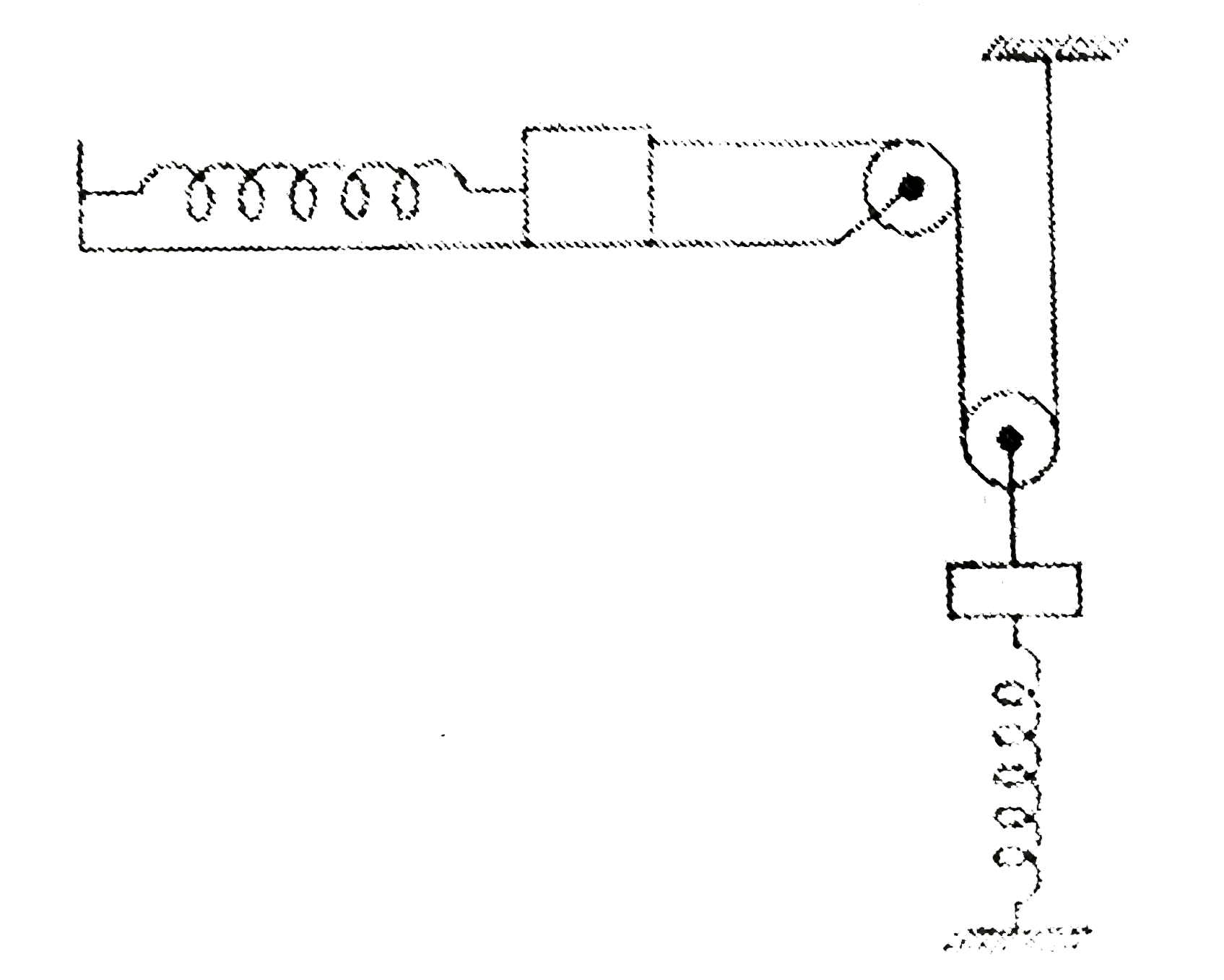
Extension of horizontal spring in equilibrium is
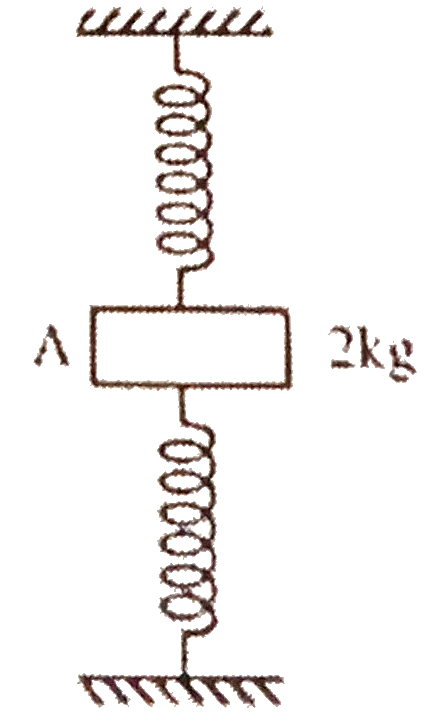
View SolutionA block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
View Solution