A ball collides with an inclined plane of inclination θ after falling through a distance h. if it moves horizontal just after the impact, the coefficient of restitution is
tan2θ
cot2θ
tanθ
cotθ
To solve the problem, we need to find the coefficient of restitution (e) when a ball collides with an inclined plane after falling through a distance h and moves horizontally just after the impact. Let's break down the solution step by step.
1. Understanding the Problem:
- A ball falls a distance h and collides with an inclined plane at an angle θ.
- After the collision, the ball moves horizontally.
2. Velocity Before Impact:
- The velocity of the ball just before impact can be calculated using the equation of motion for free fall:
v0=√2gh
where g is the acceleration due to gravity.
3. Components of Velocity:
- When the ball strikes the inclined plane, its velocity can be resolved into two components:
- Perpendicular to the inclined plane: v0cosθ
- Parallel to the inclined plane: v0sinθ
4. Velocity After Impact:
- After the impact, the ball moves horizontally, meaning its velocity in the direction perpendicular to the inclined plane is 0.
- The velocity of the ball after impact can be denoted as v.
5. Applying the Coefficient of Restitution:
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- In this case:
- Velocity of separation (after impact): v
- Velocity of approach (before impact): v0cosθ
6. Setting Up the Equation:
- Since the inclined plane is not moving, the velocity of approach can be simplified to:
e=vv0cosθ
7. Conservation of Momentum Along the Inclined Plane:
- The component of velocity along the inclined plane remains unchanged during the collision:
v0sinθ=vcosθ
- Rearranging gives:
vv0=tanθ
8. Substituting Back:
- Substitute vv0=tanθ into the equation for e:
e=vv0cosθ=tanθcosθ=sinθcos2θ
9. Final Result:
- Thus, the coefficient of restitution is:
e=tan2θ
Conclusion:
The coefficient of restitution e is given by:
e=tan2θ
- A ball falls a distance h and collides with an inclined plane at an angle θ.
- After the collision, the ball moves horizontally.
- The velocity of the ball just before impact can be calculated using the equation of motion for free fall:
v0=√2gh
where g is the acceleration due to gravity.
- When the ball strikes the inclined plane, its velocity can be resolved into two components:
- Perpendicular to the inclined plane: v0cosθ
- Parallel to the inclined plane: v0sinθ
- After the impact, the ball moves horizontally, meaning its velocity in the direction perpendicular to the inclined plane is 0.
- The velocity of the ball after impact can be denoted as v.
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- In this case:
- Velocity of separation (after impact): v
- Velocity of approach (before impact): v0cosθ
- Since the inclined plane is not moving, the velocity of approach can be simplified to:
e=vv0cosθ
- The component of velocity along the inclined plane remains unchanged during the collision:
v0sinθ=vcosθ
- Rearranging gives:
vv0=tanθ
- Substitute vv0=tanθ into the equation for e:
e=vv0cosθ=tanθcosθ=sinθcos2θ
- Thus, the coefficient of restitution is:
e=tan2θ
The coefficient of restitution e is given by:
e=tan2θ
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Video
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A ball falls from height h over an inclined plane of inclination 30∘ as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_224_Q01.png)
View SolutionA ball falls from height h over an inclined plane of inclination 30°C as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_E05_227_Q001.png)
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friciton is μ)
View SolutionA block is kept on a inclined plane of inclination θ of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is μ
View SolutionA ball is dropped on a large smooth inclined plane of angle of inclination 37∘, from a height of 209m above the point of impact. The coefficient of restitution of the impact is e=916 then :
[Take g=10m/s2]
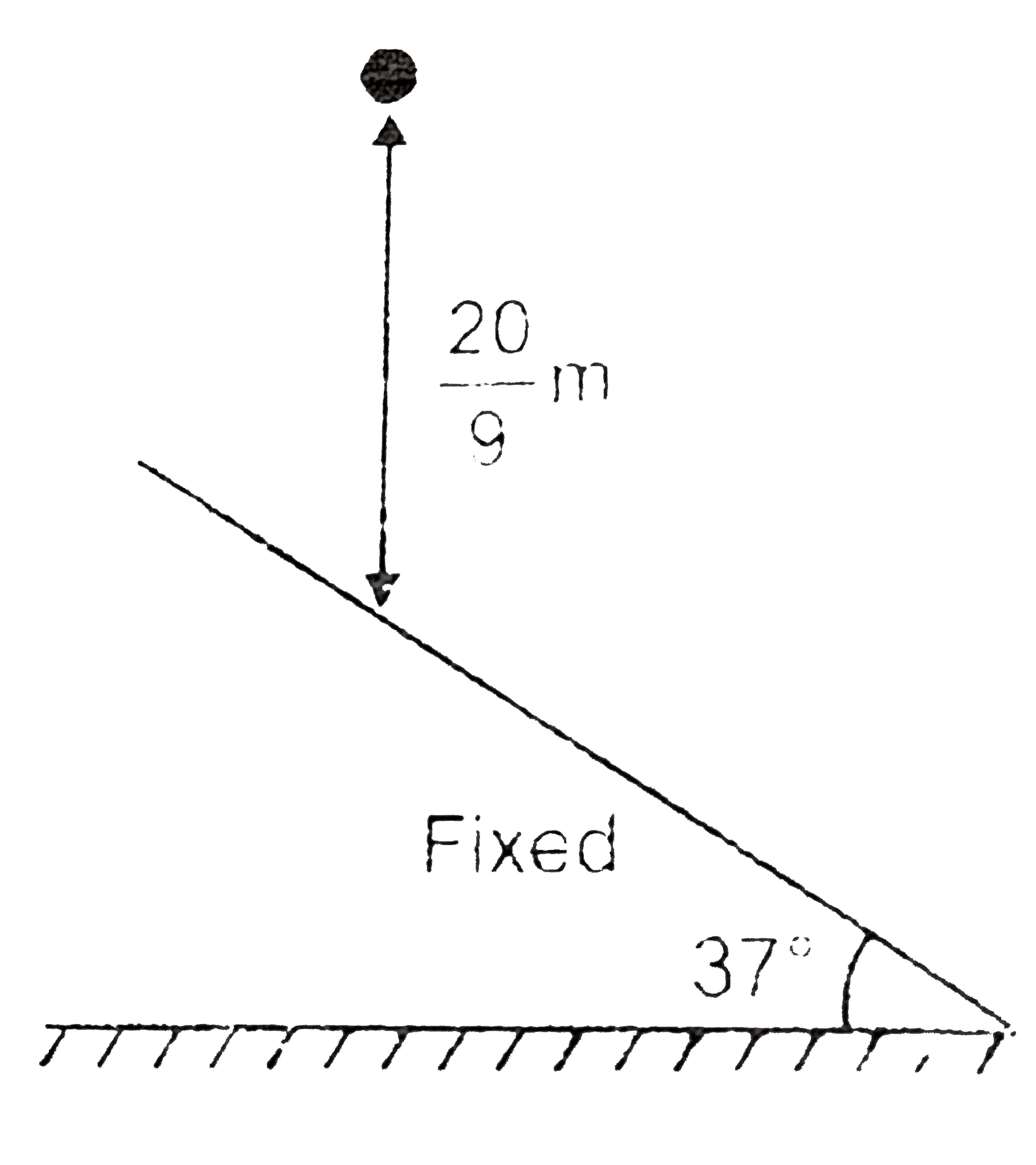
View SolutionA ball is dropped on a smooth inclined plane and is observed to move horizontally after the impact. The coefficient of restitution between the plane and ball is e. The inclination of the plane is
View SolutionWhen a body of mass M slides down an inclined plane of inclination θ, having coefficient of friction μ through a distance s, the work done against friction is :
View SolutionA ball of mass m strikes the fixed inclined plane after falling through a height h. if it rebounds elastically. The impulse on the ball is :
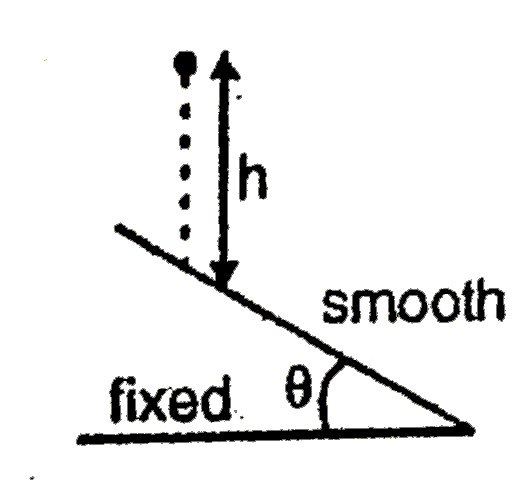
View SolutionTwo identical billiard balls are in contact on a table. A third identical ball strikes them symmetrically and comes to rest after impact. The coefficient of restitution is :
View SolutionA small mass slides down an inclined plane of inclination θ with the horizontal the coefficient of friction is μ=μ0x, where x is the distance through which the mass slides down. Then the distance covered by the mass before it stops is
View Solution