A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 450. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate a. the magnitude of the change in momentum of the ball b. the change in the magnitude of the momentum of the wall.
To solve the problem step by step, we will break it down into two parts: (a) calculating the magnitude of the change in momentum of the ball and (b) calculating the change in the magnitude of the momentum of the wall.
Step 1: Understand the problem
We have a ball of mass m=50g=0.05kg moving at a speed v=2.0m/s that strikes a plane surface at an angle of incidence 45∘. The ball is reflected at the same angle with the same speed.
Step 2: Resolve the initial momentum into components
The initial velocity of the ball can be resolved into two components:
- Horizontal component (x-direction):
vix=vcos(45∘)=2⋅1√2=2√2=√2m/s
- Vertical component (y-direction):
viy=vsin(45∘)=2⋅1√2=√2m/s
Step 3: Calculate initial momentum components
The initial momentum components of the ball are:
- Initial momentum in the x-direction:
pix=mvix=0.05⋅√2kg m/s
- Initial momentum in the y-direction:
piy=mviy=0.05⋅√2kg m/s
Step 4: Determine the final momentum components
After the collision, the ball reflects off the wall:
- The horizontal component (x-direction) will change direction:
vfx=−vix=−√2m/s
- The vertical component (y-direction) remains the same:
vfy=viy=√2m/s
The final momentum components are:
- Final momentum in the x-direction:
pfx=mvfx=0.05⋅(−√2)kg m/s
- Final momentum in the y-direction:
pfy=mvfy=0.05⋅√2kg m/s
Step 5: Calculate the change in momentum
The change in momentum components can be calculated as:
- Change in x-direction:
Δpx=pfx−pix=0.05⋅(−√2)−0.05⋅√2=−0.1⋅√2kg m/s
- Change in y-direction:
Δpy=pfy−piy=0.05⋅√2−0.05⋅√2=0kg m/s
Step 6: Calculate the magnitude of the change in momentum
The total change in momentum is:
Δp=√(Δpx)2+(Δpy)2=√(−0.1⋅√2)2+02=0.1⋅√2kg m/s
Calculating this gives:
Δp=0.1⋅1.414≈0.1414kg m/s
Step 7: Change in momentum of the wall
Since the wall is stationary and does not move, the change in momentum of the wall is equal to the negative of the change in momentum of the ball:
Δpwall=−Δpball=−0.1414kg m/s
Final Answers
(a) The magnitude of the change in momentum of the ball is approximately 0.1414kg m/s.
(b) The change in the magnitude of the momentum of the wall is −0.1414kg m/s.
We have a ball of mass m=50g=0.05kg moving at a speed v=2.0m/s that strikes a plane surface at an angle of incidence 45∘. The ball is reflected at the same angle with the same speed.
The initial velocity of the ball can be resolved into two components:
- Horizontal component (x-direction):
vix=vcos(45∘)=2⋅1√2=2√2=√2m/s
- Vertical component (y-direction):
viy=vsin(45∘)=2⋅1√2=√2m/s
The initial momentum components of the ball are:
- Initial momentum in the x-direction:
pix=mvix=0.05⋅√2kg m/s
- Initial momentum in the y-direction:
piy=mviy=0.05⋅√2kg m/s
After the collision, the ball reflects off the wall:
- The horizontal component (x-direction) will change direction:
vfx=−vix=−√2m/s
- The vertical component (y-direction) remains the same:
vfy=viy=√2m/s
- Final momentum in the x-direction:
pfx=mvfx=0.05⋅(−√2)kg m/s
- Final momentum in the y-direction:
pfy=mvfy=0.05⋅√2kg m/s
The change in momentum components can be calculated as:
- Change in x-direction:
Δpx=pfx−pix=0.05⋅(−√2)−0.05⋅√2=−0.1⋅√2kg m/s
- Change in y-direction:
Δpy=pfy−piy=0.05⋅√2−0.05⋅√2=0kg m/s
The total change in momentum is:
Δp=√(Δpx)2+(Δpy)2=√(−0.1⋅√2)2+02=0.1⋅√2kg m/s
Calculating this gives:
Δp=0.1⋅1.414≈0.1414kg m/s
Since the wall is stationary and does not move, the change in momentum of the wall is equal to the negative of the change in momentum of the ball:
Δpwall=−Δpball=−0.1414kg m/s
(a) The magnitude of the change in momentum of the ball is approximately 0.1414kg m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 450. The ball is reflected by the plane at an equal angle of reflection with the same speed. Calculate (a). the magnitude of the change in momentum of the ball (b). the change in the magnitude of the mometum of the ball.
View SolutionA mass m with velocity u strikes a wall normally and returns with same speed. What is the magnitude of the change in momentum of the body when it returns.
View SolutionA ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle calculate the change in momentum
View SolutionA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is

View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
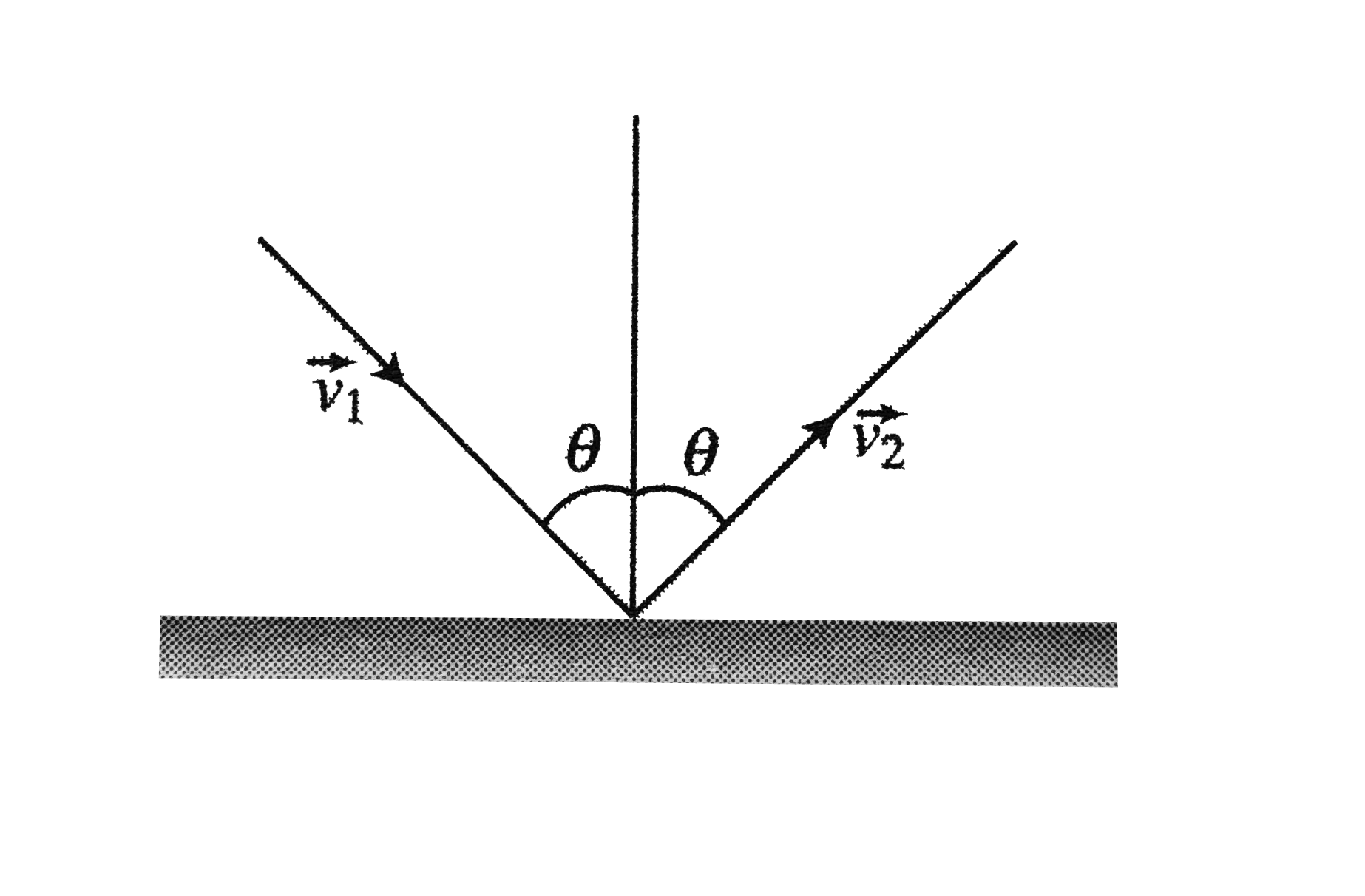
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.

View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionA ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View Solution
