
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its forward english (backward slipping) eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.
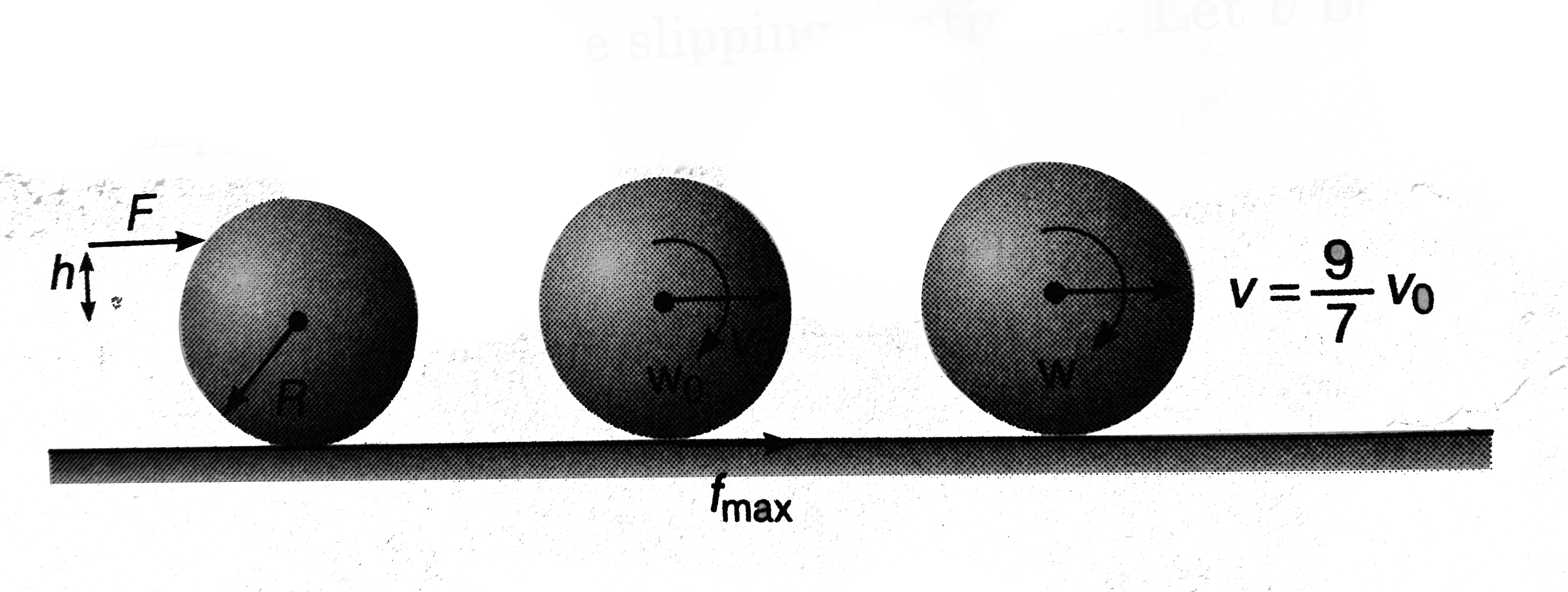
let ω0 be the angular speed of the ball just after it leaves the cue. The maximum friction acts in forward direction till the slipping continues. Let v be the linear speed and ω the angular speed when slipping is ceased.
∴v=Rω or ω=vR
given v=97v0 ...(i)
∴ω=97v0R ...(ii)
Applyingg linear impulse = change in angular momentum
∴Fdt=mv0 ..(iii)
Angular impulse = change in angular momentum
∴τdt=Iω0 or (Fh)dt=25mR2ω0 ..(iv)
During the slip angular momentum about bottommost point will remain conserved
i.e., Li=Lf
or Iω0+mRv0=Iω+mRv
∴25mR2ω0+mRv0=25mR2(97v0R)+97mRv0 ..(v)
solving eqs. (iii). (iv) and (v) we get h=45R
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The cue stick hits a cue ball horizontally a distance x above the centre of the ball. Find the value of x for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius R of the ball.

View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View Solution
Knowledge Check
A billiard ball of mass m and radius 7, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity Wo acquired by the ball is
A5v0r22hB2v0r25hC2v0h5r2D5v0h2r2A solid shperical ball of mass m and radius R is present on a rough horizontal surface. A person hit the ball at distance h above the centre of the ball as shown in the figure. Find out the h such that the ball starts pure rolling just after impact.
 Ah=R5Bh=3R5Ch=RDh=2R5
Ah=R5Bh=3R5Ch=RDh=2R5Five balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed v0 towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
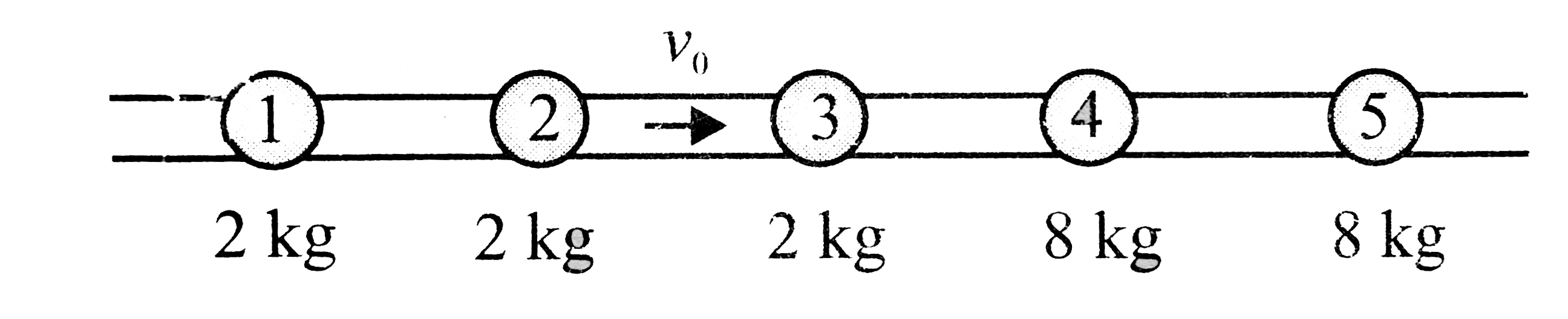 ATotal number of collisions in the process is 5BVelocity of separation between the first and fifth ball after the last possible collision is v0CFinally, three balls remain stationary.DAll of the above
ATotal number of collisions in the process is 5BVelocity of separation between the first and fifth ball after the last possible collision is v0CFinally, three balls remain stationary.DAll of the above
A billiard ball is struck by a cue. The line of action of the applied impulse is horizontal andpasses through thecentre of theball. The initial velocityofthe ball is v0. If is the radius, M is the mass of the ball and μ is the coefficient of friction between the ball and the floor, find how far the ball moves before it ceases to slip on the floor.
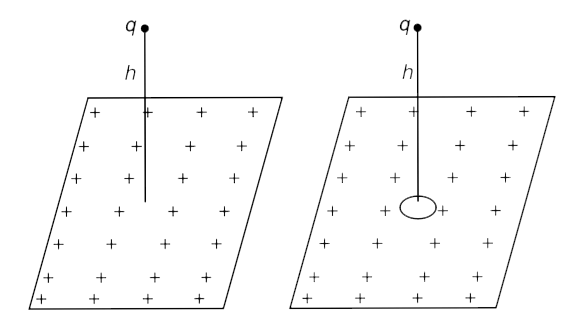
View SolutionA small charged ball is in state of equilibrium at a height h above a large horizontal uniformly charged dielectric plate having surface charge density of σC/m2. (a) Find the acceleration of the ball if a disc of radius r (ltlt h) is removed from the plate directly underneath the ball. (b) Find the terminal speed (V0) acquired by the falling ball. Assume that mass of the ball is m, its radius is x and coefficient of viscosity of air is η. Neglect buoyancy and assume that the ball acquires terminal speed within a short distance of its fall.
View SolutionA particle is thrown with an initial speed v0 at an angle α to the horizontal. Find the radius of curvature r at the highest point of its path, and its ratios to the maximum height H and to the distance L of the particle's flight.
View SolutionA solid uniform sphere resting on a rough horizontal plane is given a horizontal impulse directed through its centre so that it starts sliding with an initial velocity v0. When it finally starts rolling without slipping the speed of its centre is
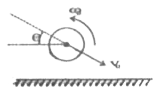
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
View Solution
