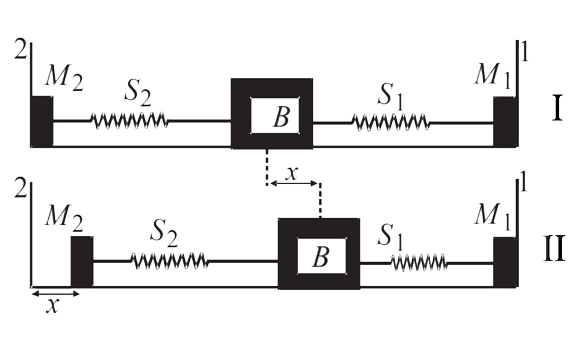
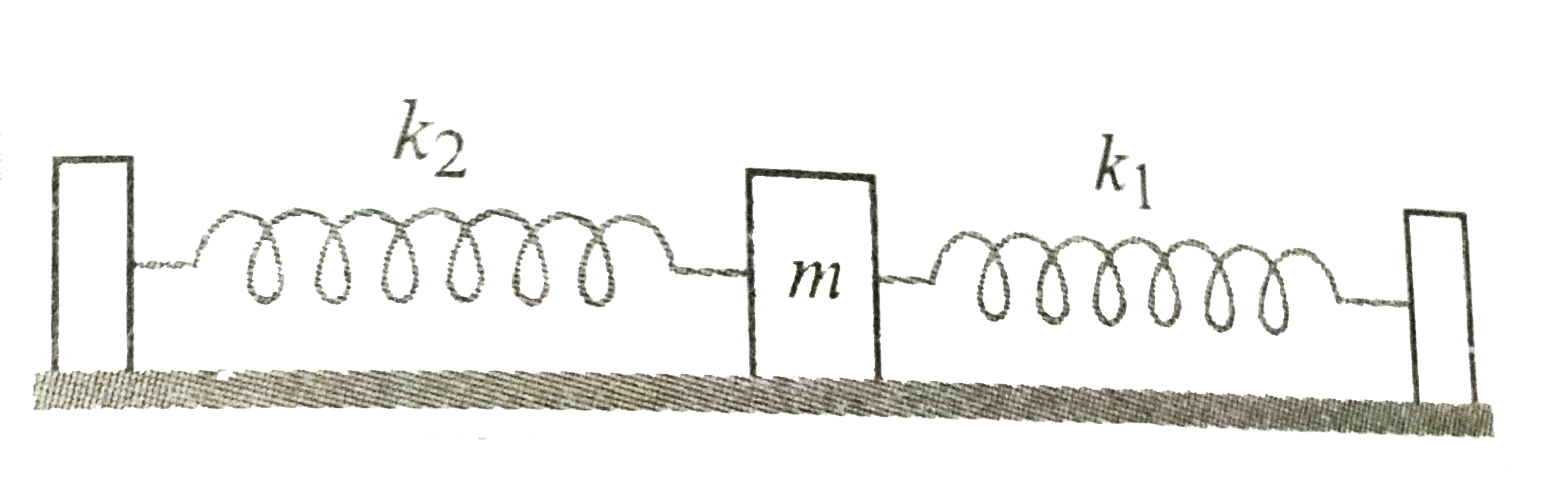
A block is attached to two unstriched sprig and S_(2) with spring constant and , respectively (see fig 1) The other ends are atteched in identical support and not attached in the walls . The springs and supports have negligible mass . There is no friction anywhere . The block is displaced toword wall by a small distance (figure (ii)) and released . THe block return and moves a maximum displacements and are musured with reoact to the equalibrum of the block and the ratio is
4
2
The correct Answer is:C
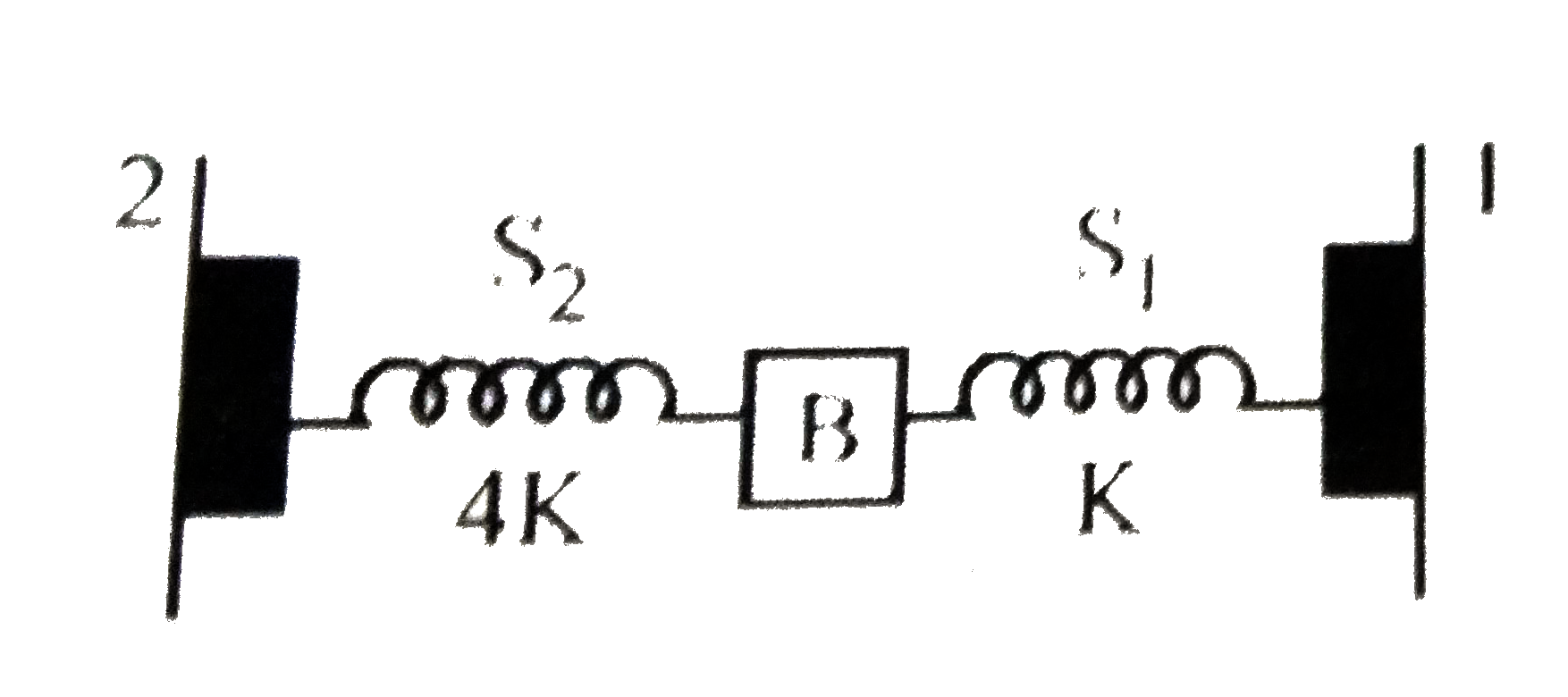
When the block B is moved towards the wall 1, through a dis"tan"ce x, the spring is compressed and the P.E. stored in the spring is increased. It is
When the block B is released, it starts moving towards left, and compresses the spring , through a maximum dis"tan"ce y. The P.E. stored in the spring is
From the principle of conservation of energy
Topper's Solved these Questions
Similar Questions
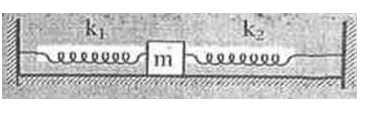
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View Solution
Knowledge Check
A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
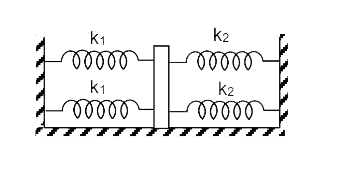 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)mA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
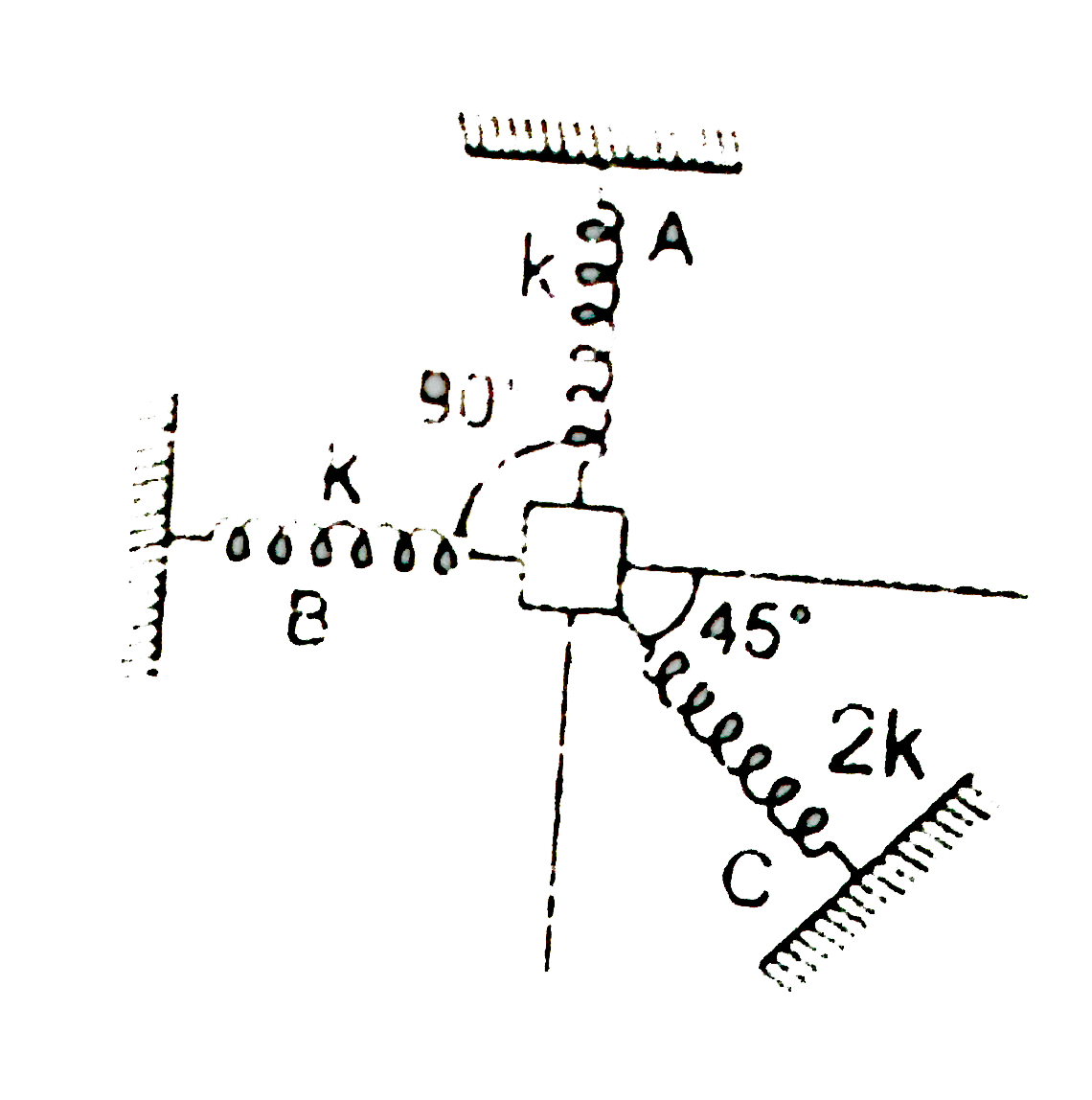
View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
View SolutionA block of mass M1 is attached with a spring constant k. The whole arrangement is placed on a vechile as shown in the figure. If the vehicle starts moving towards right with an acceleration a (there is no friction anywhere), then :
 .
.
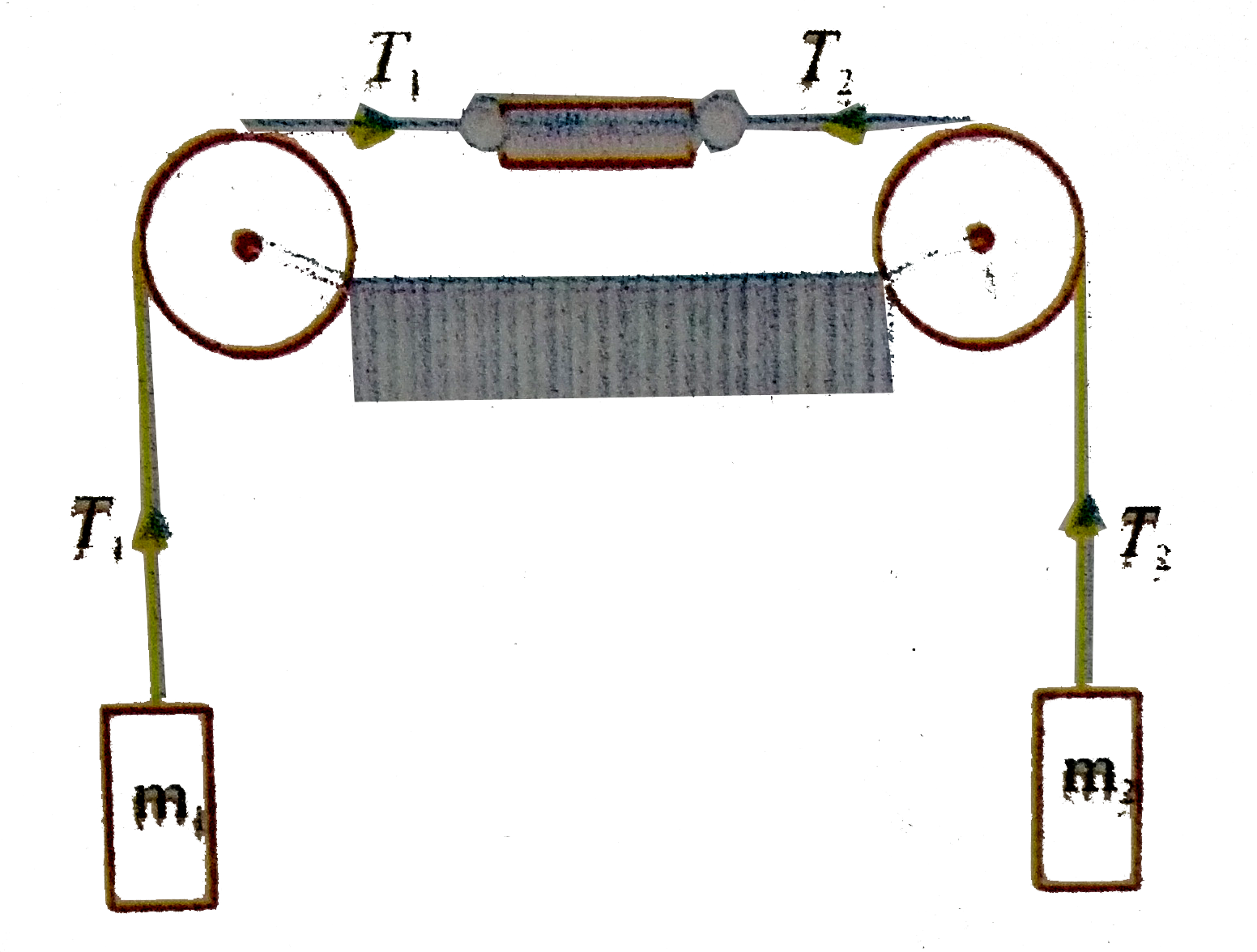
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .
.
View Solution
