A block having mass 'm' and charge q is resting on a frictionless plane at distance L from the wall as shown in fig.Discuss the motion of the block when a uniform electric field E is applied horizontally towards the wall assuming that collision of the block with the wall is perfectly elastic.
To analyze the motion of a block with mass m and charge q resting on a frictionless plane at a distance L from a wall when a uniform electric field E is applied horizontally towards the wall, we can break down the problem into several steps.
1. Identify Forces Acting on the Block:
- The only force acting on the block due to the electric field is the electric force F, which can be calculated as:
F=qE
- This force will cause the block to accelerate towards the wall.
2. Calculate Acceleration:
- Using Newton's second law, the acceleration a of the block can be expressed as:
a=Fm=qEm
3. Determine Motion from Initial Position to Wall:
- When the block is released from rest, it will start moving towards the wall under the influence of the electric force. The distance it travels before hitting the wall is L.
- Using the second equation of motion:
s=ut+12at2
where u=0 (initial velocity), s=L, and a=qEm, we can solve for time t taken to reach the wall:
L=0+12(qEm)t2
Rearranging gives:
t2=2mLqE⇒t=√2mLqE
4. Collision with the Wall:
- The collision with the wall is perfectly elastic, meaning the block will rebound with the same speed but in the opposite direction.
- The velocity v just before hitting the wall can be calculated using:
v=at=qEm√2mLqE=√2qELm
5. Motion After Collision:
- After the collision, the block will move back towards its original position (away from the wall) with the same speed v.
6. Time Taken to Return to Original Position:
- The time taken to return to the original position will be the same as the time taken to reach the wall, which is t=√2mLqE.
7. Determine Total Time Period:
- The total time period T for one complete oscillation (to the wall and back) is:
T=2t=2√2mLqE
8. Conclusion:
- The motion of the block is oscillatory, moving back and forth between the wall and its original position due to the uniform electric field.
- The only force acting on the block due to the electric field is the electric force F, which can be calculated as:
F=qE
- This force will cause the block to accelerate towards the wall.
- Using Newton's second law, the acceleration a of the block can be expressed as:
a=Fm=qEm
- When the block is released from rest, it will start moving towards the wall under the influence of the electric force. The distance it travels before hitting the wall is L.
- Using the second equation of motion:
s=ut+12at2
where u=0 (initial velocity), s=L, and a=qEm, we can solve for time t taken to reach the wall:
L=0+12(qEm)t2
Rearranging gives:
t2=2mLqE⇒t=√2mLqE
- The collision with the wall is perfectly elastic, meaning the block will rebound with the same speed but in the opposite direction.
- The velocity v just before hitting the wall can be calculated using:
v=at=qEm√2mLqE=√2qELm
- After the collision, the block will move back towards its original position (away from the wall) with the same speed v.
- The time taken to return to the original position will be the same as the time taken to reach the wall, which is t=√2mLqE.
- The total time period T for one complete oscillation (to the wall and back) is:
T=2t=2√2mLqE
- The motion of the block is oscillatory, moving back and forth between the wall and its original position due to the uniform electric field.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Describe the motion of the mass m shown in figure. The walls and the block are elastic.
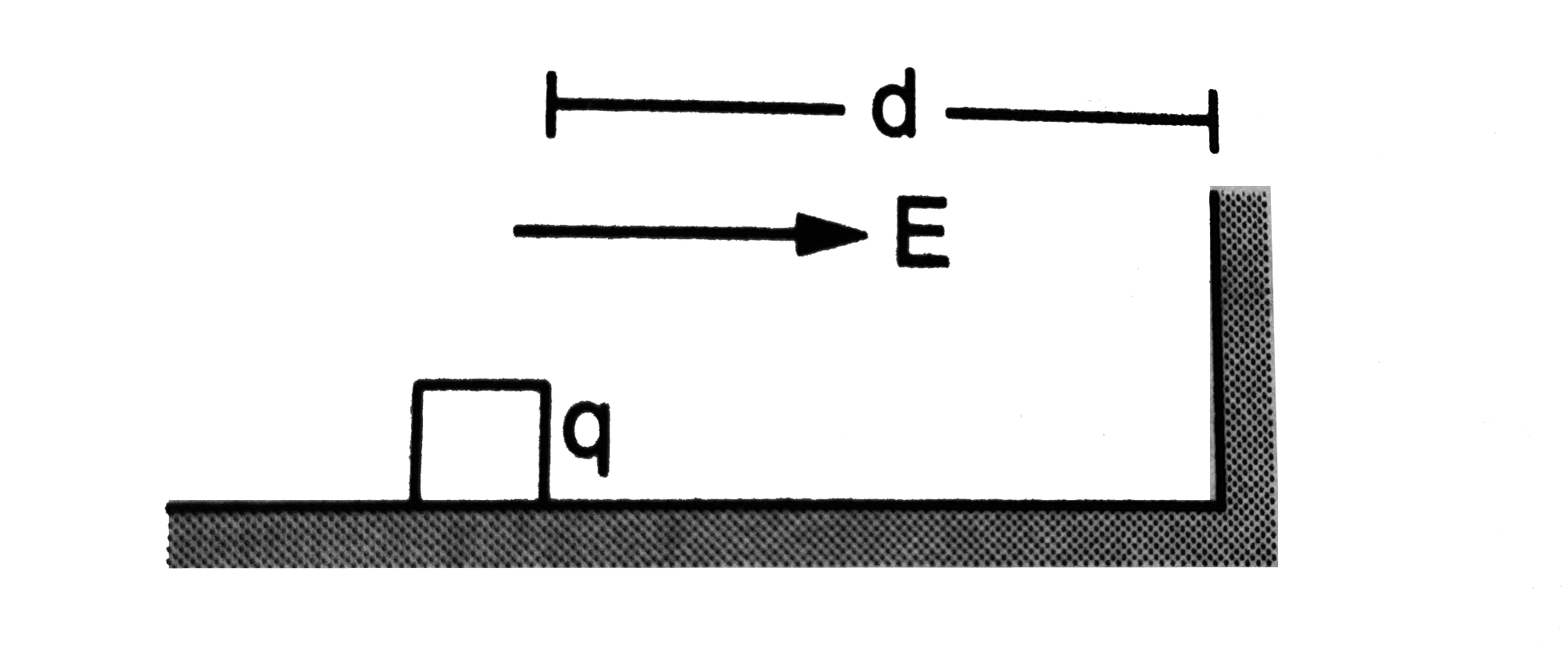
View SolutionA block of mass m containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in figure(29-E2). The distance of the block from the wall is d. A horizontal electric field E to towards right is switched on. Assuming elastic collisions find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
View Solution
Knowledge Check
Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point B immediately after it strikes the second incline is
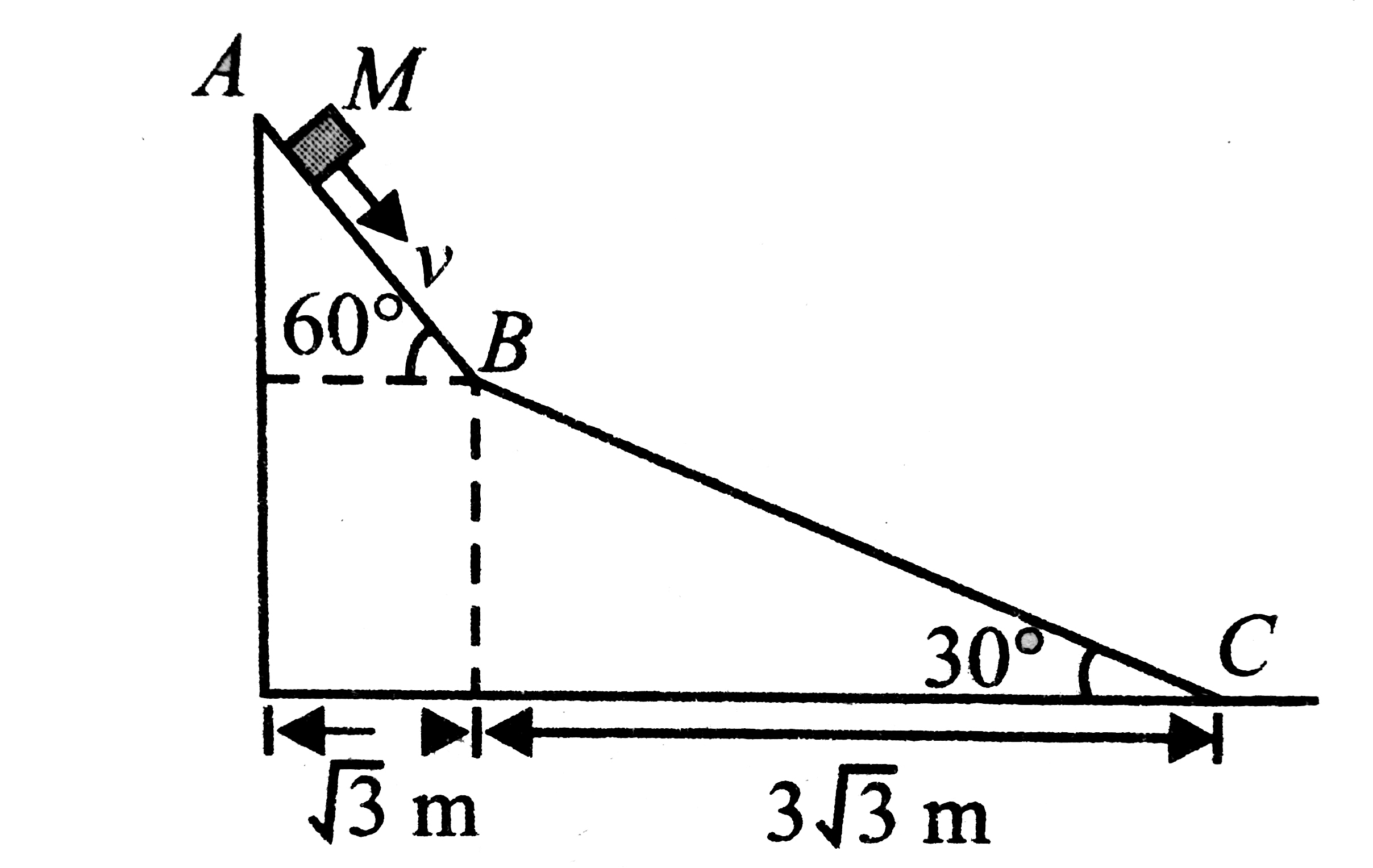 A√60 m/sB√45 m/sC√30 m/sD√15 m/s
A√60 m/sB√45 m/sC√30 m/sD√15 m/s
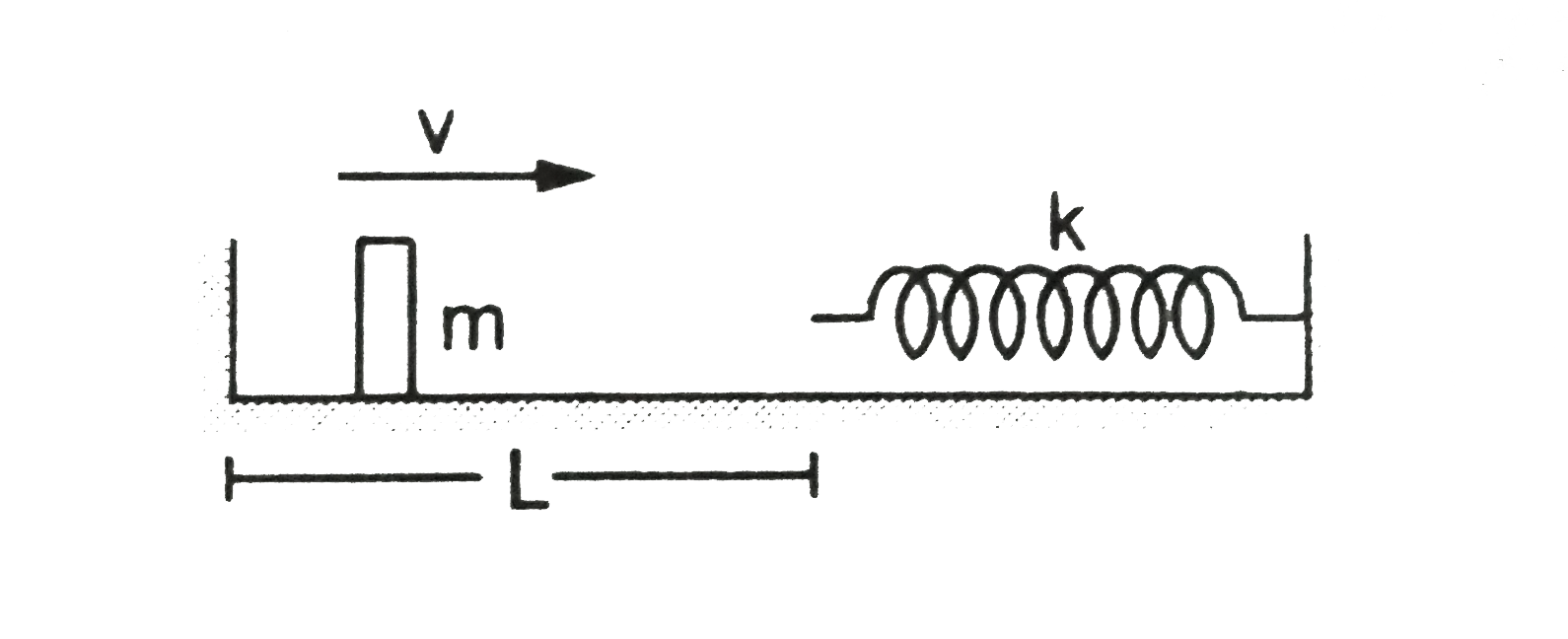
A block of mass 0.9kg attached to a spring of force constant k is lying on a frictionless floor. The spring is compressed to √2cm and the block is at a distance 1/√2cm from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is 0.2sec. Find the approximate value of k

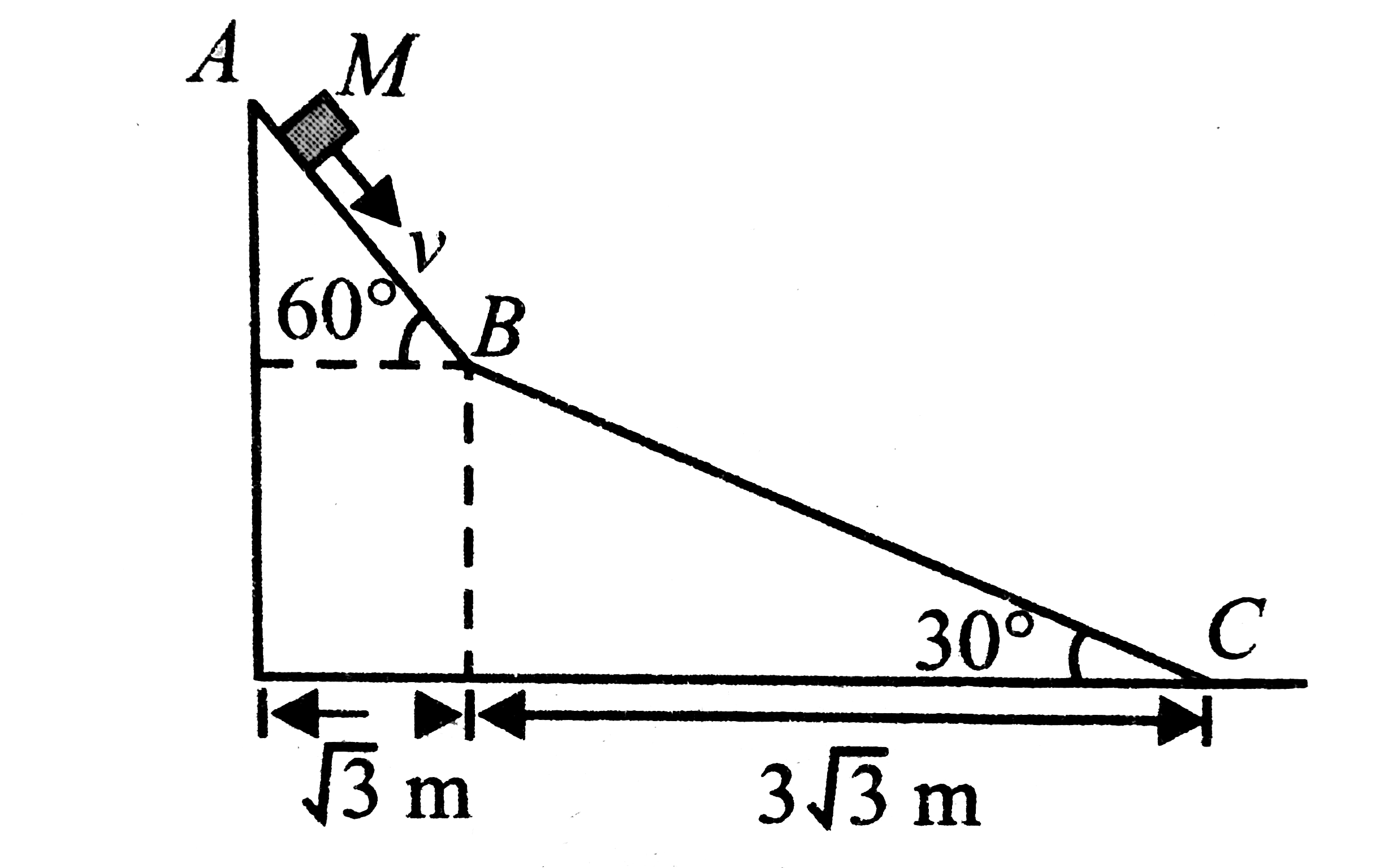
View SolutionA small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
View SolutionA sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.

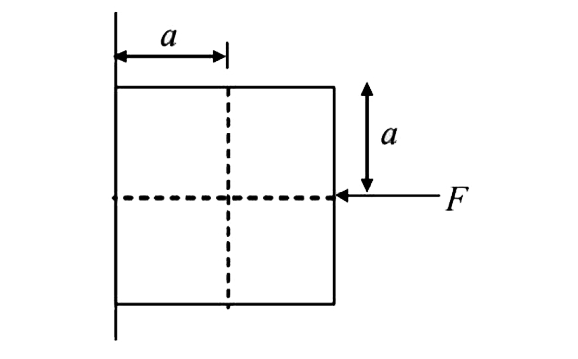
View SolutionA block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
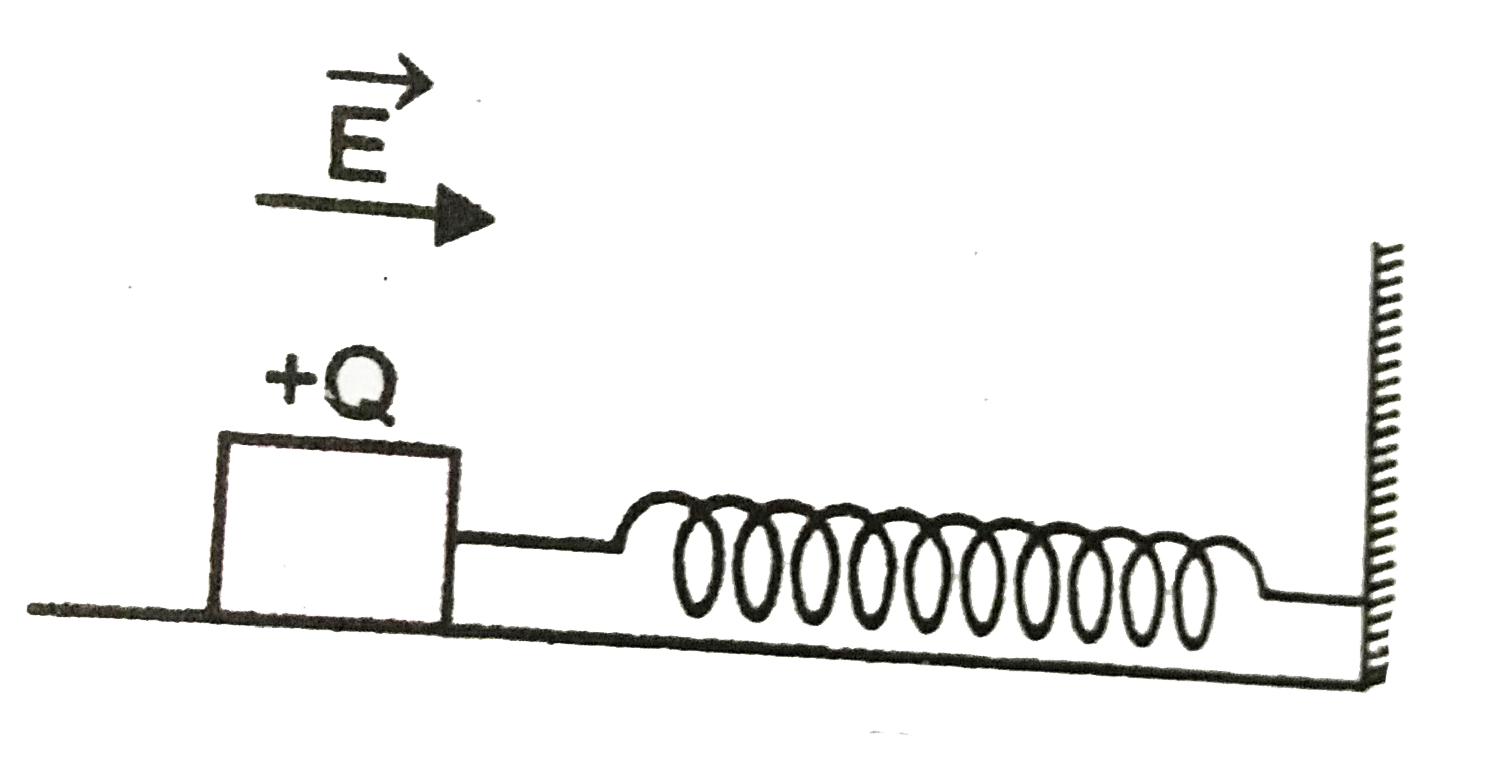
View SolutionA wooden block performs SHM on a frictionless surface with frequency, v0. The block carries a charge +Q on its surface. If now a uniform electric field →E is switched on as shwon in figure., then the SHM of the block will be
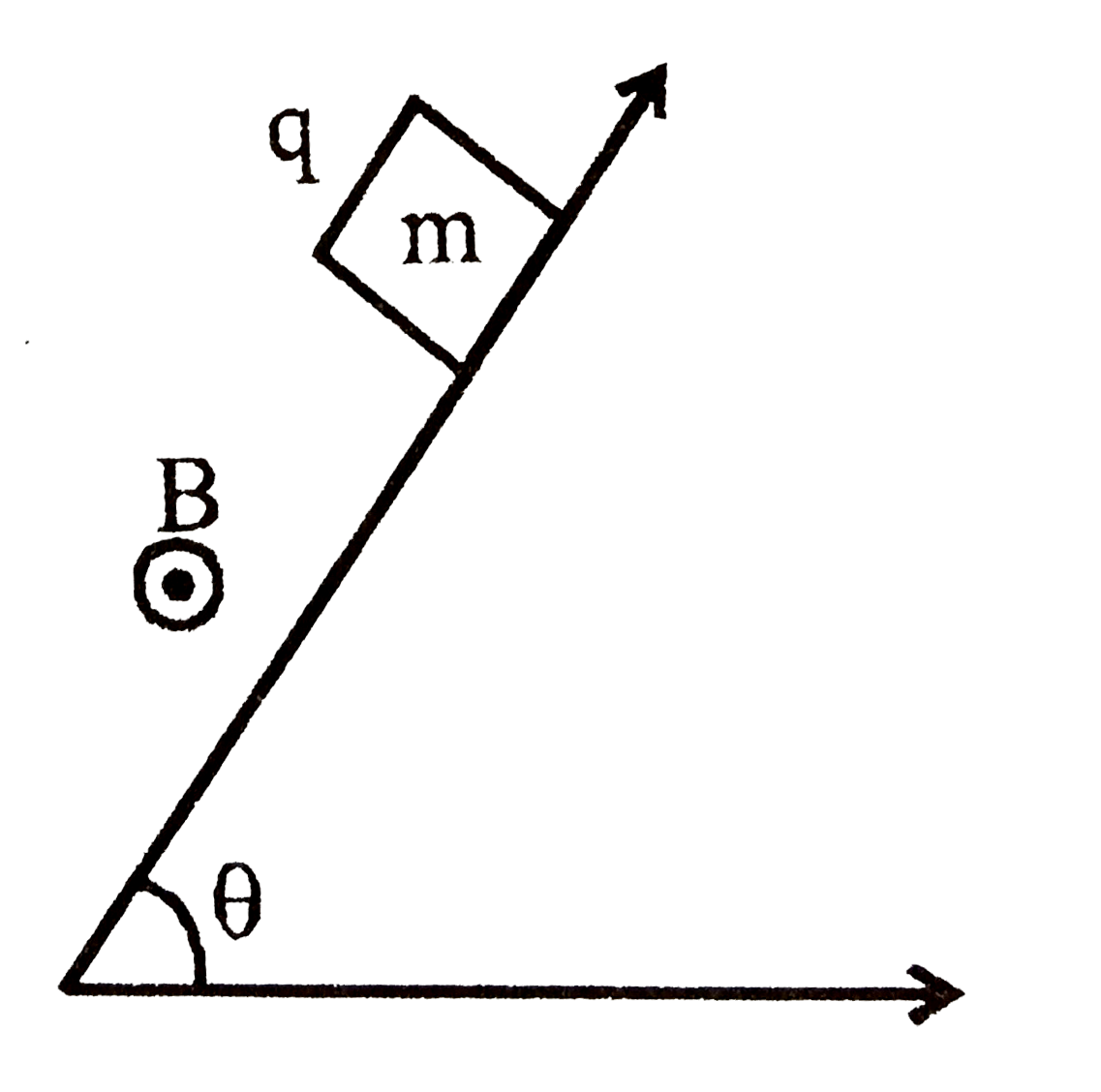
View SolutionA block of mass m & charge q is released on a long smooth inclined plane magnetic field B is constant, unifrom, horizontal and parallel to surface a shown Find the time from start when block loses contact with the surface
 .
.
View Solution
