A parallel plate capacitor has 91 plates, all are identical and arranged with same spacing between them. If the capacitance between adjacent plates is 3 pF. What will be the resultant capacitance?
273 pF
30 pF
94 pF
270 pF
The correct Answer is:D
To solve the problem of finding the resultant capacitance of a parallel plate capacitor with 91 plates, we can follow these steps:
1. Understanding the Configuration:
- A parallel plate capacitor consists of two plates. In this case, we have 91 plates arranged in parallel.
- Each adjacent pair of plates forms a capacitor.
2. Determining the Number of Capacitors:
- If there are 91 plates, the number of capacitors formed between adjacent plates is given by the formula:
Number of Capacitors=Number of Plates−1
- Therefore, the number of capacitors is:
91−1=90
3. Given Capacitance of Each Capacitor:
- The capacitance between each pair of adjacent plates is given as:
C=3 pF
4. Calculating the Total Capacitance:
- Since all capacitors are in parallel, the total capacitance Ctotal is the sum of the capacitances of all the individual capacitors:
Ctotal=C1+C2+C3+…+C90
- Since each capacitor has the same capacitance, we can simplify this to:
Ctotal=90×C
- Substituting the value of C:
Ctotal=90×3 pF=270 pF
5. Final Result:
- The resultant capacitance of the system is:
Ctotal=270 pF
Conclusion:
The resultant capacitance of the parallel plate capacitor with 91 plates, where the capacitance between adjacent plates is 3 pF, is 270 pF.
---
- A parallel plate capacitor consists of two plates. In this case, we have 91 plates arranged in parallel.
- Each adjacent pair of plates forms a capacitor.
- If there are 91 plates, the number of capacitors formed between adjacent plates is given by the formula:
Number of Capacitors=Number of Plates−1
- Therefore, the number of capacitors is:
91−1=90
- The capacitance between each pair of adjacent plates is given as:
C=3 pF
- Since all capacitors are in parallel, the total capacitance Ctotal is the sum of the capacitances of all the individual capacitors:
Ctotal=C1+C2+C3+…+C90
- Since each capacitor has the same capacitance, we can simplify this to:
Ctotal=90×C
- Substituting the value of C:
Ctotal=90×3 pF=270 pF
- The resultant capacitance of the system is:
Ctotal=270 pF
The resultant capacitance of the parallel plate capacitor with 91 plates, where the capacitance between adjacent plates is 3 pF, is 270 pF.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Knowledge Check
A parallel plate capacitor is made by stacking n equally spaced plates connected alternatively. If the capacitance between any two adjacent plates is 'C' then the resultant capacitance is
AnCBCnC(n+1)CD(n−1)CA parallel plate capacitor has a uniform electric field E in the space between the the plates. If the distance between the plates is d and area of each plate is A, the energy stored in the capacitor is
A12ε0E2BE2Adε0C12ε0E2AdDeisi0E2AdAs the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
A parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them.
X has air between the plates while Y contains a dielectric medium of er=4
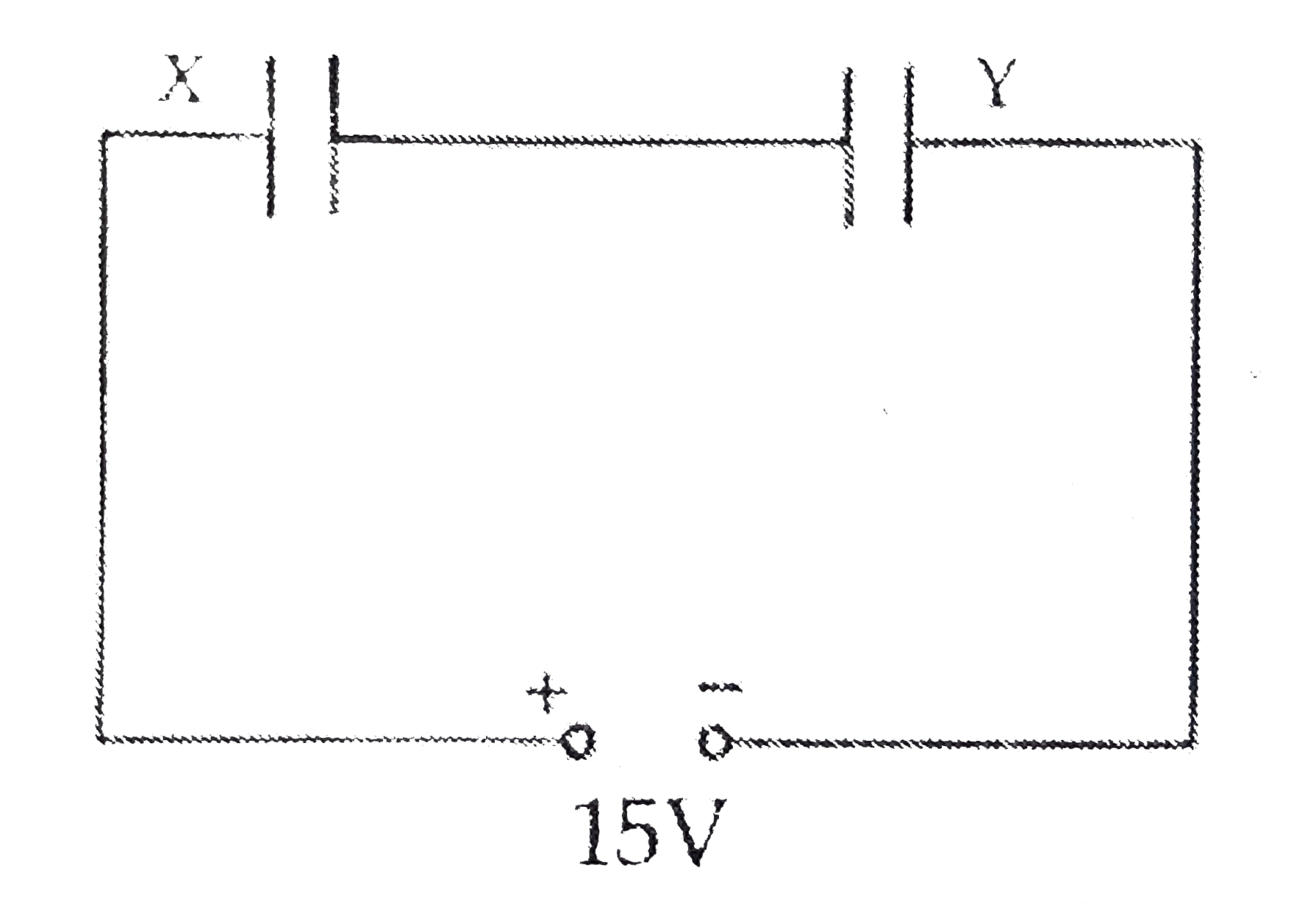
(i) Calculate capacitance of aech capacitor if equivalent capacitance of the combination is 4μF
(ii) Calculate the potential difference between the plates of X and Y
(iii) Estimate the ratio of electrostatic energy stored in X and Y .
View SolutionDerive an expression for the capacitance of a parallel plate capacitor in terms of the areas of the plates and the distance between them. Assume there is a vacuum in between the plates with the electric field between the plates E=σε0 (where the symbols have their usual meaning).
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

View Solution
