An electron of mass initially at rest moves through a certain distance in a uniform electric field in time . A proton of mass also initially at rest takes time to move through an equal distance in this uniform electric field.Neglecting the effect of gravity, the ratio of is nearly equal to
1
The correct Answer is:B
To solve the problem, we need to analyze the motion of the electron and the proton in a uniform electric field. Let's break it down step by step.
Step 1: Understanding the Forces
Both the electron and the proton experience an electric force when placed in a uniform electric field E. The force F acting on each particle can be expressed as:
- For the electron:
Fe=eE
- For the proton:
Fp=eE
where e is the charge of the electron and proton (equal in magnitude).
Step 2: Calculating Accelerations
The acceleration a of each particle can be found using Newton's second law, F=ma:
- For the electron:
ae=Feme=eEme
- For the proton:
ap=Fpmp=eEmp
Step 3: Using the Kinematic Equation
Since both particles start from rest and travel the same distance s, we can use the kinematic equation:
s=12at2
For the electron:
s=12aet21⟹s=12(eEme)t21
For the proton:
s=12apt22⟹s=12(eEmp)t22
Step 4: Setting the Equations Equal
Since both expressions for s are equal, we can set them equal to each other:
12(eEme)t21=12(eEmp)t22
The 12 and eE terms cancel out:
t21me=t22mp
Step 5: Rearranging for the Ratio
Rearranging the equation gives:
t22t21=mpme
Taking the square root of both sides yields:
t2t1=√mpme
Final Answer
Thus, the ratio t2t1 is nearly equal to:
t2t1=√mpme
Both the electron and the proton experience an electric force when placed in a uniform electric field E. The force F acting on each particle can be expressed as:
- For the electron:
Fe=eE
- For the proton:
Fp=eE
where e is the charge of the electron and proton (equal in magnitude).
The acceleration a of each particle can be found using Newton's second law, F=ma:
- For the electron:
ae=Feme=eEme
- For the proton:
ap=Fpmp=eEmp
Since both particles start from rest and travel the same distance s, we can use the kinematic equation:
s=12at2
For the electron:
s=12aet21⟹s=12(eEme)t21
For the proton:
s=12apt22⟹s=12(eEmp)t22
Since both expressions for s are equal, we can set them equal to each other:
12(eEme)t21=12(eEmp)t22
The 12 and eE terms cancel out:
t21me=t22mp
Rearranging the equation gives:
t22t21=mpme
Taking the square root of both sides yields:
t2t1=√mpme
Thus, the ratio t2t1 is nearly equal to:
t2t1=√mpme
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View SolutionAn object of mass m, initially at rest under the action of a constant force F attains a velocity v in time t. Then, the average power supplied to mass is
View Solution
Knowledge Check
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.9×10−9s
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
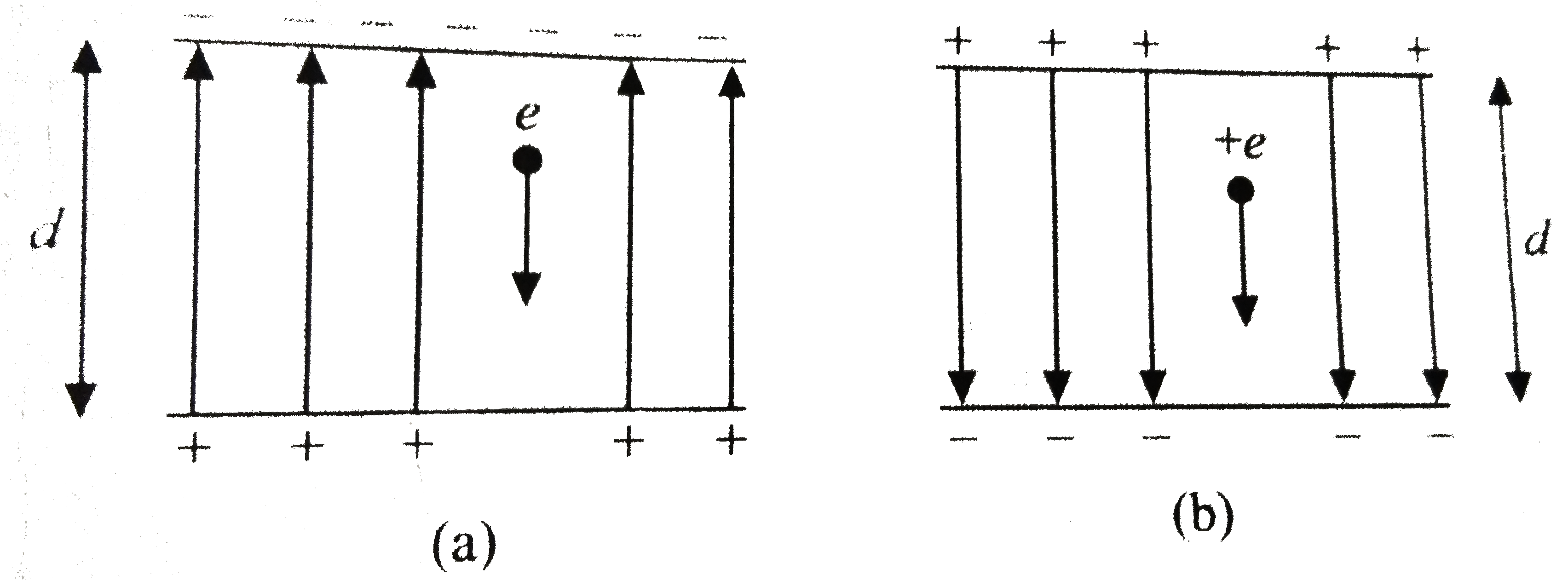 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionIn a region of uniform electric field ofn intencity E, an electron of mass me is released from rest. The distance travelled by the eloctron in a time t is
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron of mass m and charge e initially at rest gets accelerated by a constant electric field E. The rate of change of de-Broglie wavelength of this electron at time t ignoring relativistic effects is
View SolutionA proton and an α-particle start from rest in a uniform electric field, then the ratio of times of flight to travel same distance in the field is
View SolutionAn electron having charge 'e' and mass 'm' is moving a uniform electric field E. Its acceleration will be
View Solution
