A block of mass 2 kg is pushed against a rough vertical wall with a force of 40N. Coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
To determine whether the block will move and in which direction, we will analyze the forces acting on it step by step.
Step 1: Identify the forces acting on the block
- The block has a mass of m=2kg.
- The gravitational force (weight) acting on the block is given by:
W=m⋅g=2kg⋅10m/s2=20N
- A force of F1=40N is applied against the wall, creating a normal force N equal to this force:
N=40N
- A horizontal force F2=15N is applied parallel to the wall.
Step 2: Calculate the maximum static friction force
- The coefficient of static friction μs=0.5.
- The maximum static friction force fmax can be calculated using:
fmax=μs⋅N=0.5⋅40N=20N
Step 3: Analyze the vertical forces
- The vertical forces acting on the block are:
- Weight W=20N acting downward.
- The static friction force f acting upward (if it is sufficient to prevent motion).
- For the block to remain stationary, the static friction must balance the weight:
f≥W⟹f≥20N
- Since the maximum static friction force fmax=20N, it can balance the weight exactly.
Step 4: Analyze the horizontal forces
- The horizontal forces acting on the block are:
- The applied force F2=15N acting to the right.
- The friction force f acting to the left (if it is not exceeded).
- The static friction force can only provide a maximum of 20N to the left.
Step 5: Determine if the block will move
- The applied force F2=15N is less than the maximum static friction force fmax=20N.
- Therefore, the static friction force will be sufficient to prevent the block from moving.
Conclusion
Since the static friction can balance the applied horizontal force, the block will not move. The frictional force exerted by the wall on the block will be equal to the applied force:
f=15N
- The block has a mass of m=2kg.
- The gravitational force (weight) acting on the block is given by:
W=m⋅g=2kg⋅10m/s2=20N
- A force of F1=40N is applied against the wall, creating a normal force N equal to this force:
N=40N
- A horizontal force F2=15N is applied parallel to the wall.
- The coefficient of static friction μs=0.5.
- The maximum static friction force fmax can be calculated using:
fmax=μs⋅N=0.5⋅40N=20N
- The vertical forces acting on the block are:
- Weight W=20N acting downward.
- The static friction force f acting upward (if it is sufficient to prevent motion).
- For the block to remain stationary, the static friction must balance the weight:
f≥W⟹f≥20N
- Since the maximum static friction force fmax=20N, it can balance the weight exactly.
- The horizontal forces acting on the block are:
- The applied force F2=15N acting to the right.
- The friction force f acting to the left (if it is not exceeded).
- The static friction force can only provide a maximum of 20N to the left.
- The applied force F2=15N is less than the maximum static friction force fmax=20N.
- Therefore, the static friction force will be sufficient to prevent the block from moving.
Since the static friction can balance the applied horizontal force, the block will not move. The frictional force exerted by the wall on the block will be equal to the applied force:
f=15N
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.1
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block of mass 2 kg is pushed against a rough vertical wall with a force is 40 N. Coefficient of static friction being 0.5. Another horizontal force is 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
View SolutionA block of mass 1kg is pushed against a rough vertical wall with a force of 20N, coefficient of static friction being 14 Another horizontal force of 10N is applied on the block in a direction parallel to the wall. Will the block move? If yes, in which direction ? If no, find the frictional force exerted by the wall on the block. (g=10m/s2)
View SolutionA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View SolutionA block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
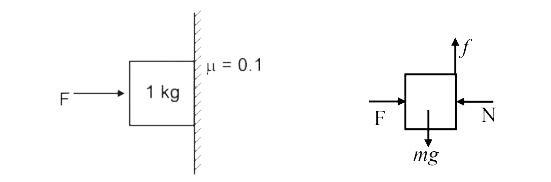
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. If the coefficient of static & kinetic friction are 0.4 & 0.3, the frictional force acting on the block is: (g=10ms−2)
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of mass 2 kg is pressed against a rigid vertical wall by a horizontal force of 100 N. If co-efficient of static and kinetic friction are each equal to 0.3 then find the magnitude and direction of frictional force on the block.

View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View Solution
