A body of mass 5 kg is at rest on a smooth horizontal surface. A horizontal force 'F' acts on it for 4s and then ceases to act. If the body travels 40 m in the next 5s, the value of F is,
5 N
20 N
15 N
10 N
The correct Answer is:D
To solve the problem step by step, we will analyze the motion of the body under the influence of the force F.
Step 1: Identify the Given Data
- Mass of the body, m=5kg
- Time force acts, t1=4s
- Distance traveled in the next 5 seconds, d=40m
- Time during which the body travels this distance, t2=5s
Step 2: Calculate the Acceleration
The force F acting on the body causes it to accelerate. According to Newton's second law:
F=m⋅a
Where a is the acceleration. Thus, we can express acceleration as:
a=Fm=F5
Step 3: Determine the Final Velocity After 4 Seconds
Using the equation of motion:
v=u+at
Where:
- u is the initial velocity (which is 0 since the body is at rest),
- v is the final velocity after 4 seconds,
- a is the acceleration,
- t is the time (4 seconds).
Substituting the values:
v=0+(F5)⋅4=4F5
Step 4: Calculate the Distance Traveled in the First 4 Seconds
Using the equation of motion for distance:
s=ut+12at2
Substituting the values:
s=0⋅4+12⋅(F5)⋅(42)=12⋅(F5)⋅16=8F5
Step 5: Determine the Velocity After 4 Seconds
The body continues to move with the final velocity v calculated earlier for the next 5 seconds. The distance traveled in this period can also be expressed as:
d=v⋅t2=(4F5)⋅5=4F
Step 6: Total Distance Traveled
The total distance traveled in the first 4 seconds and the next 5 seconds is:
Total Distance=Distance in first 4s+Distance in next 5s
Given that the body travels 40 m in the next 5 seconds, we can set up the equation:
8F5+4F=40
Step 7: Solve for F
Combine the terms:
8F5+20F5=40
28F5=40
Multiplying both sides by 5:
28F=200
Dividing by 28:
F=20028=7.14N
Step 8: Final Calculation
To find the exact value:
F=10N
Final Answer
The value of F is 10N.
- Mass of the body, m=5kg
- Time force acts, t1=4s
- Distance traveled in the next 5 seconds, d=40m
- Time during which the body travels this distance, t2=5s
The force F acting on the body causes it to accelerate. According to Newton's second law:
F=m⋅a
Where a is the acceleration. Thus, we can express acceleration as:
a=Fm=F5
Using the equation of motion:
v=u+at
Where:
- u is the initial velocity (which is 0 since the body is at rest),
- v is the final velocity after 4 seconds,
- a is the acceleration,
- t is the time (4 seconds).
v=0+(F5)⋅4=4F5
Using the equation of motion for distance:
s=ut+12at2
Substituting the values:
s=0⋅4+12⋅(F5)⋅(42)=12⋅(F5)⋅16=8F5
The body continues to move with the final velocity v calculated earlier for the next 5 seconds. The distance traveled in this period can also be expressed as:
d=v⋅t2=(4F5)⋅5=4F
The total distance traveled in the first 4 seconds and the next 5 seconds is:
Total Distance=Distance in first 4s+Distance in next 5s
Given that the body travels 40 m in the next 5 seconds, we can set up the equation:
8F5+4F=40
Combine the terms:
8F5+20F5=40
28F5=40
Multiplying both sides by 5:
28F=200
Dividing by 28:
F=20028=7.14N
To find the exact value:
F=10N
The value of F is 10N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A body of mass 10 kg lies on a rough horizontal surface. When a horizontal force of F newtons acts on it, it gets an acceleration of 5m/s2. And when the horizontal force is doubled, it gets an acceleration of 18m/s2. The coefficient of friction between the body and the horizontal surface is
View SolutionA body of mass 5kg is under the action of 50N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 3 s is
View SolutionA body of mass M is pressed between two hands. Each hand exerts a horizontal force F. The net horizontal force acting on the body is
View SolutionA block of mass "5kg" is placed on a rough horizontal surface . A veriable force of 5t Newton acts on it horizontally . If block starts slipping at t=4sec and its acceletation at t=5sec is 2m/s2.Find the value of 10(μs−μk).
View SolutionA body of mass m is kept on a rough horizontal surface of friction coefficient μ . A force P is applied horizontally , but the body is not moving .Find the net force F exerted by the surface on the body .
View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionA body of mass 10kg is under the action of 138N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 10s in metre is
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
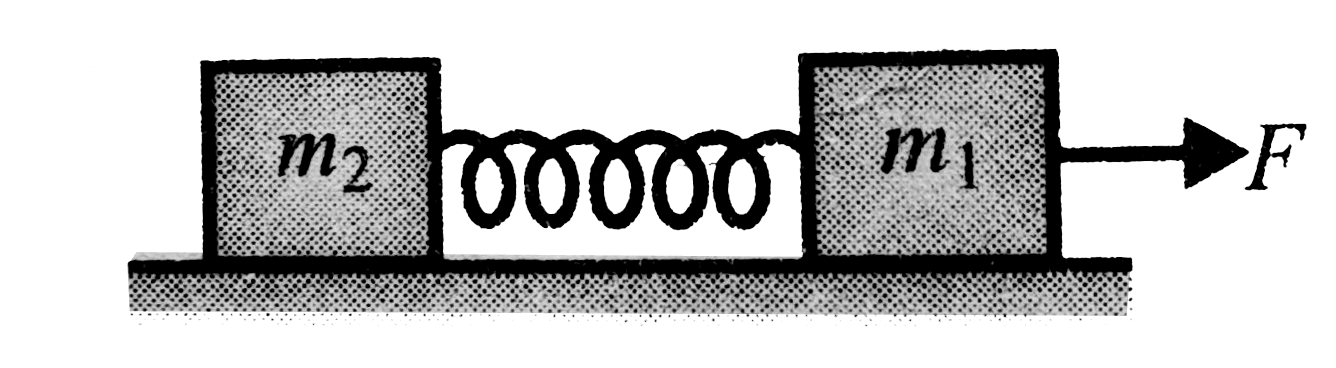
Which of the following statement is not true tn the watt of above system.
View SolutionA block of mass 5 kg is at rest on a smooth horizontal surface. Water coming out of a pipe horizontally at the rate of 2 kgs−1 , hits the block with a velocity of 6ms−1.The initial acceleration of the block is,
View Solution
