A body of mass m is attached ot one end of a massless spring which is suspended vertically form a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation?
(b) Find the frequency of oscillation?
(a) when the support of the hand is removed, the body oscillates about a mean position.
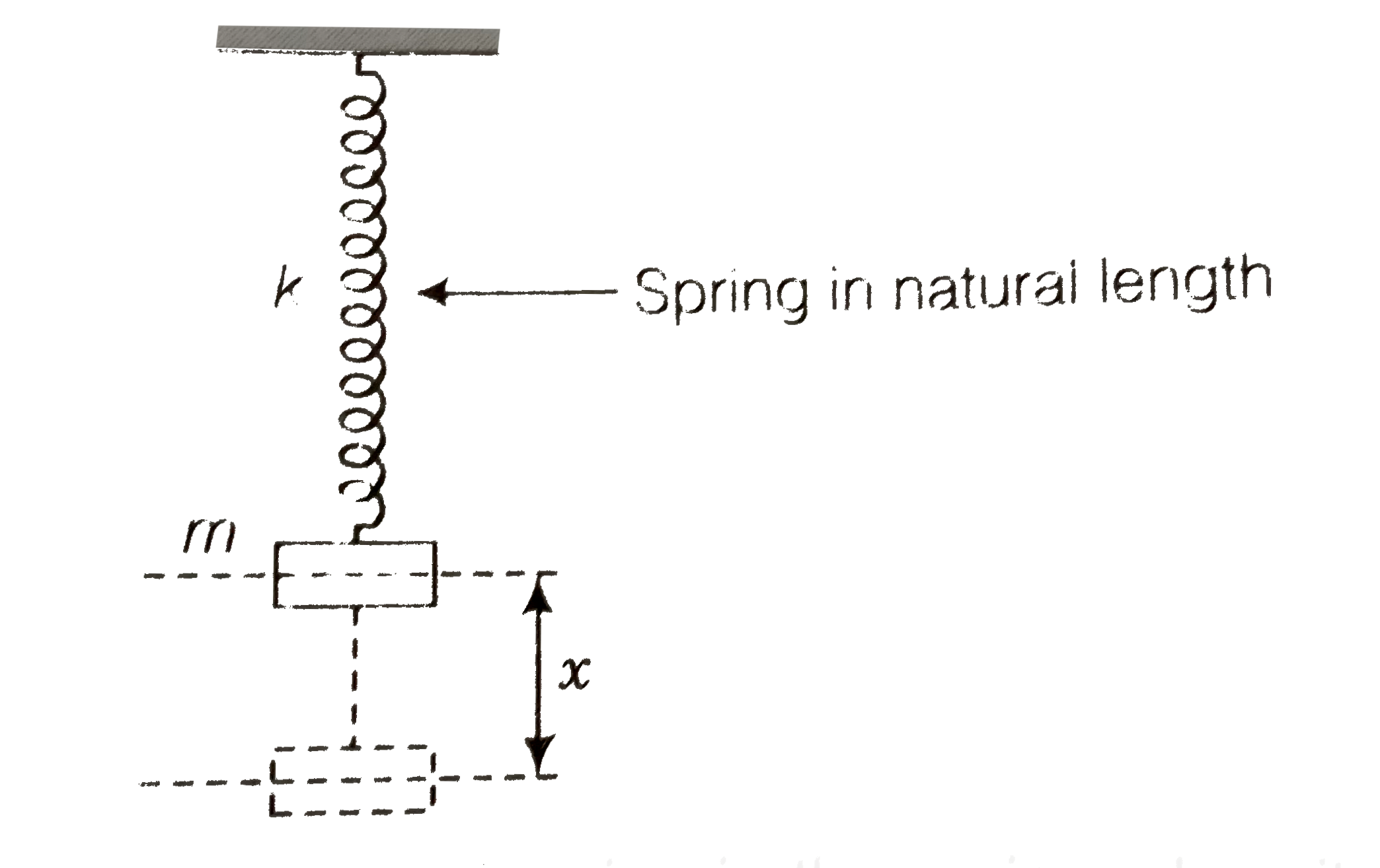
Suppose x is the maximum extension in the spring when it reaches the lowest point in oscillation.
Loss in PE of the block =mgx
where, m=mass of the block .....(i)
Gain in elastic potential energy of the spring
=12kx2 .....(ii)
As the two are equal, conservving the mechanical energy.
we get, mgx=12kx2orx=2mgg ....(iii)
Now, the mean position of oscillation will be, when the block is balanced by the spring.
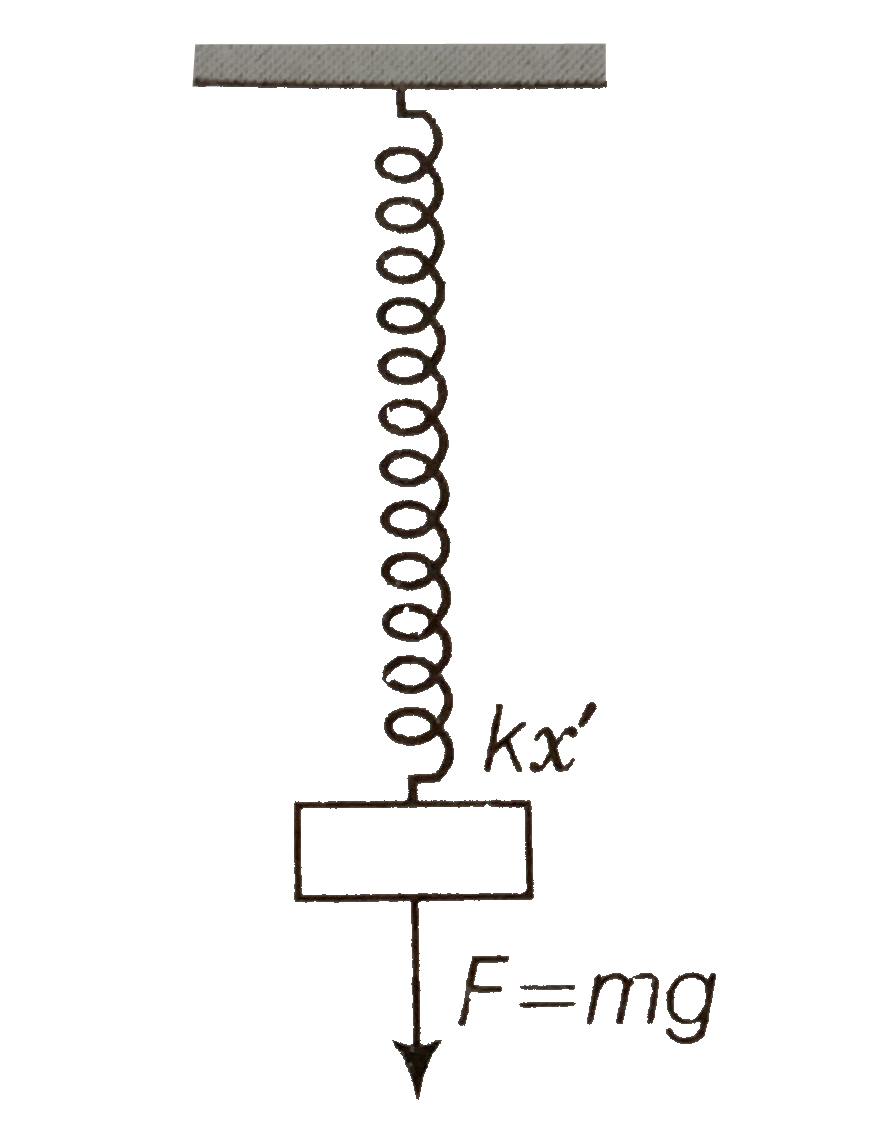
If x' is the extension in that case, then
F=+kx'
But F=mg
⇒mg=+kx'
or x'=mgk .....(iv)
Dividing Eq. (iii) Eq. (iv),
xx'=2mgk/mgk=2
⇒x=2x'
But given x=4 cm (maximum extension from the unstretched position)
∴2x'=4
∴x'=42=2cm
But the displacement of mass from the mean position to the position when spring attains its naural length is equal to amplitude of the oscillation.
∴A=x'=2cm
where, A = amplitude of the motion.
(b) Time period of the oscillating system depends on mass spirng constant given by
T=2π√mk
It does not depend on the amplitude.
But from Eq. (iii),
2mgk=x (maximum extension)
2gmk=4cm=4×10−2cm
∴mk=4×10−22g=2×10−2g
∴mk=g2×10−2
and v=frequency=1T=12π√km
∴v=12×3.14√4.910−2=1628×√4.9×100
=10628×221=3.51Hz.
Note The block during oscillation connot go above the position it was released, as it is given that there is no velocity in the upward direction either by the system or external agent.
Topper's Solved these Questions
Similar Questions
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neigther stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation ?
(b) Find the frequency of oscillation?
View SolutionAn object of mass M oscillating with amplitude 'A' mass 'm' is added at mean position. Find new amplitude of oscillation.
View Solution
Knowledge Check
A mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
A3.1cmB6.2cmC9.3cmD12.4cmA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
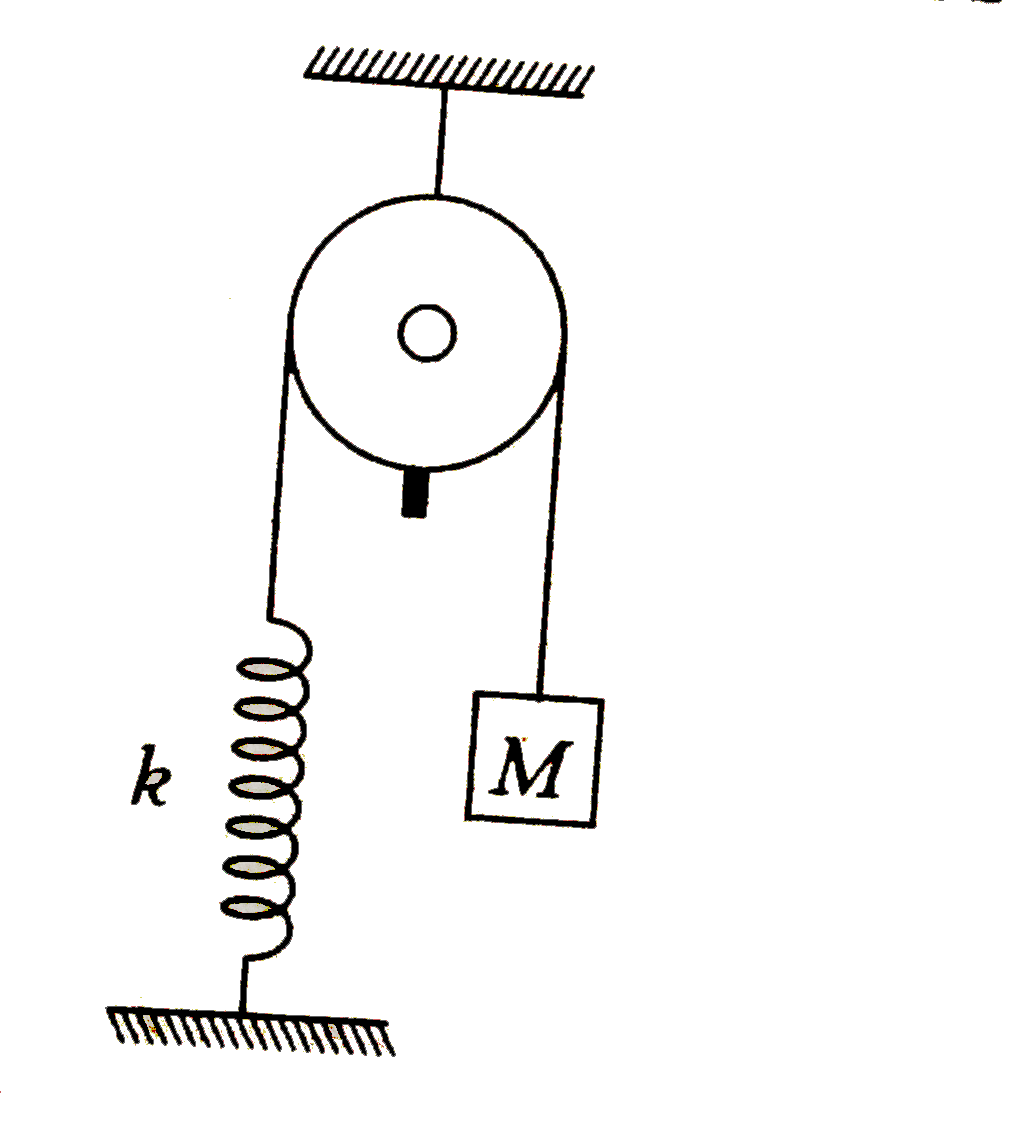 A0.5 mB0.25 mC0.2 mD0.1 m
A0.5 mB0.25 mC0.2 mD0.1 mA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
Amg(l+y)B12mg(l+y)C12mgyDMgy
A mass m=8kg is attached to a spring passing over a pulled whose other end is fixed to ground and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. Find maximum velocity of mass
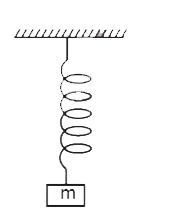
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA mass m suspended from a vertical spring oscillates with a period of 4 s. The mass is then kept at rest. Through what dis"tan"ce the spring will be stretched ? [Take pi^(2)=10]
View SolutionA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View Solution
