Question

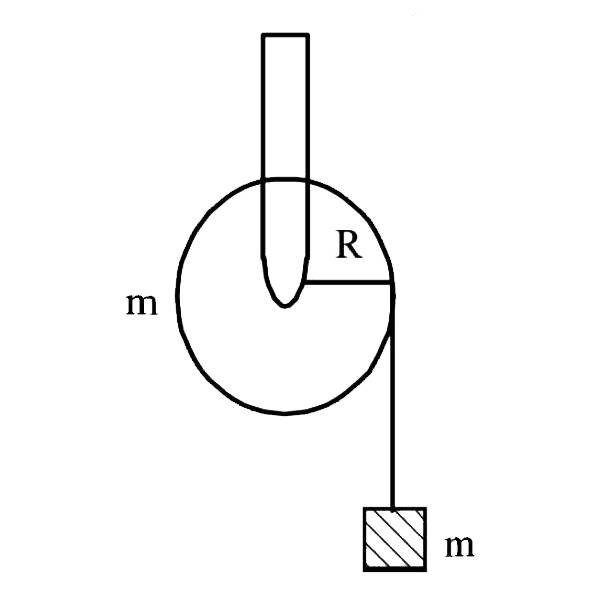
A bucket of mass 8 kg is supported by a light rope wound around a solid wooden cylinder of mass 12 kg and radius 20 cm free to rotate about its axis. A man holding the free end of the rope, with the bucket and the cylinder at rest initially, lets go the bucket freely downwards in a well 50 m deep. Neglecting friction, obtain the speed of the bucket and the angular speed of the cylihder just before the bucket enters water.

Explanation

To solve the problem, we will use the principle of conservation of energy. The initial potential energy of the bucket will be converted into kinetic energy of the bucket and rotational kinetic energy of the cylinder as the bucket falls.

1. Identify the given values:
- Mass of the bucket, \( m_b = 8 \, \text{kg} \)
- Mass of the cylinder, \( m_c = 12 \, \text{kg} \)
- Radius of the cylinder, \( r = 0.2 \, \text{m} \)
- Height of the well, \( h = 50 \, \text{m} \)
- Acceleration due to gravity, \( g = 9.81 \, \text{m/s}^2 \)

2. Calculate the initial potential energy (PE_initial) of the bucket:
\( PE_{\text{initial}} = m_b \cdot g \cdot h = 8 \cdot 9.81 \cdot 50 \)
\( PE_{\text{initial}} = 3924 \, \text{J} \)

3. Set up the energy conservation equation:
The initial potential energy will be equal to the sum of the kinetic energy of the bucket and the rotational kinetic energy of the cylinder just before the bucket enters the water.
\( PE_{\text{initial}} = KE_{\text{bucket}} + KE_{\text{cylinder}} \)
\( 3924 = \frac{1}{2} m_b v^2 + \frac{1}{2} I \omega^2 \)

4. Calculate the moment of inertia (I) of the cylinder:
The moment of inertia for a solid cylinder is given by:
\( I = \frac{1}{2} m_c r^2 = \frac{1}{2} \cdot 12 \cdot (0.2)^2 \)
\( I = \frac{1}{2} \cdot 12 \cdot 0.04 = 0.24 \, \text{kg m}^2 \)

5. Relate the angular velocity (ω) to the linear velocity (v):
The linear velocity of the bucket and the angular velocity of the cylinder are related by:
\( v = r \omega \quad \Rightarrow \quad \omega = \frac{v}{r} \)

6. Substitute ω into the energy equation:
Substitute \( \omega = \frac{v}{r} \) into the kinetic energy of the cylinder:
\( KE_{\text{cylinder}} = \frac{1}{2} I \left(\frac{v}{r}\right)^2 = \frac{1}{2} \cdot 0.24 \cdot \left(\frac{v}{0.2}\right)^2 \)
\( KE_{\text{cylinder}} = \frac{0.24}{2 \cdot 0.04} v^2 = 3 v^2 \)

7. Substitute back into the energy conservation equation:
\( 3924 = \frac{1}{2} \cdot 8 v^2 + 3 v^2 \)
\( 3924 = 4 v^2 + 3 v^2 = 7 v^2 \)
\( v^2 = \frac{3924}{7} \approx 560.57 \)
\( v \approx \sqrt{560.57} \approx 23.7 \, \text{m/s} \)

8. Calculate the angular speed (ω) of the cylinder:
\( \omega = \frac{v}{r} = \frac{23.7}{0.2} \approx 118.5 \, \text{rad/s} \)

Final Answers:
- Speed of the bucket just before entering the water: \( v \approx 23.7 \, \text{m/s} \)
- Angular speed of the cylinder just before the bucket enters the water: \( \omega \approx 118.5 \, \text{rad/s} \)