A bullet fired into a fixed target loses half of its velocity after penetrating 3cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
(a) 2.0cm
(b) 3.0cm
(c) 1.0cm
(d) 1.5cm
The correct Answer is:C
To solve the problem, we will apply the work-energy theorem, which states that the work done on an object is equal to the change in its kinetic energy.
1. Understanding the Initial Conditions:
- Let the initial velocity of the bullet be V.
- After penetrating 3 cm into the target, the bullet's velocity reduces to V2.
2. Applying the Work-Energy Theorem:
- The work done by the resistive force F while the bullet penetrates the target can be expressed as:
W=F⋅S
- The change in kinetic energy as the bullet penetrates 3 cm (0.03 m) is given by:
ΔKE=KEinitial−KEfinal=12mV2−12m(V2)2
- Simplifying the kinetic energy change:
ΔKE=12mV2−12mV24=12mV2(1−14)=12mV2⋅34=38mV2
3. Setting Up the Equation for Work Done:
- The work done by the resistive force over the distance S1=3cm=0.03m is:
W=F⋅S1=F⋅0.03
- According to the work-energy theorem:
F⋅0.03=38mV2
- Rearranging gives:
F=3mV28⋅0.03
4. Finding Further Penetration:
- Now, we need to find how much further the bullet penetrates before coming to rest. Let this additional distance be S2.
- The initial velocity for this phase is V2 and the final velocity is 0.
- The change in kinetic energy for this phase is:
ΔKE=12m(V2)2−0=12mV24=18mV2
- The work done while penetrating S2 is:
W=F⋅S2
- Setting the work done equal to the change in kinetic energy gives:
F⋅S2=18mV2
5. Relating the Two Work Equations:
- From the first part, we have F=3mV28⋅0.03.
- Substitute F into the second equation:
3mV28⋅0.03⋅S2=18mV2
- Cancel mV2 from both sides:
3S28⋅0.03=18
- Rearranging gives:
3S2=0.03⇒S2=0.033=0.01m=1cm
6. Final Answer:
- The bullet will penetrate an additional distance of 1 cm before coming to rest.
- Let the initial velocity of the bullet be V.
- After penetrating 3 cm into the target, the bullet's velocity reduces to V2.
- The work done by the resistive force F while the bullet penetrates the target can be expressed as:
W=F⋅S
- The change in kinetic energy as the bullet penetrates 3 cm (0.03 m) is given by:
ΔKE=KEinitial−KEfinal=12mV2−12m(V2)2
- Simplifying the kinetic energy change:
ΔKE=12mV2−12mV24=12mV2(1−14)=12mV2⋅34=38mV2
- The work done by the resistive force over the distance S1=3cm=0.03m is:
W=F⋅S1=F⋅0.03
- According to the work-energy theorem:
F⋅0.03=38mV2
- Rearranging gives:
F=3mV28⋅0.03
- Now, we need to find how much further the bullet penetrates before coming to rest. Let this additional distance be S2.
- The initial velocity for this phase is V2 and the final velocity is 0.
- The change in kinetic energy for this phase is:
ΔKE=12m(V2)2−0=12mV24=18mV2
- The work done while penetrating S2 is:
W=F⋅S2
- Setting the work done equal to the change in kinetic energy gives:
F⋅S2=18mV2
- From the first part, we have F=3mV28⋅0.03.
- Substitute F into the second equation:
3mV28⋅0.03⋅S2=18mV2
- Cancel mV2 from both sides:
3S28⋅0.03=18
- Rearranging gives:
3S2=0.03⇒S2=0.033=0.01m=1cm
- The bullet will penetrate an additional distance of 1 cm before coming to rest.
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Video
Similar Questions
One mole of a mono-atomic ideal gas is mixed with one mole of a diatomic ideal gas. The molar specific heat of the mixture at constant volume is ……
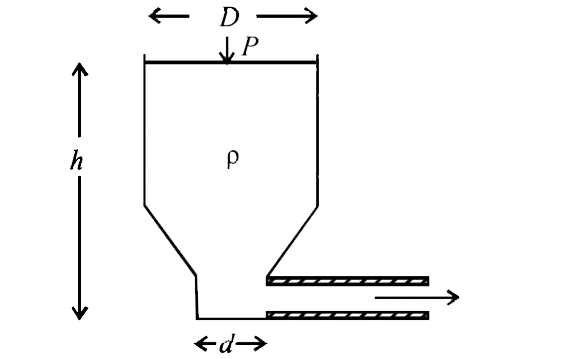
View SolutionShown in the figure is a container whose top and botoom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as ρ. Calculate the coefficient of viscosity η.
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 1cm. How much further it will penetrate before coming to rest, assuming that it faces constant resistance to motion
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 3 cm . How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
View SolutionA bullet fired in to a fixed target tosses half of it's velocity after penetrating distance of 3 cm. How much further it will penetrate before coming to rest assuming that if faces constnat resistance to it's motion?
View SolutionA bullet fired into a target loses half of its velocity after penetrating 36 cm. Further distance covered by it before coming to rest will be
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion ?
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion ?
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion ?
View SolutionA bullet fired into a fixed target loses half of its velocity in penetrating 15 cm. How much further it will penetrate before coming to rest?
View SolutionA bullet fired into a fixed target loses half of its velocity in penetrating 15 cm.How much further it will penetrate before coming to rest?
View SolutionA bullet fired into a fixed targe loses half of its velocity in penetrating 15 cm. How much further it will penetrate before coming to rest?
View SolutionA bullet fired into a fixed targe loses half of its velocity in penetrating 15 cm. How much further it will penetrate before coming to rest?
View SolutionA bullet fired into a fixed target loses half of its velocity in penetrating 15 cm. How much further it will penetrate before coming to rest ?
View SolutionA bullet fired into a fixed target losses half of its velocity after penetrating 5cm. How much further will it penetrate before coming to rest assuming that it faces constant resistance ?
View Solution