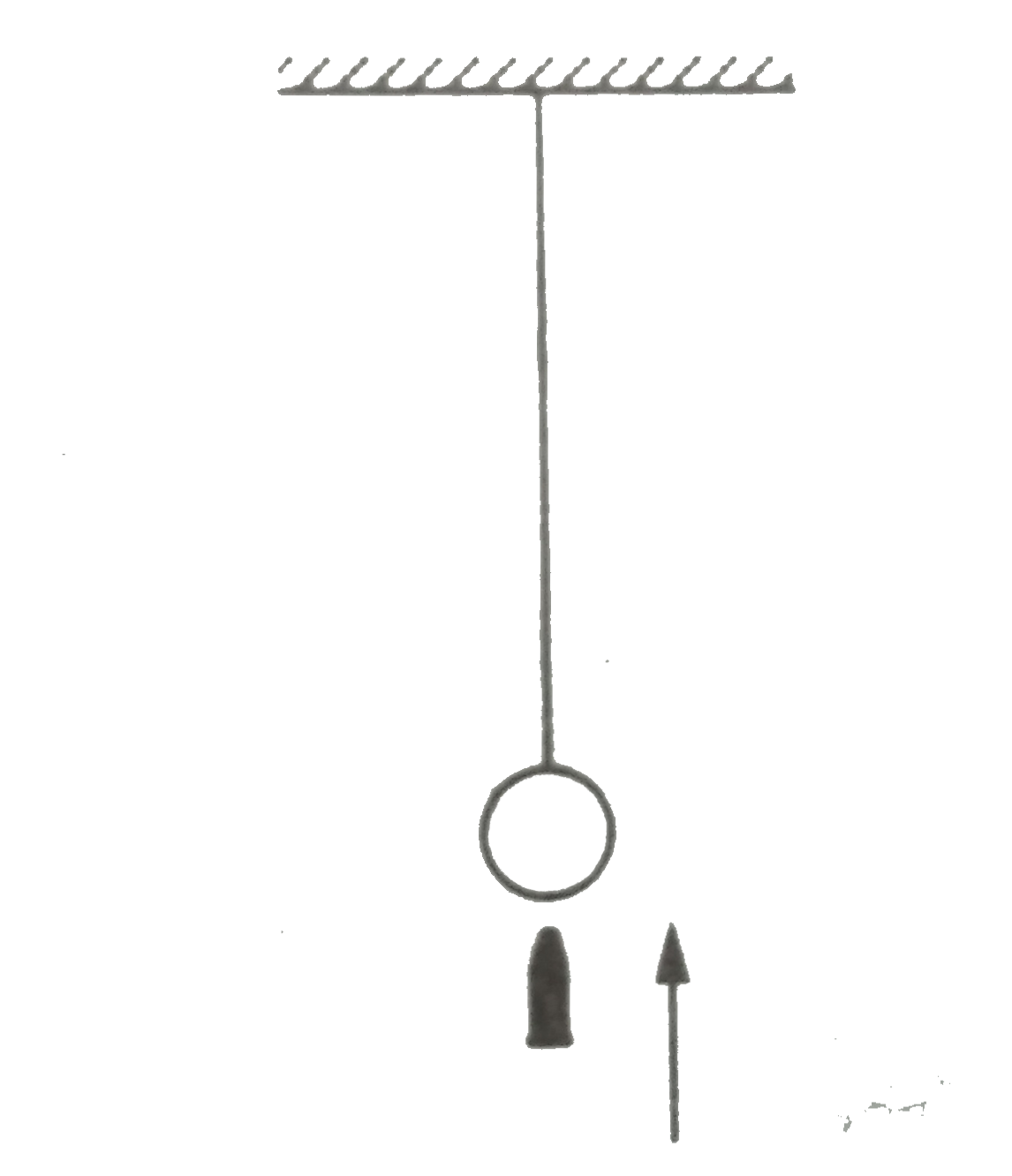
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mas 5.0 kg and gets embedded in it figure. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
To solve the problem step by step, we will use the principles of conservation of momentum and conservation of energy.
Step 1: Convert the mass of the bullet and pendulum to kilograms
- Mass of the bullet, m=25g=0.025kg
- Mass of the pendulum, M=5.0kg
Hint: Always convert units to SI units for consistency in calculations.
Step 2: Identify the vertical displacement
- The vertical displacement of the pendulum, h=10cm=0.1m
Hint: Ensure that all measurements are in meters when applying formulas related to energy and motion.
Step 3: Apply conservation of momentum
When the bullet embeds itself into the pendulum, we can apply the conservation of momentum:
mu=(M+m)v
Where:
- u is the initial speed of the bullet,
- v is the speed of the pendulum and bullet just after the collision.
Rearranging gives:
v=mM+mu
Hint: Remember that momentum before the collision equals momentum after the collision.
Step 4: Apply conservation of energy
After the collision, the kinetic energy of the bullet and pendulum system is converted into potential energy as the pendulum rises:
12(M+m)v2=(M+m)gh
Where:
- g is the acceleration due to gravity (approximately 10m/s2).
We can simplify this equation:
12v2=gh
Hint: The potential energy at the highest point is equal to the kinetic energy just after the collision.
Step 5: Substitute v in the energy equation
Substituting v=mM+mu into the energy equation:
12(mM+mu)2=gh
This leads to:
12m2(M+m)2u2=gh
Step 6: Solve for u2
Rearranging gives:
u2=2gh(M+m)2m2
Step 7: Substitute known values
Substituting g=10m/s2, h=0.1m, m=0.025kg, and M=5.0kg:
u2=2×10×0.1×(5+0.025)2(0.025)2
Calculating:
=2×10×0.1×(5.025)20.000625
Step 8: Calculate u
Calculating the right-hand side:
1. (5.025)2≈25.250625
2. 2×10×0.1≈2
3. u2=2×25.2506250.000625≈80800
4. Taking the square root gives u≈√80800≈284.2m/s
Final Answer
The speed of the bullet is approximately 284.2m/s.
---
- Mass of the bullet, m=25g=0.025kg
- Mass of the pendulum, M=5.0kg
- The vertical displacement of the pendulum, h=10cm=0.1m
When the bullet embeds itself into the pendulum, we can apply the conservation of momentum:
mu=(M+m)v
Where:
- u is the initial speed of the bullet,
- v is the speed of the pendulum and bullet just after the collision.
v=mM+mu
After the collision, the kinetic energy of the bullet and pendulum system is converted into potential energy as the pendulum rises:
12(M+m)v2=(M+m)gh
Where:
- g is the acceleration due to gravity (approximately 10m/s2).
12v2=gh
Substituting v=mM+mu into the energy equation:
12(mM+mu)2=gh
This leads to:
12m2(M+m)2u2=gh
Rearranging gives:
u2=2gh(M+m)2m2
Substituting g=10m/s2, h=0.1m, m=0.025kg, and M=5.0kg:
u2=2×10×0.1×(5+0.025)2(0.025)2
Calculating:
=2×10×0.1×(5.025)20.000625
Calculating the right-hand side:
1. (5.025)2≈25.250625
2. 2×10×0.1≈2
3. u2=2×25.2506250.000625≈80800
4. Taking the square root gives u≈√80800≈284.2m/s
The speed of the bullet is approximately 284.2m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View SolutionA bullet of mass 5gm is fired horizontally into block of mass 1kg at rest on a horizontal surface and gets embedded in it. The combination moves 5m before coming to rest. If μk=0.40, what is the speed with which the bullet strikes the block ?
View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A bullet of mass 2g travelling at a speed of 500m/s is fired into a ballistic pendulum of mass 1.0kg suspended from a cord 1.0m long. The bullet penetrates the pendulum and emerges with a velocity of 100m/s. Through what vertical height will the pendulum rise?
View SolutionA bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
View SolutionA bullet of mass 50g if fired from below into the bob of mass 450g of a long simple pendulum as shown in Fig. The bullet remains inside the bob and the bob rises through a height of 1.8m. Find the speed of the bullet.Take g=10ms2
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
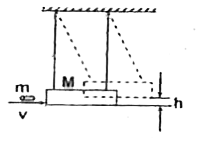
Initial speed of the bullet is
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
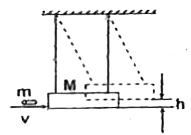
If the bullet penetrates the block to a depth of 3.0 cm, the approximate average force of resistance by the block of wood is
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
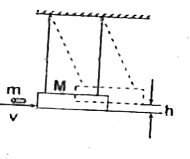
Fraction of initial energy lost in the collision
View SolutionA bullet of mass 5 g is fired at a velocity of 900ms−1 from a rifle of mass 2.5 kg. What is the recoil velocity of the rifle?
View Solution
