A chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
The correct Answer is:A, B, C
To solve the problem step by step, we need to find the gravitational potential energy of the chain, the kinetic energy when it slides down, and the tangential acceleration when it starts sliding.
Step 1: Calculate the Gravitational Potential Energy (U)
1. Understanding the Setup: The chain of length l and mass m is lying on the surface of a sphere of radius R with one end tied to the top of the sphere. The reference level for potential energy is taken at the center of the sphere.
2. Height Calculation: The height h of a small element of the chain at an angle θ from the vertical can be expressed as:
h=R−Rcos(θ)=R(1−cos(θ))
3. Mass of the Element: The mass of a small segment dθ of the chain can be expressed as:
dm=mlRdθ
4. Potential Energy of the Element: The potential energy dU of this small element is given by:
dU=dm⋅g⋅h=(mlRdθ)g⋅R(1−cos(θ))
dU=mgR2l(1−cos(θ))dθ
5. Total Potential Energy: To find the total potential energy of the chain, integrate dU from 0 to ϕ (where ϕ=lR):
U=∫ϕ0mgR2l(1−cos(θ))dθ
6. Integrating: The integral can be split:
U=mgR2l(θ−sin(θ))ϕ0
U=mgR2l(ϕ−sin(ϕ))
Step 2: Calculate the Kinetic Energy (K)
1. Change in Potential Energy: When the chain slides down through an angle θ, the change in potential energy ΔU is:
ΔU=Uinitial−Ufinal
2. Final Potential Energy: The limits of integration change to θ to θ+ϕ:
Ufinal=mgR2l(θ+ϕ−sin(θ+ϕ))
3. Kinetic Energy: Using conservation of energy, the kinetic energy K gained is equal to the loss in potential energy:
K=ΔU=Uinitial−Ufinal
Step 3: Calculate the Tangential Acceleration (a)
1. Force Calculation: The tangential force acting on the chain is given by:
F=−dUds
where ds=Rdθ.
2. Acceleration: The tangential acceleration a can be expressed as:
a=Fm
3. Final Expression: After substituting and simplifying, we find:
a=g(Rl)(1−cos(ϕ))
Summary of Results
- Gravitational Potential Energy:
U=mgR2l(ϕ−sin(ϕ))
- Kinetic Energy:
K=Uinitial−Ufinal
- Tangential Acceleration:
a=g(Rl)(1−cos(ϕ))
h=R−Rcos(θ)=R(1−cos(θ))
dm=mlRdθ
dU=dm⋅g⋅h=(mlRdθ)g⋅R(1−cos(θ))
dU=mgR2l(1−cos(θ))dθ
U=∫ϕ0mgR2l(1−cos(θ))dθ
U=mgR2l(θ−sin(θ))ϕ0
U=mgR2l(ϕ−sin(ϕ))
ΔU=Uinitial−Ufinal
Ufinal=mgR2l(θ+ϕ−sin(θ+ϕ))
K=ΔU=Uinitial−Ufinal
F=−dUds
where ds=Rdθ.
a=Fm
a=g(Rl)(1−cos(ϕ))
U=mgR2l(ϕ−sin(ϕ))
K=Uinitial−Ufinal
a=g(Rl)(1−cos(ϕ))
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 More Than One Correct
Explore 9 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
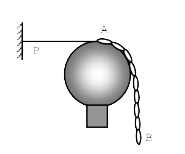
View SolutionA unifrom flexible chain of length 32 m rests on a fixed smooth sphere of radius R=2π m such that one end A of chain is on the top of the sphere while the other end B is hanging freely. Chain is helpd stationary by a horizontal thread PA as shown . Calculate the acceleration of chain when the horizontal string PA is burnt ( g = 10 m/s2)
View SolutionA chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
View SolutionA chain of length L and mass m is placed upon a smooth surface. The length of BA is (L−b). Calculate the velocity of the chain when its and reaches B

View SolutionA uniform chain of length l and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA small mass m starts from rest and slides down the surface of a frictionless solid sphere of radius R. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and the sphere, does the mass of fly off at a greater or lesser angle than the previous one ?
View Solution