A charged particle of charge 'Q' is held fixed and another charged particle of mass 'm' and charge 'q' (of the same sign) is released from a distance 'r'. The impulse of the force exerted by the external agent on the fixed charge by the time distance between 'Q' and 'q' becomes 2r is
√Qq4πε0mr
√Qqm4πε0r
√Qqmπε0r
√Qqm2πε0r
The correct Answer is:B
To solve the problem step by step, we will analyze the situation using the principles of electrostatics and mechanics.
Step 1: Understand the Problem
We have two charged particles:
- A fixed particle with charge Q.
- A movable particle with charge q and mass m that is released from a distance r from the fixed charge.
Since both charges have the same sign, they will repel each other.
Step 2: Identify the Forces Acting on the Movable Charge
When the charge q is released, it experiences a repulsive electrostatic force due to the charge Q. The force F between the two charges can be calculated using Coulomb's Law:
F=k⋅|Q⋅q|r2
where k is Coulomb's constant.
Step 3: Calculate the Initial and Final Energies
Initially, the potential energy Ui when the distance is r is given by:
Ui=k⋅Q⋅qr
The initial kinetic energy Ki is zero since the charge q is at rest.
When the distance becomes 2r, the final potential energy Uf is:
Uf=k⋅Q⋅q2r
The final kinetic energy Kf can be expressed as:
Kf=12mv2
Step 4: Apply Conservation of Energy
According to the conservation of energy:
Ui+Ki=Uf+Kf
Substituting the values:
k⋅Q⋅qr+0=k⋅Q⋅q2r+12mv2
Rearranging gives:
k⋅Q⋅qr−k⋅Q⋅q2r=12mv2
k⋅Q⋅q2r=12mv2
Multiplying both sides by 2:
k⋅Q⋅qr=mv2
Thus, solving for v:
v=√k⋅Q⋅qmr
Step 5: Calculate the Change in Momentum
The initial momentum pi is:
pi=0(since the charge is initially at rest)
The final momentum pf is:
pf=mv=m√k⋅Q⋅qmr=√mkQq
The change in momentum Δp is:
Δp=pf−pi=√mkQq−0=√mkQq
Step 6: Impulse Calculation
Impulse J is defined as the change in momentum:
J=Δp=√mkQq
Conclusion
The impulse of the force exerted by the external agent on the fixed charge by the time the distance between Q and q becomes 2r is:
J=√mkQq
We have two charged particles:
- A fixed particle with charge Q.
- A movable particle with charge q and mass m that is released from a distance r from the fixed charge.
When the charge q is released, it experiences a repulsive electrostatic force due to the charge Q. The force F between the two charges can be calculated using Coulomb's Law:
F=k⋅|Q⋅q|r2
where k is Coulomb's constant.
Initially, the potential energy Ui when the distance is r is given by:
Ui=k⋅Q⋅qr
The initial kinetic energy Ki is zero since the charge q is at rest.
Uf=k⋅Q⋅q2r
The final kinetic energy Kf can be expressed as:
Kf=12mv2
According to the conservation of energy:
Ui+Ki=Uf+Kf
Substituting the values:
k⋅Q⋅qr+0=k⋅Q⋅q2r+12mv2
Rearranging gives:
k⋅Q⋅qr−k⋅Q⋅q2r=12mv2
k⋅Q⋅q2r=12mv2
Multiplying both sides by 2:
k⋅Q⋅qr=mv2
Thus, solving for v:
v=√k⋅Q⋅qmr
The initial momentum pi is:
pi=0(since the charge is initially at rest)
The final momentum pf is:
pf=mv=m√k⋅Q⋅qmr=√mkQq
The change in momentum Δp is:
Δp=pf−pi=√mkQq−0=√mkQq
Impulse J is defined as the change in momentum:
J=Δp=√mkQq
The impulse of the force exerted by the external agent on the fixed charge by the time the distance between Q and q becomes 2r is:
J=√mkQq
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionTwo particle of equal mass m and charge q are placed at a distance of 16 cm. They do not experience any force. The value of qm is
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
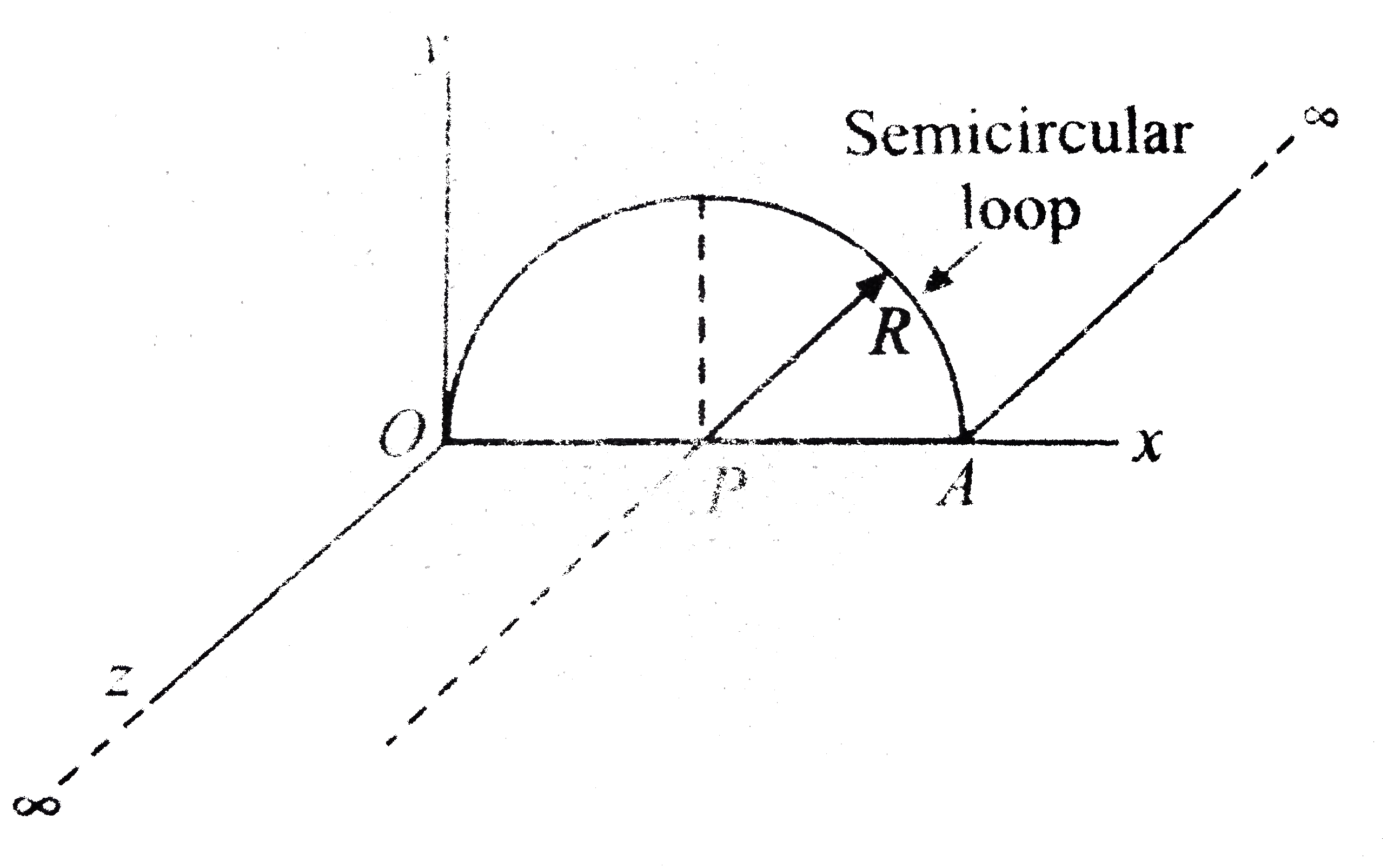
View SolutionA particle having charge + q is fixed at a point O and a second particle of mass m and having charge −q0 moves with constant speed in a circle of radius r about the charge +q. the energy required to be supplied to the moving charge to increase radius of the path to 2r is qq0nπε0r. Find the value of n.
View Solution
