A child's pogo stick(figure) stores energy in a spring with a force constant of 2.5x104Nm. At position (A) (xA=0.10m), the spring compression is a maximum and the child is momentarily at rest. At position (B) (xB=0), the spring is relaxed and the child is moving upward. At position (C), the child is again momentarily at rest at the top of the jump. The combined mass of child and pogo stick is 25kg. (a) Calculate the total energy of the child-stick-earth system if both gravitational and elastic potential energies are zero for x=0. (b) Determine xC. (c) Calculate the speed of the child at x=0. (d) Determine the value of x for which the kinetic energy of the system is a maximum. (e) Calculate the child's maximum upward speed.
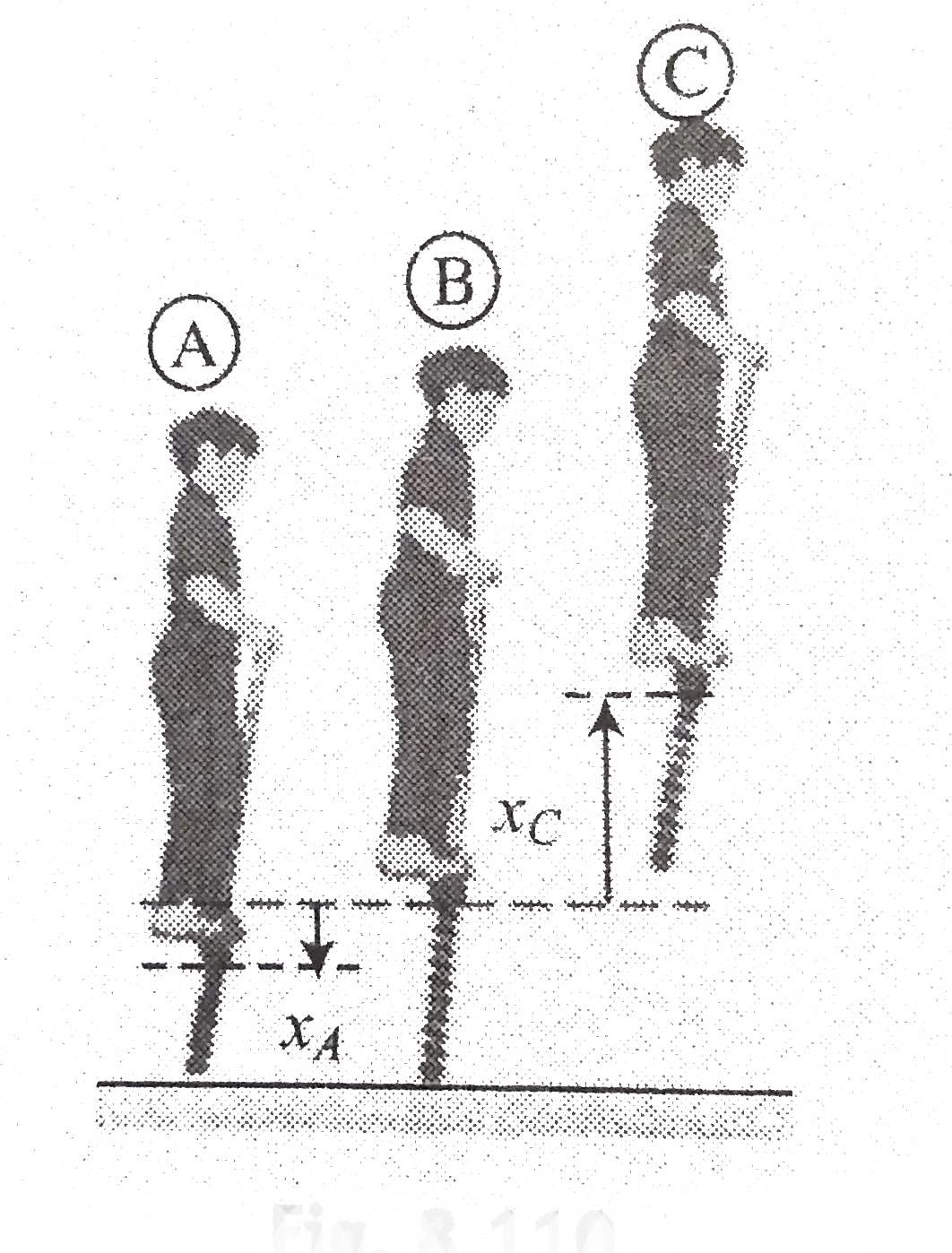
k=2.5×104Nm−1, m=25kg, XA=−0.10m,
Ug∣∣x=0=Us∣∣x=0=0
a. Emech=KA+UgA+UsA=0+mgxA+12kx2A
=25×10×(−0.100)+12×2.5×104×(−0.100)2
=−25J+125J=100J
b. Since only conservation forces are involved, the total energy of the child-pogo stick-earth system at point C is the same as that at point A.
KC+UgC+UsC=KA+UgA+UsA
0=25×10×xC+0=0−25J+125J
xC=0.40m
c. KB+UgBB+UsB=KA+UgA+UsA
12×25×v2B+0+0=0+(−25)+125
vB=2√2ms−1
d. K and v are at a maximum when a=∑F/m=0 (i.e., when the magnitude of the upward spring force equals the magnitude of the downward gravitational force).
This occurs at x<0, where k|x|=mg.
|x|=25×102.5×104=10×10−3m=10mm
Thus, K=Kmax at x=−10mm
e. 12×25×v2max=25×10×[(−0.100)−(−0.01)]+12(25×104)[(−0.100)2−(−0.01)2]
⇒vmax=2.85ms−1
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
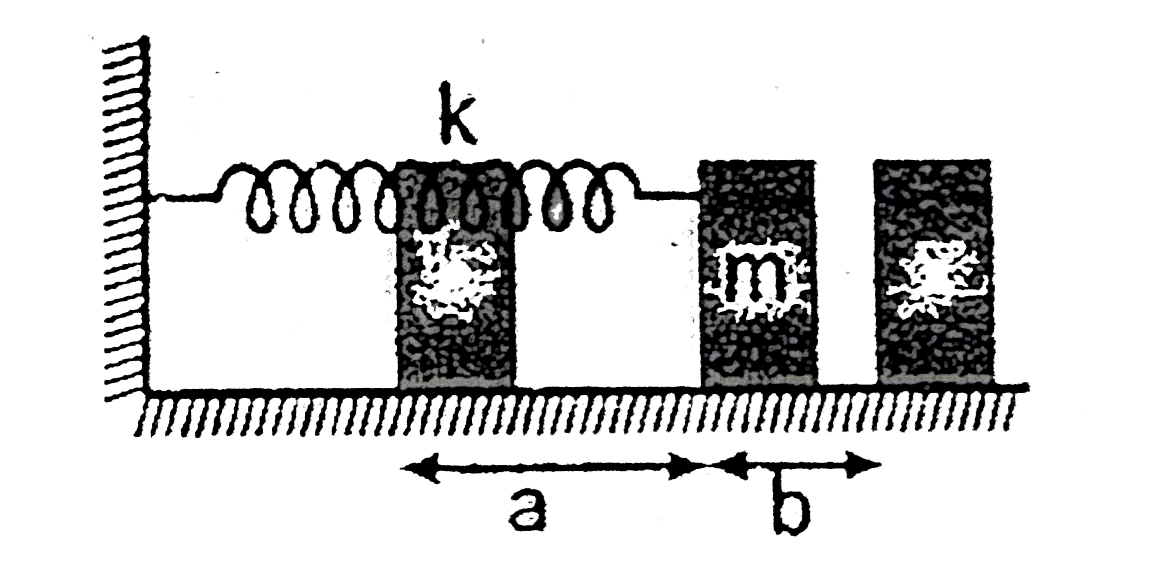
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionA colourblind child have both normal parents, the child is
View SolutionChild B is born with the characteristic palmer crease on the palm Which statement about this child is correct ?
View SolutionIf a spring extends by x on loading, then the energy stored by the spring is (if T is tension in the spring and k is spring constant)
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionAt time t , the position of a body moving along the x - axis is x=(t3−6t2+9t)m Then, it momentarily comes to rest at
View SolutionA child has near point at 10 cm. What is the maximum angular magnification the child can have with a convex lens of focal length 10 cm?
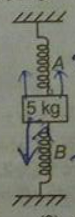
View SolutionA 5 kg block in connected with two spring A and B having force constant, K1=200Nm and K2=300Nm respectively as shown in the figure . The block is released from rest with both the springs in natural length. The maximum energy stored in the spring A will be
View Solution