A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
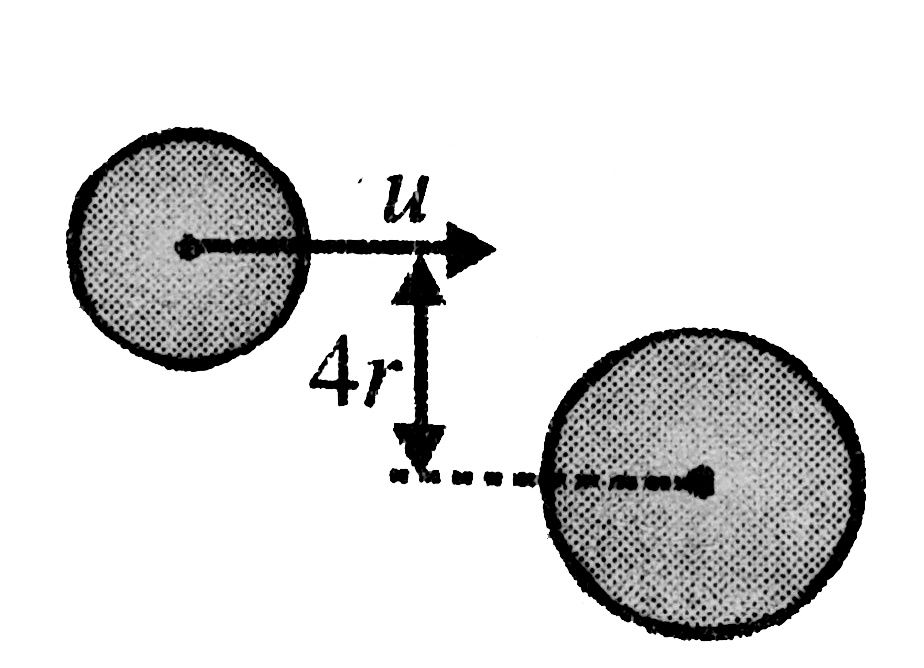 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
a. u5
b 2u5
c. 3u5
d. 4u5
The correct Answer is:B
Tangential component =usinθ=4u5
along normal velocity of m before collision:
u1=ucosθ=(3u)/5
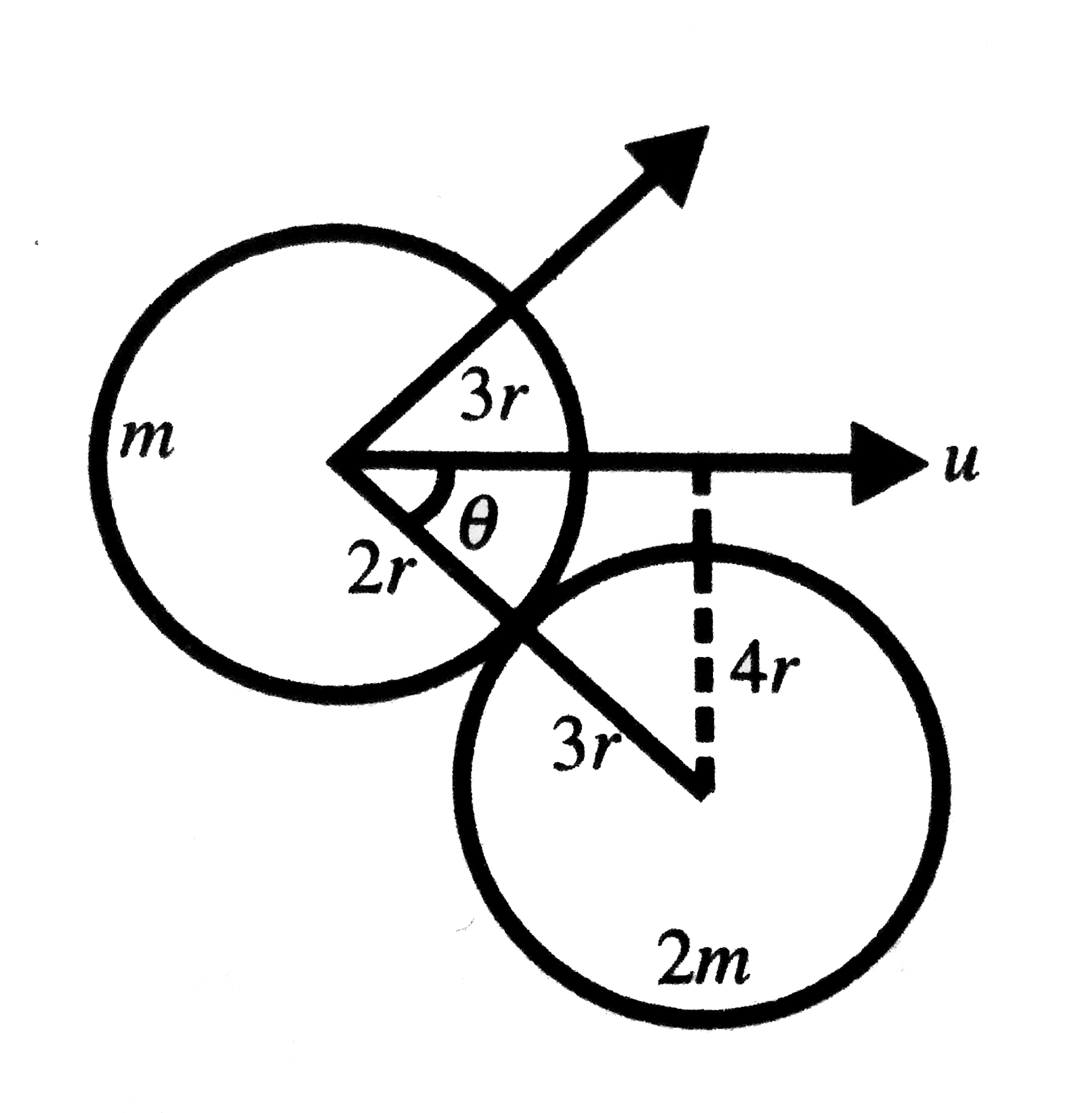
Along normal mv1+2mv2=mu1
v2−v1u1=1
solve to get v1=−u5,v2=2u5
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
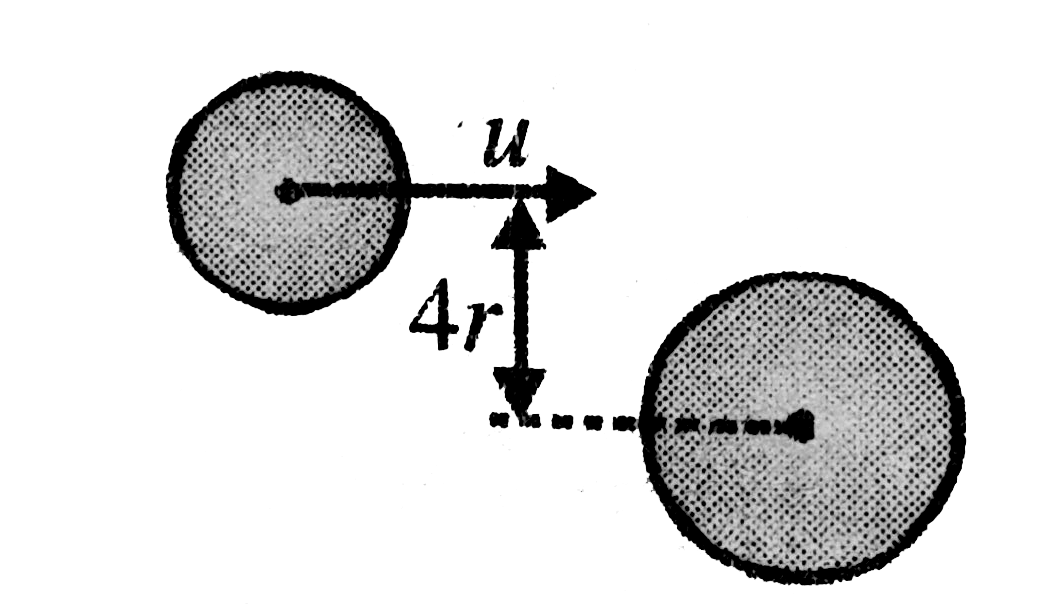
What is the tangential component of final velocity of the smaller disc?
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
What is the magnitude of normal component of final velocity of the smaller disc'?
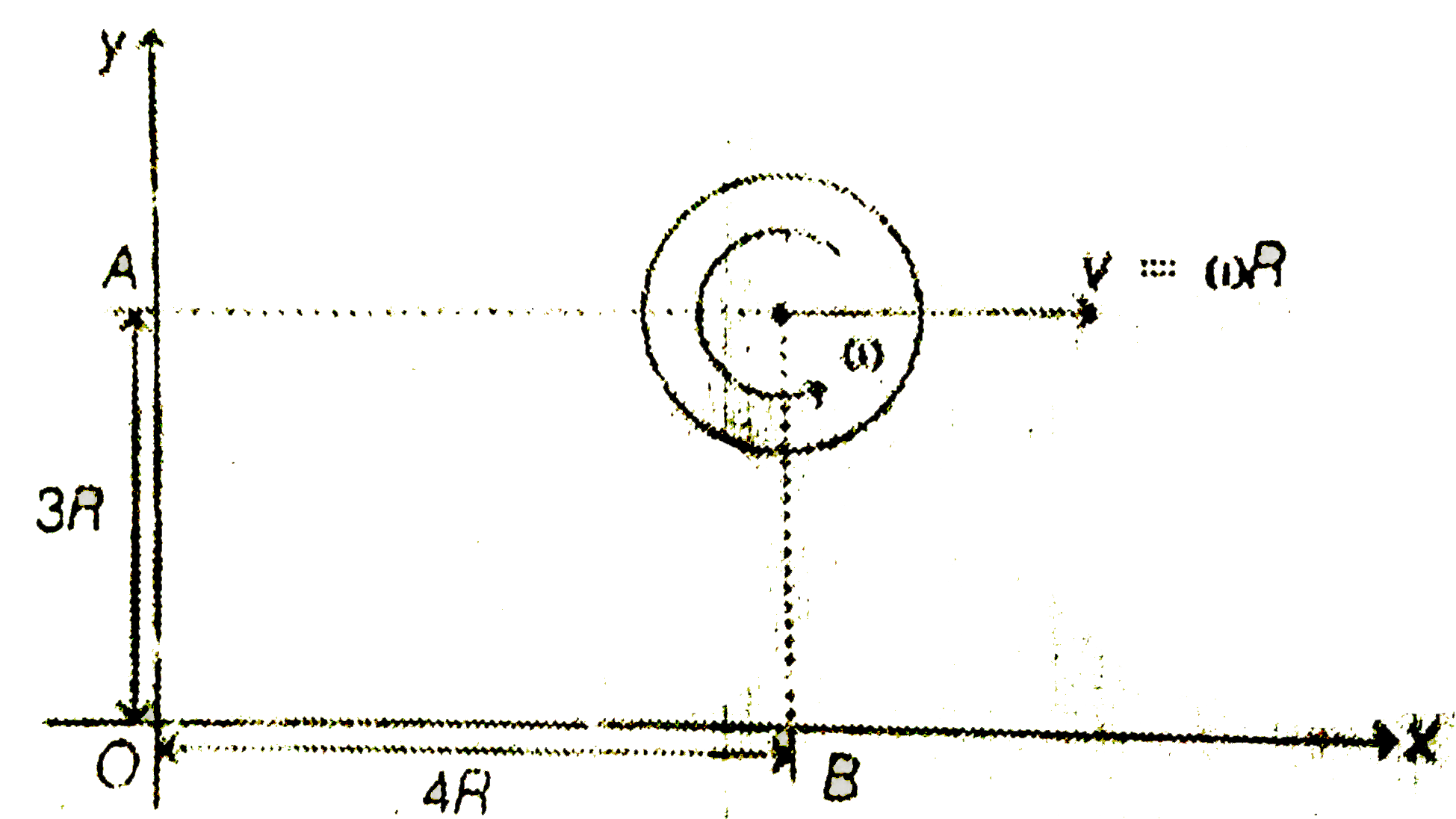
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionA small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of larger disc after collision is
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View Solution
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
View Solution
