A cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
The correct Answer is:A, C
To solve the problem of determining the minimum edge length of a cubical block of ice that can float while supporting a metal piece weighing 0.5 kg, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
The block of ice must balance the weight of the metal piece and its own weight with the buoyant force acting on it. The forces can be expressed as:
- Weight of the metal piece (W_metal) = m_metal * g
- Weight of the ice block (W_ice) = m_ice * g
- Buoyant force (F_buoyant) = ρ_water * V_submerged * g
Where:
- m_metal = 0.5 kg (weight of the metal piece)
- ρ_water = 1000 kg/m³ (density of water)
- V_submerged = volume of the submerged part of the ice block
Step 2: Relate the Mass of Ice to its Volume
The specific gravity of ice is given as 0.9, which means:
- ρ_ice = 0.9 * ρ_water = 0.9 * 1000 kg/m³ = 900 kg/m³
The volume of the ice block (V_ice) can be expressed in terms of its edge length (x):
- V_ice = x³
The mass of the ice block can then be calculated as:
- m_ice = ρ_ice * V_ice = 900 kg/m³ * x³
Step 3: Set Up the Equation for Equilibrium
The total weight supported by the buoyant force can be expressed as:
- F_buoyant = W_ice + W_metal
Substituting the expressions for weight:
- ρ_water * V_submerged * g = (900 kg/m³ * x³ * g) + (0.5 kg * g)
Since g cancels out from both sides, we have:
- 1000 kg/m³ * V_submerged = 900 kg/m³ * x³ + 0.5 kg
Step 4: Determine the Volume Submerged
For a floating block, the volume submerged (V_submerged) is equal to the volume of the ice block:
- V_submerged = x³
Substituting this into the equation gives:
- 1000 kg/m³ * x³ = 900 kg/m³ * x³ + 0.5 kg
Step 5: Rearranging the Equation
Rearranging the equation to isolate x³:
- 1000 x³ - 900 x³ = 0.5
- 100 x³ = 0.5
- x³ = 0.5 / 100
- x³ = 0.005 m³
Step 6: Calculate the Edge Length
To find the edge length x, take the cube root:
- x = (0.005)^(1/3)
Calculating this gives:
- x ≈ 0.17 m or 17 cm
Conclusion
The minimum edge length of the block of ice that can float while supporting the metal piece is approximately 17 cm.
---
The block of ice must balance the weight of the metal piece and its own weight with the buoyant force acting on it. The forces can be expressed as:
- Weight of the metal piece (W_metal) = m_metal * g
- Weight of the ice block (W_ice) = m_ice * g
- Buoyant force (F_buoyant) = ρ_water * V_submerged * g
- m_metal = 0.5 kg (weight of the metal piece)
- ρ_water = 1000 kg/m³ (density of water)
- V_submerged = volume of the submerged part of the ice block
The specific gravity of ice is given as 0.9, which means:
- ρ_ice = 0.9 * ρ_water = 0.9 * 1000 kg/m³ = 900 kg/m³
- V_ice = x³
- m_ice = ρ_ice * V_ice = 900 kg/m³ * x³
The total weight supported by the buoyant force can be expressed as:
- F_buoyant = W_ice + W_metal
- ρ_water * V_submerged * g = (900 kg/m³ * x³ * g) + (0.5 kg * g)
- 1000 kg/m³ * V_submerged = 900 kg/m³ * x³ + 0.5 kg
For a floating block, the volume submerged (V_submerged) is equal to the volume of the ice block:
- V_submerged = x³
- 1000 kg/m³ * x³ = 900 kg/m³ * x³ + 0.5 kg
Rearranging the equation to isolate x³:
- 1000 x³ - 900 x³ = 0.5
- 100 x³ = 0.5
- x³ = 0.5 / 100
- x³ = 0.005 m³
To find the edge length x, take the cube root:
- x = (0.005)^(1/3)
- x ≈ 0.17 m or 17 cm
The minimum edge length of the block of ice that can float while supporting the metal piece is approximately 17 cm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question2videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct36videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Single Correct49videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water? specific gravity of ice=0.9.
View SolutionA cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron =8000kgm−3and density of water =1000kgm−3.
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View SolutionA cubical block of side 0.5 M floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take density of water =103kg/m3]View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA metal ball of specific gravity 4.5 and specific heat 0.1cal/gm−∘C is placed on a large slab of ice at 0∘C. Half of the ball sinks in the ice. The initial temperature of the ball is:- (Latent heat capacity of ice =80cal/g, specific gravity of ice =0.9)
View SolutionA block of ice of total area A and thicknes 0.5m is floating in water. In order to just support a man of nass 100kg, the area A should be (the specific gravity of ice is 0.9)
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
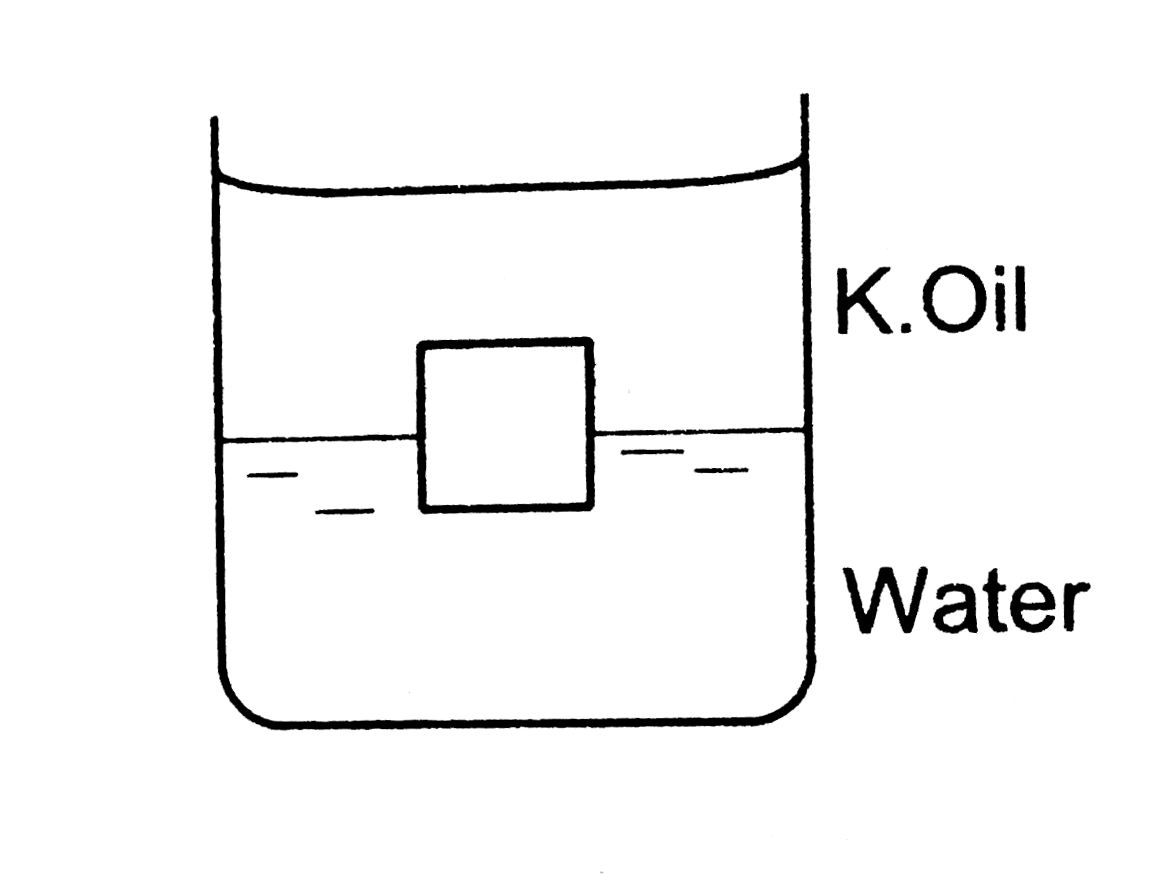 View Solution
View SolutionThe ratio of masses of a cubical block of wood and a chunk of concrete is 3/5 so that the combination just floats with entire volume submerged under water. If the specific gravity of wood is 0.5 then specific gravity of concrete will be
View SolutionA block of ice is floating in a liquid of specific gravity 1.2 contained in the beaker. What will be the effect on the level of liquid in the beaker when the whole ice melts?
View Solution

