A current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
1/r2
1/r
1/r3
1/√r
The correct Answer is:B
To solve the problem of finding the magnetic induction B at a point due to an infinitely long straight conductor carrying a current I, we can use the principles of magnetism, specifically the Biot-Savart Law. Here’s a step-by-step solution:
Step 1: Understanding the Setup
We have an infinitely long straight conductor carrying a current I. We want to find the magnetic field B at a point P which is at a perpendicular distance r from the lower end of the conductor.
Hint: Visualize the scenario with the conductor and the point P to understand the geometry involved.
Step 2: Applying Biot-Savart Law
According to the Biot-Savart Law, the magnetic field B at a distance r from a straight conductor carrying a current I can be expressed as:
B=μ0I4π∫dLsinθr2
where dL is an infinitesimal length of the conductor, θ is the angle between the current element and the line connecting the element to the point P, and r is the distance from the current element to the point.
Hint: Remember that for an infinitely long straight wire, the angles α and β will simplify the calculation.
Step 3: Analyzing Angles
In our case:
- The angle α (angle from the upper end) is 90∘.
- The angle β (angle from the lower end) is 0∘.
Thus, we have:
sin(90∘)=1andsin(0∘)=0
Hint: Use the sine values to simplify the expression for B.
Step 4: Simplifying the Expression
Substituting the sine values into the Biot-Savart Law, we get:
B=μ0I4π⋅1r⋅1
This leads to:
B=μ0I4πr
Hint: Focus on the relationship between B and r to identify the proportionality.
Step 5: Conclusion
From the expression B=μ0I4πr, we can see that the magnetic induction B is inversely proportional to the distance r:
B∝1r
Thus, the correct option is that the magnetic induction B is inversely proportional to r.
Final Answer: The magnetic induction B is inversely proportional to r (Option 2).
We have an infinitely long straight conductor carrying a current I. We want to find the magnetic field B at a point P which is at a perpendicular distance r from the lower end of the conductor.
According to the Biot-Savart Law, the magnetic field B at a distance r from a straight conductor carrying a current I can be expressed as:
B=μ0I4π∫dLsinθr2
where dL is an infinitesimal length of the conductor, θ is the angle between the current element and the line connecting the element to the point P, and r is the distance from the current element to the point.
In our case:
- The angle α (angle from the upper end) is 90∘.
- The angle β (angle from the lower end) is 0∘.
sin(90∘)=1andsin(0∘)=0
Substituting the sine values into the Biot-Savart Law, we get:
B=μ0I4π⋅1r⋅1
This leads to:
B=μ0I4πr
From the expression B=μ0I4πr, we can see that the magnetic induction B is inversely proportional to the distance r:
B∝1r
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together75videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason20videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
Similar Questions
A current I ampere flows along an infinitely long straight thin walled tube, then the magnetic induction at any point inside the tube is .
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionIn the diagram shown, I1,I2 are the magnitudes of current in the squre loop and infinite long straight conductor respectively. If the net magnetic field at the centre of the loop is zero, then the relation between I1andI2 is
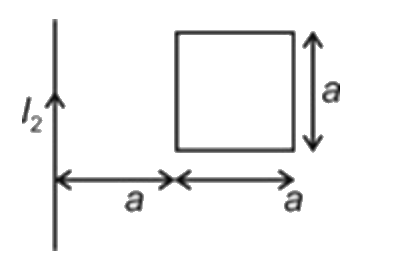 View Solution
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View SolutionTwo long straight conductors with current I1 and I2 are placed along X and Y axes. The equation of locus of points of zero magnetic induction is :
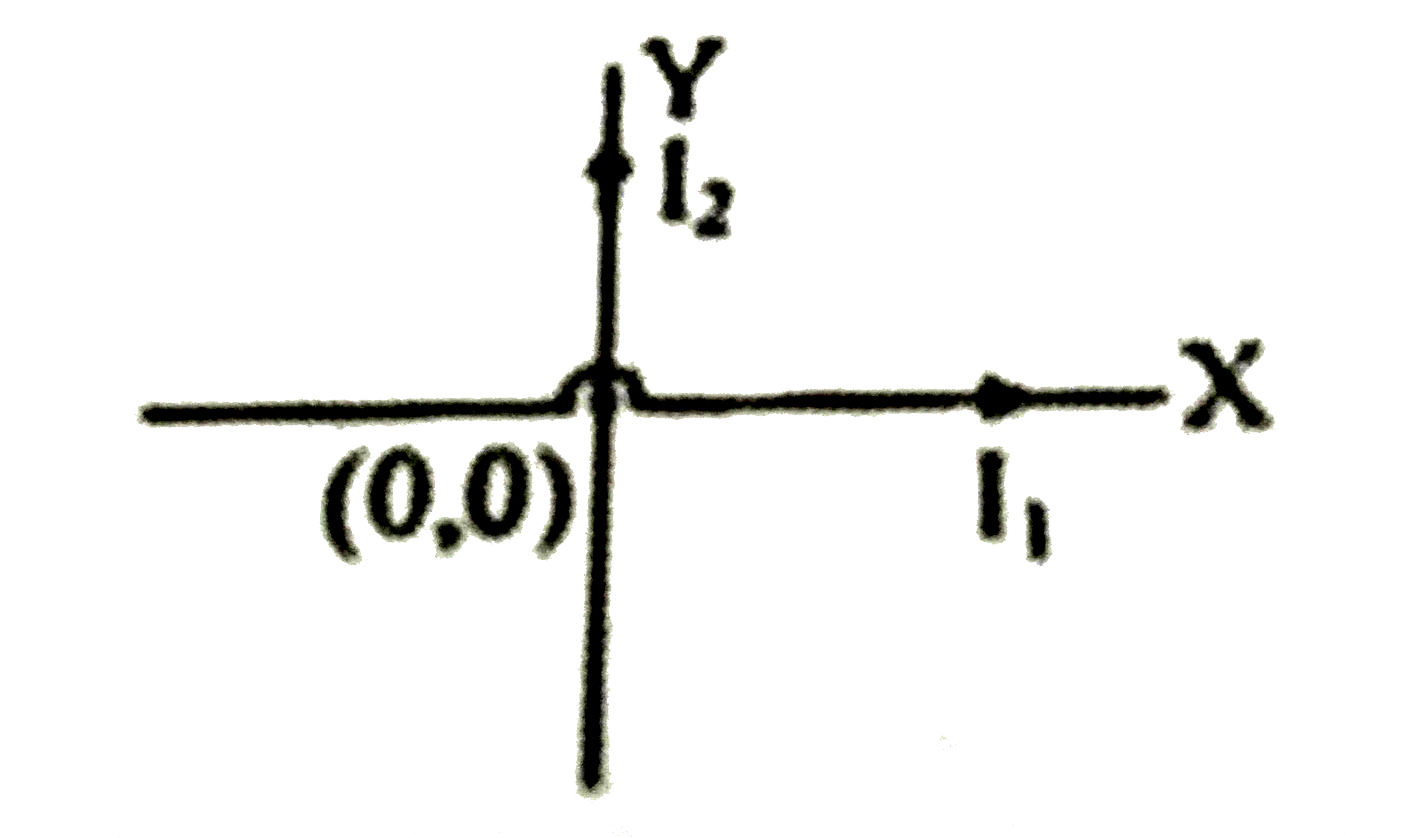 View Solution
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionThe strength of magnetic field around an infinitely long current carrying conductor is
View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionA current I is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be
View Solution

