A current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
To show that the net magnetic force acting on a current loop of arbitrary shape in a uniform magnetic field B is zero, we can follow these steps:
Step 1: Understand the Magnetic Force on a Current Loop
The magnetic force F acting on a current-carrying conductor in a magnetic field can be expressed as:
F=IL×B
where:
- I is the current flowing through the loop,
- L is the length vector of the conductor segment,
- B is the magnetic field vector.
Step 2: Consider the Current Loop
Let’s consider a current loop of arbitrary shape placed in a uniform magnetic field B. The loop consists of multiple small segments, each carrying the current I.
Step 3: Analyze Each Segment of the Loop
For each infinitesimal segment dL of the loop, the magnetic force can be expressed as:
dF=IdL×B
The total magnetic force on the entire loop can be found by integrating over the entire loop:
F=∫dF=I∫(dL×B)
Step 4: Use the Properties of the Loop
Since the loop is closed, the integral of the displacement vector dL over the entire loop is zero:
∮dL=0
This means that for every segment of the loop contributing to the force, there is an equal and opposite segment that cancels it out.
Step 5: Conclude that the Net Force is Zero
Thus, when we evaluate the total magnetic force on the loop:
F=I∮(dL×B)=0
This shows that the net magnetic force acting on the current loop in a uniform magnetic field is zero.
Final Statement
Therefore, we conclude that the net magnetic force acting on a current loop of arbitrary shape in a uniform magnetic field B is indeed zero.
---
The magnetic force F acting on a current-carrying conductor in a magnetic field can be expressed as:
F=IL×B
where:
- I is the current flowing through the loop,
- L is the length vector of the conductor segment,
- B is the magnetic field vector.
Let’s consider a current loop of arbitrary shape placed in a uniform magnetic field B. The loop consists of multiple small segments, each carrying the current I.
For each infinitesimal segment dL of the loop, the magnetic force can be expressed as:
dF=IdL×B
The total magnetic force on the entire loop can be found by integrating over the entire loop:
F=∫dF=I∫(dL×B)
Since the loop is closed, the integral of the displacement vector dL over the entire loop is zero:
∮dL=0
This means that for every segment of the loop contributing to the force, there is an equal and opposite segment that cancels it out.
Thus, when we evaluate the total magnetic force on the loop:
F=I∮(dL×B)=0
This shows that the net magnetic force acting on the current loop in a uniform magnetic field is zero.
Therefore, we conclude that the net magnetic force acting on a current loop of arbitrary shape in a uniform magnetic field B is indeed zero.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
A non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
View SolutionA current loop in a magnetic field
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionDerive the expression for the torque τ acting on a rectangular current loop of area A placed in a uniform magnetic field B. Show that →τ=→m×→B where →m is the moment of the current loop given by →m=→IA.
View SolutionIs it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
View Solution(a) Write the expression for the force, →F, acting on a charged particle of charge 'q', moving with a velocity →V in the presence of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by
→τ=→m×→B, where →m is the magnetic moment of the loop.View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
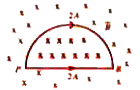 View Solution
View SolutionTwo current carrying closed loops having equal perimeters are placed in a uniform magnetic field as. Shown in the figure. What is the ratio of magnitude of torque acting on the loop [loop I is equilateral triangle and loop II is square]
 View Solution
View SolutionA square loop of side l iskept in a uniform magnetic field B such that its plane makes an angle α with →B. The loop carries a current i. The torque experienced by the loop in this position is
View SolutionStatement 1: The net force on a closed circular current carrying loop placed in a uniform magnetic field is zero.
Statement 2: The torque produced in a conducting circular ring is zero when it is placed in a uniform magnetic field such that the magnetic field is perpendicular to the plane of loop.View Solution

