A current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
To solve the problem of finding the magnetic field →B at the point (1m, 0, 0) due to a long straight wire carrying a current of 10A along the positive z-axis, we can follow these steps:
Step 1: Identify the parameters
- Current I=10A
- The position of the point where we want to find the magnetic field is given as (1m,0,0).
- The wire is along the positive z-axis.
Step 2: Calculate the distance d
The distance d from the wire (which is along the z-axis) to the point (1m, 0, 0) can be calculated using the coordinates:
- The point (1, 0, 0) is 1 meter away from the z-axis (where the wire is located).
- Therefore, d=1m.
Step 3: Use the formula for the magnetic field
The formula for the magnetic field →B at a distance d from a long straight wire carrying a current I is given by:
B=μ0I2πd
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Step 4: Substitute the values into the formula
Substituting the values into the formula:
B=(4π×10−7)⋅102π⋅1
This simplifies to:
B=4×10−7⋅102
B=2×10−6T
Step 5: Determine the direction of the magnetic field
Using the right-hand rule:
- Point your thumb in the direction of the current (positive z-axis).
- The fingers curl in the direction of the magnetic field.
- At the point (1, 0, 0), the magnetic field will be directed into the page (negative y-direction).
Thus, we can express the magnetic field vector as:
→B=−2×10−6^jT
Final Answer
The magnetic field →B at the point (1m, 0, 0) is:
→B=−2×10−6^jT
---
- Current I=10A
- The position of the point where we want to find the magnetic field is given as (1m,0,0).
- The wire is along the positive z-axis.
The distance d from the wire (which is along the z-axis) to the point (1m, 0, 0) can be calculated using the coordinates:
- The point (1, 0, 0) is 1 meter away from the z-axis (where the wire is located).
- Therefore, d=1m.
The formula for the magnetic field →B at a distance d from a long straight wire carrying a current I is given by:
B=μ0I2πd
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Substituting the values into the formula:
B=(4π×10−7)⋅102π⋅1
This simplifies to:
B=4×10−7⋅102
B=2×10−6T
Using the right-hand rule:
- Point your thumb in the direction of the current (positive z-axis).
- The fingers curl in the direction of the magnetic field.
- At the point (1, 0, 0), the magnetic field will be directed into the page (negative y-direction).
→B=−2×10−6^jT
The magnetic field →B at the point (1m, 0, 0) is:
→B=−2×10−6^jT
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Objective 2
Explore 7 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:MAGNETIC PROPERTIES OF MATTERExercise:Short Answer
Explore 6 Videos
Similar Questions
Equal currents are flowing in three infinitely long wires along positive x,y and z -directions. The magnetic field at a point (0,0−a) would be (i=current in each wire)
View SolutionSame current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
View Solution
Knowledge Check
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44N
Two long, straight wires, each carrying a current of 5A, are placed along the x and y axes respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1m, 1m), (b) (-1m, 1m), (c) (-1m, -1m) and (d) (1m, -1m).
View SolutionA current of 10.0 nA is established in a circular loop of radius 5.0 cm. find the magnetic dipole moment of the current loop. : The magnetic dipole moment is →μ=→iA.
View Solution(a). Find the magnetic field B at point O (centre) of
(i). ABCD, which is a square of side l.
(ii). ABC, which is an equilateral triangle of side l.
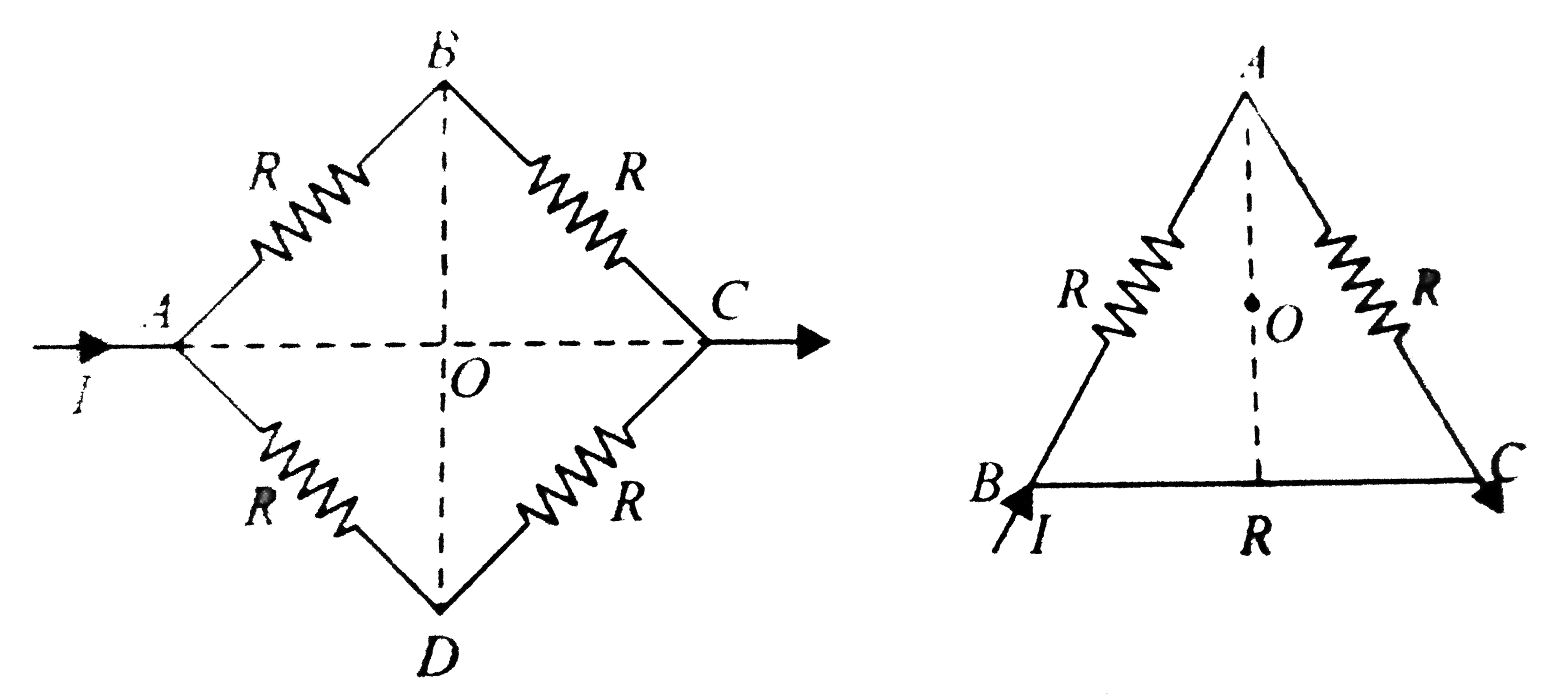
(b) Twelve uniform wires of equal length l and each of resistance r are connected to form a skelton cube. A battary of emf E is connected between two diagonally opposite corners of the cube. The magnetic induction at the centreof the cube is .........
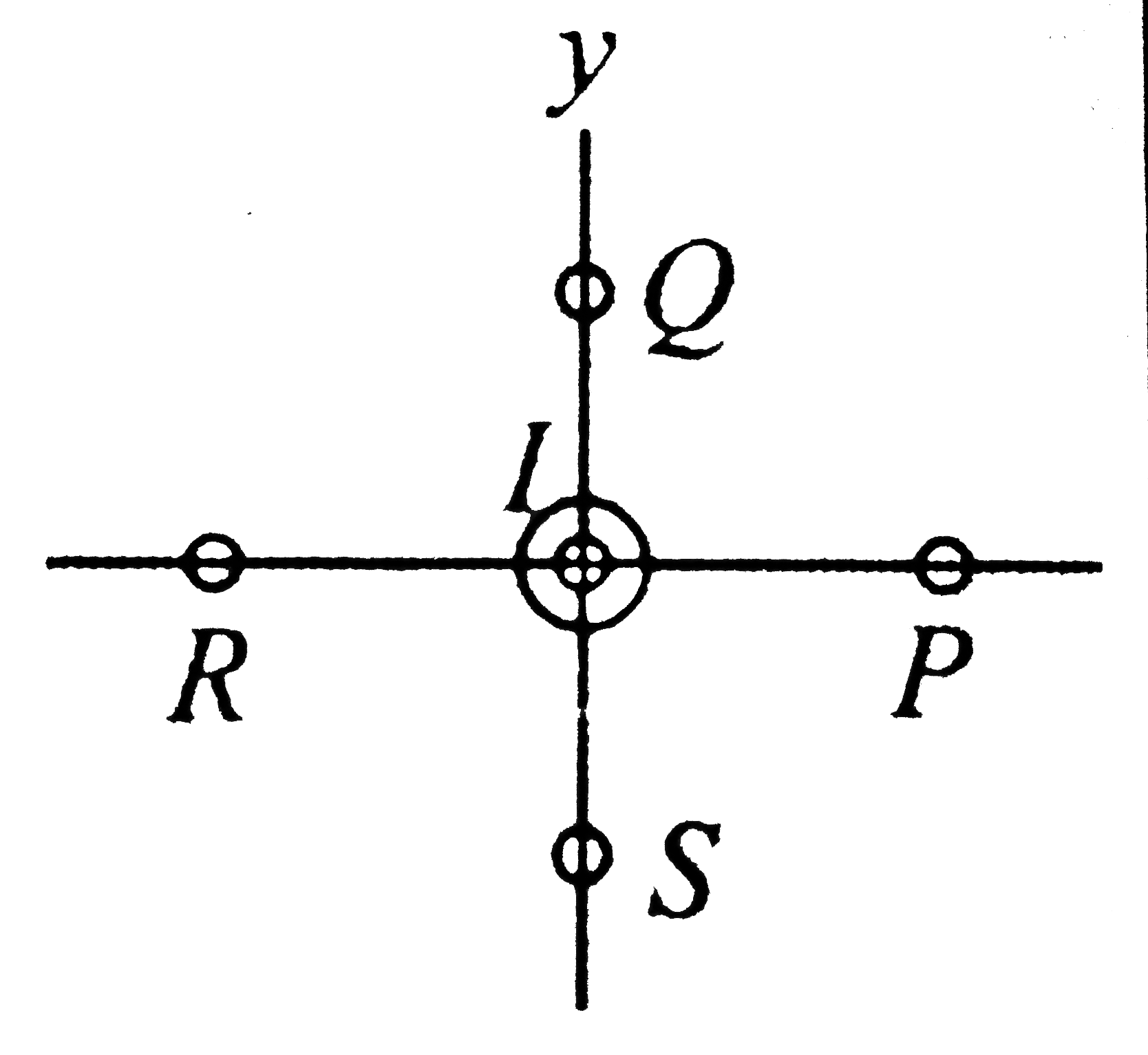
(c) An infinately long straight wire is placed at the origin along the z-axis. The current I flows along the positive z-axis. Find the unit vecotrs showing the direction of magnetic field at the four points: P(a,0),Q(0,b),R(a,0)andS(0,−b)

View SolutionA 3⋅0cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0⋅27T. What is the magnetic force on the wire?
View SolutionA charge of2.0μC moves with a speed of 2.0X106ms−1 along the positive x-axis. A magnetic field →B of strength (0.20→J+0.40→k)T exists in space. Find the magnetic force acting on the charge
View SolutionFigure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10A along opposite directions. Find the magnitude of the magnetic field B at the points A1,A2,A3andA4.

View SolutionA particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
View Solution