A cyclist is moving on a smooth horizontal curved path of radius of curvature 10m.with a speed 10 . Then his angle of leaning is
A)
B)
C)
D)
The correct Answer is:C
To find the angle of leaning of the cyclist moving on a curved path, we can use the formula for the angle of leaning, which is given by:
θ=tan−1(v2rg)
Where:
- θ is the angle of leaning,
- v is the speed of the cyclist,
- r is the radius of curvature,
- g is the acceleration due to gravity (approximately 9.8m/s2, but we can use 10m/s2 for simplicity).
1. Identify the given values:
- Speed of the cyclist, v=10m/s
- Radius of curvature, r=10m
- Acceleration due to gravity, g≈10m/s2
2. Substitute the values into the formula:
θ=tan−1(v2rg)=tan−1(10210⋅10)
3. Calculate v2:
v2=102=100
4. Calculate rg:
rg=10⋅10=100
5. Substitute these values back into the equation:
θ=tan−1(100100)=tan−1(1)
6. Find the angle whose tangent is 1:
θ=45∘
Final Answer:
The angle of leaning of the cyclist is 45∘.
---
- θ is the angle of leaning,
- v is the speed of the cyclist,
- r is the radius of curvature,
- g is the acceleration due to gravity (approximately 9.8m/s2, but we can use 10m/s2 for simplicity).
- Speed of the cyclist, v=10m/s
- Radius of curvature, r=10m
- Acceleration due to gravity, g≈10m/s2
θ=tan−1(v2rg)=tan−1(10210⋅10)
v2=102=100
rg=10⋅10=100
θ=tan−1(100100)=tan−1(1)
θ=45∘
The angle of leaning of the cyclist is 45∘.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A motorcyclist is moving in a circular path of radius 10m and with uniform speed 36kmh−1. The angle with vertical at which motorcyclist will bend is
View SolutionA cyclist moves around a circular path of radius 39.2√3 metre with a speed of 19.6ms−1 '. He must lean inwards at an angle θ with the vertical such that tanθ is
View Solution
Knowledge Check
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5ms−1 and the speed is increasing at a rate of 2ms−2. At this instant, the magnitude of the net acceleration will be
A5ms−2B2ms−2C3.2ms−2D4.3ms−2
A particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
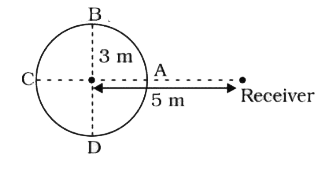
View SolutionA sonic source of requency n0=272Hz is moving along a horizontal circle of radius R=3m with a speed u=10ms−1. A stationary receiver lies in the same plane at distance d=5m from centre of the circle. Speed of sound in air is v=330ms−1.
View SolutionA car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
View SolutionA mark on the rim of a rotating cicular wheel of 0.50 m radius is moving with a speed of 10ms−1 . Find its angular speed.
View SolutionSpeed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionInside a horizontal moving box, an experimenter finds that when an object is placed on a smooth horizontal table and is released, it moves with an acceleration of 10ms−2, in this box. If 1-kg body is suspended with a light string. The tension in the string in equilibrium position. (w.r.t. experimenter) will be (take g=10ms−2)
View Solution
