A mark on the rim of a rotating cicular wheel of 0.50 m radius is moving with a speed of 10ms−1 . Find its angular speed.
The correct Answer is:20rads−1
To find the angular speed of a mark on the rim of a rotating circular wheel, we can use the relationship between linear speed (v) and angular speed (ω). The formula that relates these two quantities is:
v=ω×r
Where:
- v is the linear speed,
- ω is the angular speed,
- r is the radius of the circular wheel.
1. Identify the given values:
- Radius of the wheel, r=0.50m
- Linear speed, v=10m/s
2. Use the formula to find angular speed:
We rearrange the formula to solve for angular speed ω:
ω=vr
3. Substitute the values into the formula:
ω=10m/s0.50m
4. Calculate the angular speed:
ω=100.50=20rad/s
5. Conclusion:
The angular speed of the mark on the rim of the rotating wheel is 20rad/s.
- v is the linear speed,
- ω is the angular speed,
- r is the radius of the circular wheel.
- Radius of the wheel, r=0.50m
- Linear speed, v=10m/s
We rearrange the formula to solve for angular speed ω:
ω=vr
ω=10m/s0.50m
ω=100.50=20rad/s
The angular speed of the mark on the rim of the rotating wheel is 20rad/s.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -B Objective (one option is correct)
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Video
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Knowledge Check
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5ms−1 and the speed is increasing at a rate of 2ms−2. At this instant, the magnitude of the net acceleration will be
A5ms−2B2ms−2C3.2ms−2D4.3ms−2
Find the de Broglie wavelength of electrons moving with a speed of 7×106ms−1
View SolutionSpeed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
View SolutionA particle is moving on a circular track of radius 30 cm with a constant speed of 6ms−1. Its acceleration is
View SolutionA cyclist is moving on a smooth horizontal curved path of radius of curvature 10m.with a speed 10 ms−1. Then his angle of leaning is
View SolutionThe driver of a car moving towards a rocket launching with a speed of 6 ms−1 observed that the rocket is moving with speed of 10 ms−1 The upward speed of the rocket as seen by the stationary observer is nearly
View Solution
Particle P shown in figure is moving in a circle of radius R=10 cm with linear speed v=2m/s Find the angular speed of particle about point O.
View SolutionA sonic source of requency n0=272Hz is moving along a horizontal circle of radius R=3m with a speed u=10ms−1. A stationary receiver lies in the same plane at distance d=5m from centre of the circle. Speed of sound in air is v=330ms−1.
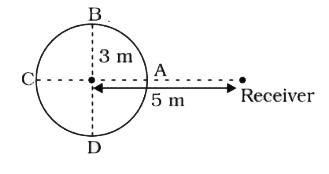
View Solution