A cylindrical capacitor has two co-axial cylinders of length 15 cm and radial 1.5 and 1.4 cm.The outer cylinder is earthed and inner cylinder is given a charge of 3.5μC. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i.e., bending of field lines at the ends.)
To solve the problem of finding the capacitance of a cylindrical capacitor and the potential of the inner cylinder, we will follow these steps:
Step 1: Identify the given values
- Length of the cylinders, l=15cm=15×10−2m
- Radius of the inner cylinder, ra=1.4cm=1.4×10−2m
- Radius of the outer cylinder, rb=1.5cm=1.5×10−2m
- Charge on the inner cylinder, Q=3.5μC=3.5×10−6C
Step 2: Use the formula for capacitance of a cylindrical capacitor
The formula for the capacitance C of a cylindrical capacitor is given by:
C=2πϵ0lln(rbra)
where ϵ0=8.85×10−12F/m (the permittivity of free space).
Step 3: Calculate the logarithm term
Calculate ln(rbra):
rbra=1.5×10−21.4×10−2=1.51.4≈1.0714
Now calculate ln(1.0714):
ln(1.0714)≈0.0686
Step 4: Substitute values into the capacitance formula
Now substitute the values into the capacitance formula:
C=2π(8.85×10−12)(15×10−2)0.0686
Calculating the numerator:
2π(8.85×10−12)(15×10−2)≈8.34×10−12F
Now divide by 0.0686:
C≈8.34×10−120.0686≈1.22×10−10F
Step 5: Calculate the potential of the inner cylinder
The potential V of the inner cylinder can be calculated using the formula:
V=QC
Substituting the values:
V=3.5×10−61.22×10−10≈2.87×104V
Final Results
- Capacitance C≈1.22×10−10F
- Potential V≈2.87×104V
---
- Length of the cylinders, l=15cm=15×10−2m
- Radius of the inner cylinder, ra=1.4cm=1.4×10−2m
- Radius of the outer cylinder, rb=1.5cm=1.5×10−2m
- Charge on the inner cylinder, Q=3.5μC=3.5×10−6C
The formula for the capacitance C of a cylindrical capacitor is given by:
Calculate ln(rbra):
Now substitute the values into the capacitance formula:
The potential V of the inner cylinder can be calculated using the formula:
- Capacitance C≈1.22×10−10F
- Potential V≈2.87×104V
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise37videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise25videos
MAGNETISM AND MATTER
Similar Questions
A cylindrical capacitor has has two co-axial cylinders of length 20 cm and radii 2r and r, inner cylinder is gliven a charge 10 μC and and outer cylinder a charge of - 10 μC. the potential difference between the two cylinders will be
View SolutionA sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical capacitor has two co-axial cylinders of length 20 cm and radii 1.5 cm and 1.6 cm. The outer cylinder is earthed and inner cylinder is given a charge 4μC. The capacitance of the system is (neglect end effect)
A2.8×10−8FB4.2×10−14FC1.7×10−10FD3.4×10−12F - Question 2 - Select One
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is p. The resistance of . the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρl
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?View SolutionA cylindrical capacitor is constructed using two coaxial cylinders of the same length 10cm of radii 2mm and 4mm. (a) calculate the capacitance (b) another capacitor of the same length is constructed with cylinders of radii 4mm and 8mm. Calculate the capacitance .
View SolutionA spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.View SolutionAn infinite line charge is at the axis of a cylinder of length 1 m and radius 7 cm. If electric field at any point on the curved surface of cylinder is 250 NC−1, then net electric flux through the cylinder is
View SolutionFigure shows two large cylindrical shells having uniform linera charge densities +λ and −λ. Radius of inner cylinder is 'a' and that of outer cylinder is 'b'. A charged particle of mass m, charge q revolves in a circle of radius r. Then, its speed 'v' is : (Neglect gravity and assume the radii of both the cylinders to be very small in comparison to their length.)
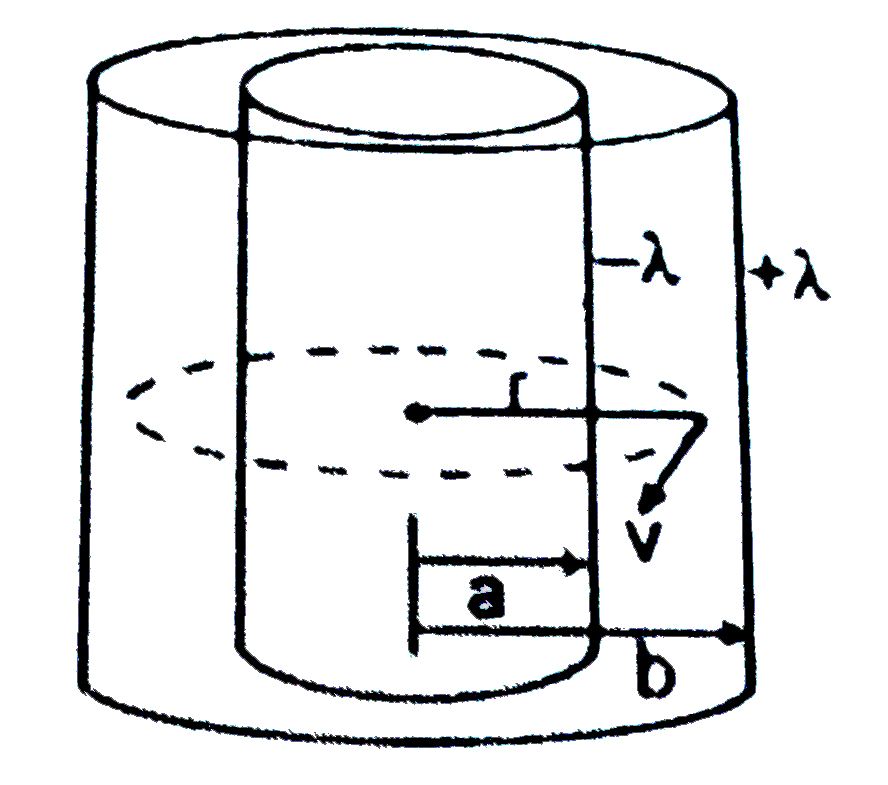 View Solution
View SolutionThe outer cylinders of two cylindrical capacitors of capacitance 2.2 microFarad each , are kept in contact and the inner cylinders are connected through a wire .A battery of end 10V is connected as shown in figure. Find the totatl charge supplied by the bettery to the inner cylioders.
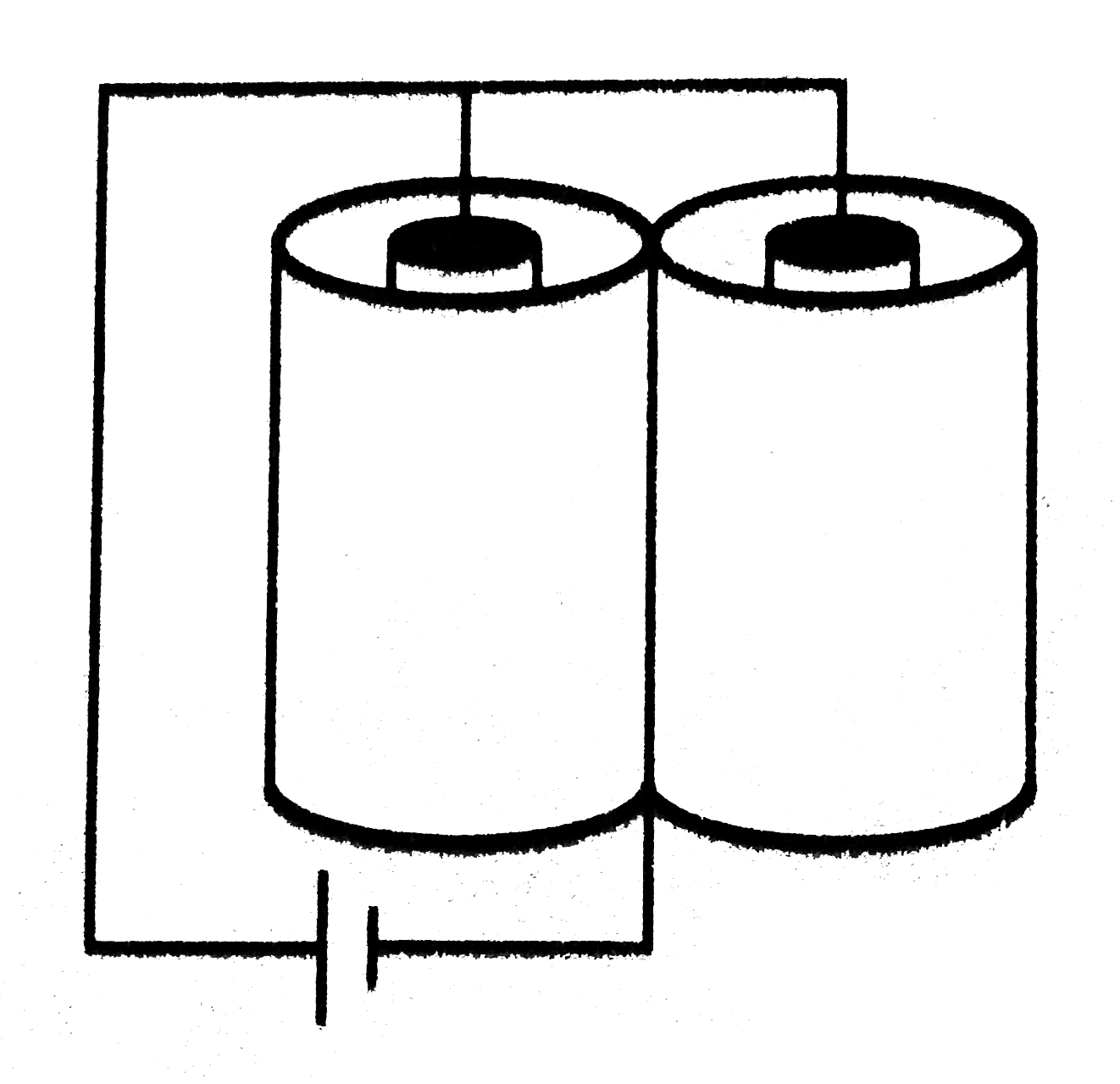 View Solution
View Solution

