A heavy particle is suspended by a stirng of length l. The particle is given a horizontal velocity v0. The stirng becomes slack at some angle and the particle proceeds on a parabola.find the value of v0 if the prticle psses through the ponit of suspension
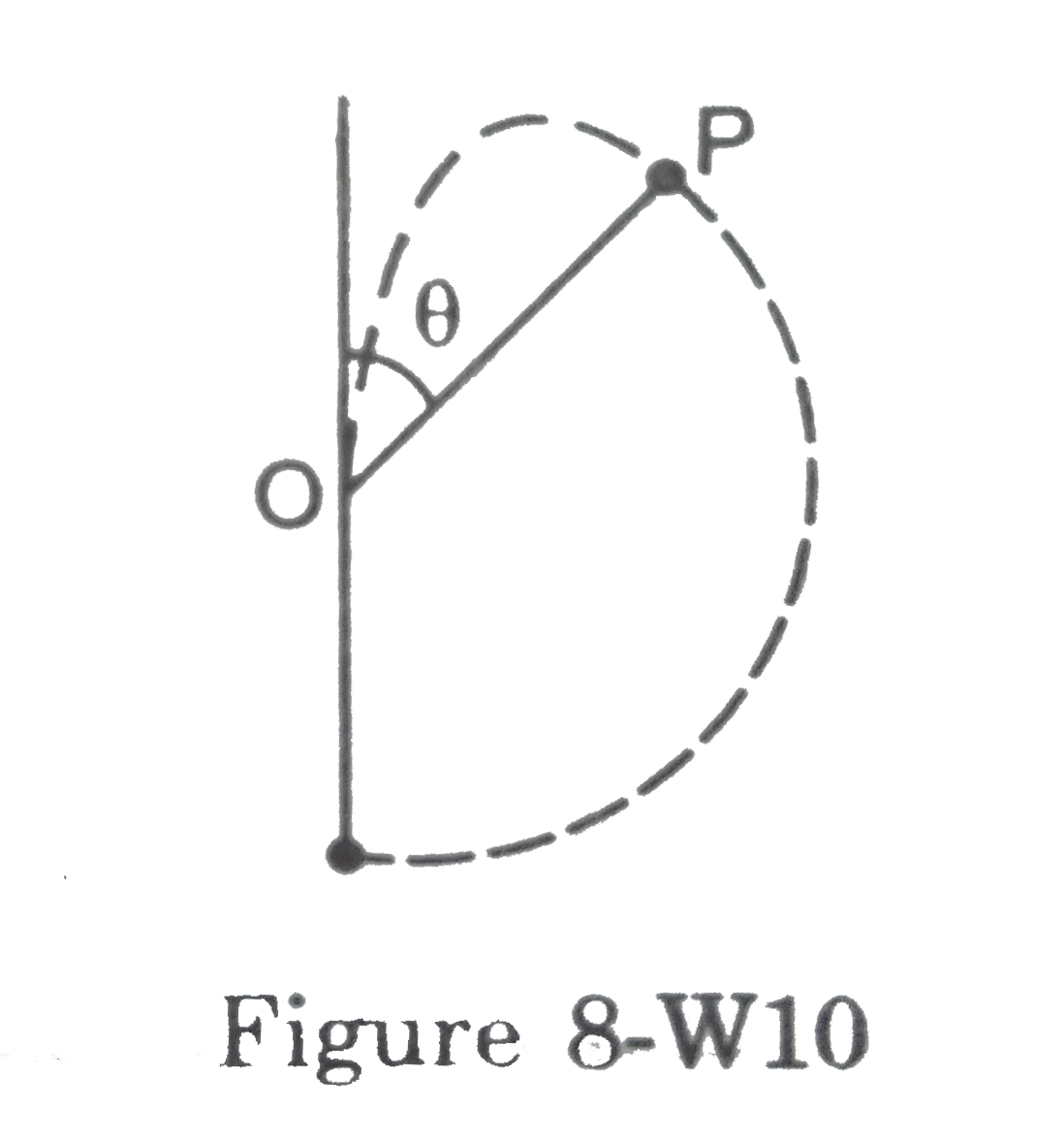
Suppose the string becomes slack when the particle reaches the point P ure. Suppose the string OP makes an angle θ with the upward vertical. The only force actig on the particle at P is its weight mg.The radia component of the force is mgcosθ. As the particle moves on the circle upto P,
mgcosθ=m(v2l)
or, v2=glcosθ ...........i
where v is its speed at P. Using conservation of energy,
12mv20=12mv2+mgl(1+cosθ)
or v2=v2_0−2gl(1+cosθ)......ii
From i and ii v20−2gl(1+cosθ)=glcosθ
or, v20=gl(2+3cosθ) .........iii
Now onwards the particle goes in a parabola under the action of gravity. As it passes through the point of suspension O, the equations for horizontal and verticla motions give,
lsinθ=(vcosθ)t
and −lcosθ=(vcosθ)t−12>2
or, −lcosθ=(vsinθ(lsinθvcosθ)−12g(lsinθvcosθ)2
or −cos2θ=sin2θ−12g(lsin2θ)v2cosθ
or −cos2thet=1−cos2theata−12glsin2θ2glcos2θ[omi]
or, =12tan2θ
ortanθ=√2
From iii v0=[gl(2+√3)]12
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Short Answer15videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Objective 110videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Exercises64videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises57videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
A heavy particle is usspended by a 1.5 m long string . It is given a horizontal velocityof √57ms. a. Find the angle made by the string with the upward vertical, when it becomes slack. B. Find the speed of the particle at this instant. c.Find the maximum height reached by the particle over the point of suspension. Take g=10ms2
View Solution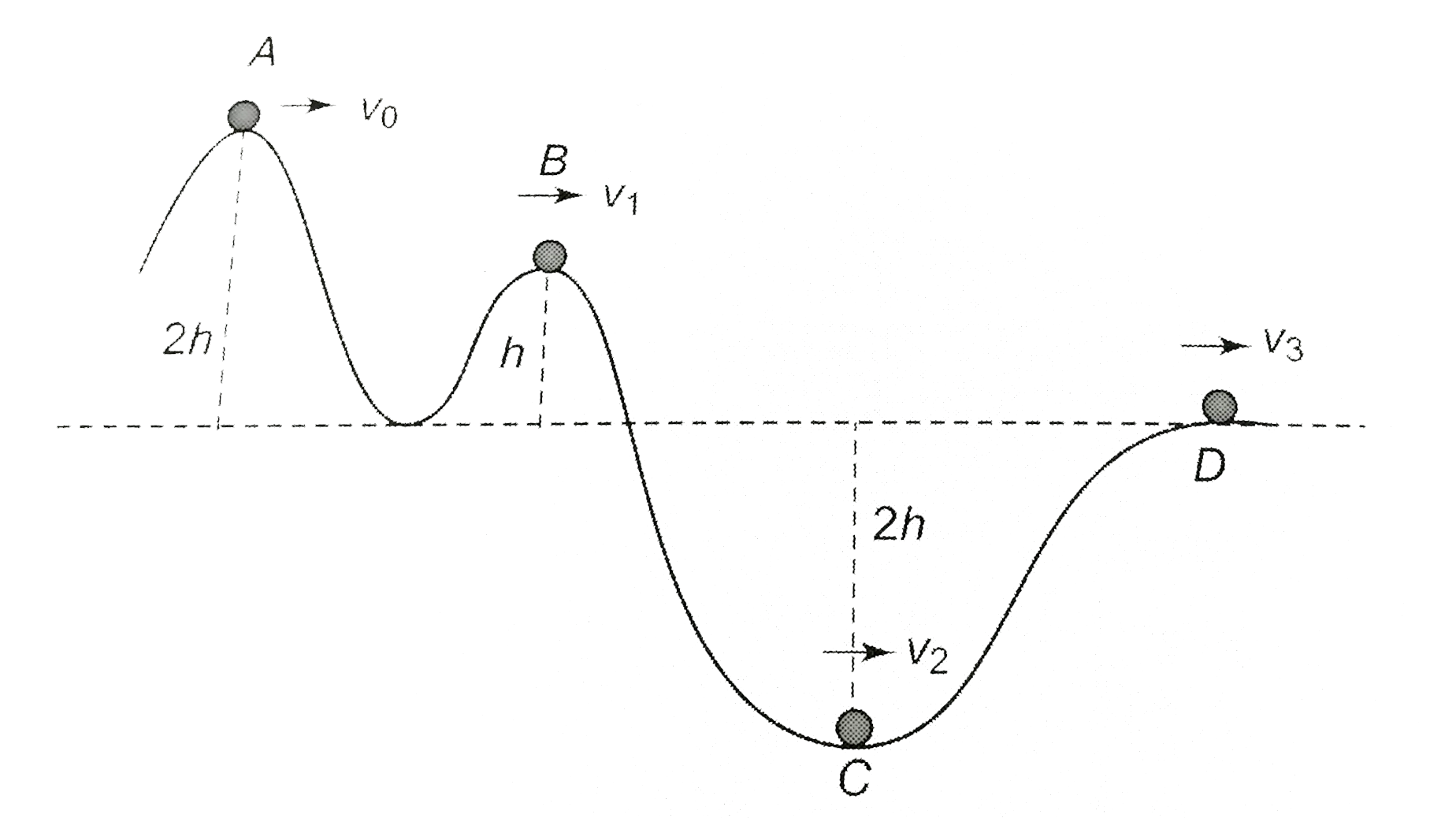
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12 - Question 2 - Select One
A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
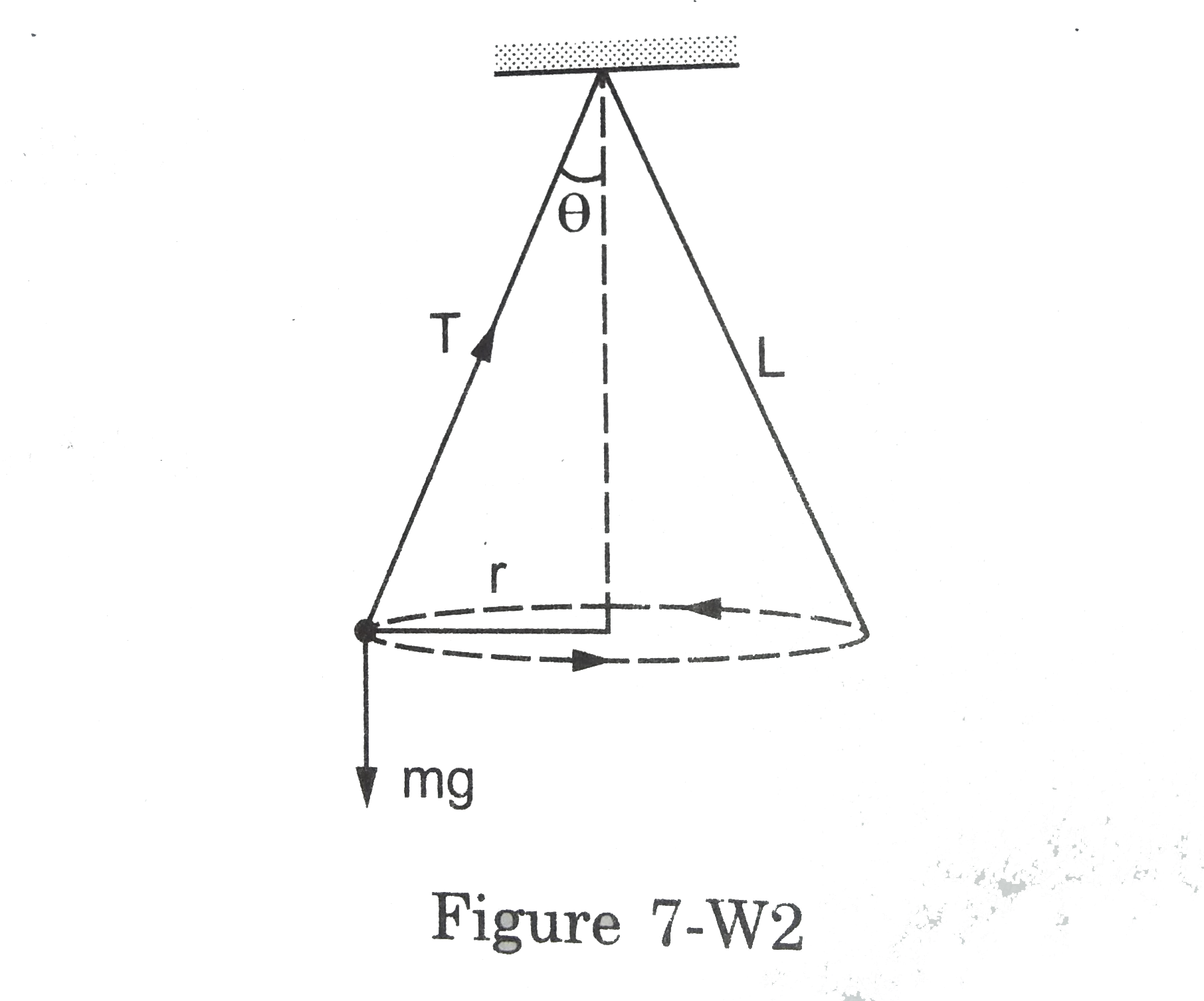
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14 - Question 3 - Select One
A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
 A2qEm(√lg)BqEm(√lg)CqEm(√2lg)DqE2m(√lg)
A2qEm(√lg)BqEm(√lg)CqEm(√2lg)DqE2m(√lg)
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View SolutionFind min velocity v0 such that particle cross the ring.
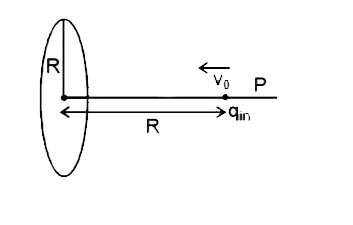 View Solution
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe acceleration of particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be.
View Solution

