A hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length l is as shown in figure. What is the net resistance between the inner and outer surfaces?
3πR2pl
pR2π
pIn(2)2πl
pln(2)l
The correct Answer is:C
To find the net resistance between the inner and outer surfaces of a hollow cylinder with specific resistance ρ, inner radius R, outer radius 2R, and length l, we can follow these steps:
Step 1: Understand the Geometry
We have a hollow cylinder with:
- Inner radius = R
- Outer radius = 2R
- Length = l
Step 2: Consider a Differential Ring
To calculate the resistance, we consider a thin cylindrical shell (ring) at a radius r with thickness dr. The area of cross-section A of this ring is given by:
A=2πr⋅l
Step 3: Calculate the Differential Resistance
The resistance dR of this thin ring can be calculated using the formula for resistance:
dR=ρ⋅dlA
Here, dl is the length of the ring, which is dr. Substituting A and dl into the equation, we get:
dR=ρ⋅dr2πr⋅l
Step 4: Integrate to Find Total Resistance
To find the total resistance R between the inner and outer surfaces, we need to integrate dR from R to 2R:
R=∫2RRdR=∫2RRρ⋅dr2πr⋅l
Step 5: Solve the Integral
The integral ∫drr is lnr. Therefore:
R=ρ2πl(lnr)2RR
Evaluating the limits:
R=ρ2πl(ln(2R)−ln(R))
Using the property of logarithms ln(a)−ln(b)=ln(ab):
R=ρ2πlln(2RR)=ρ2πlln(2)
Final Result
Thus, the net resistance R between the inner and outer surfaces of the hollow cylinder is:
R=ρln(2)2πl
We have a hollow cylinder with:
- Inner radius = R
- Outer radius = 2R
- Length = l
To calculate the resistance, we consider a thin cylindrical shell (ring) at a radius r with thickness dr. The area of cross-section A of this ring is given by:
A=2πr⋅l
The resistance dR of this thin ring can be calculated using the formula for resistance:
dR=ρ⋅dlA
Here, dl is the length of the ring, which is dr. Substituting A and dl into the equation, we get:
dR=ρ⋅dr2πr⋅l
To find the total resistance R between the inner and outer surfaces, we need to integrate dR from R to 2R:
R=∫2RRdR=∫2RRρ⋅dr2πr⋅l
The integral ∫drr is lnr. Therefore:
R=ρ2πl(lnr)2RR
Evaluating the limits:
R=ρ2πl(ln(2R)−ln(R))
Using the property of logarithms ln(a)−ln(b)=ln(ab):
R=ρ2πlln(2RR)=ρ2πlln(2)
Thus, the net resistance R between the inner and outer surfaces of the hollow cylinder is:
R=ρln(2)2πl
Topper's Solved these Questions
Similar Questions
Knowledge Check
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is p. The resistance of . the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρl
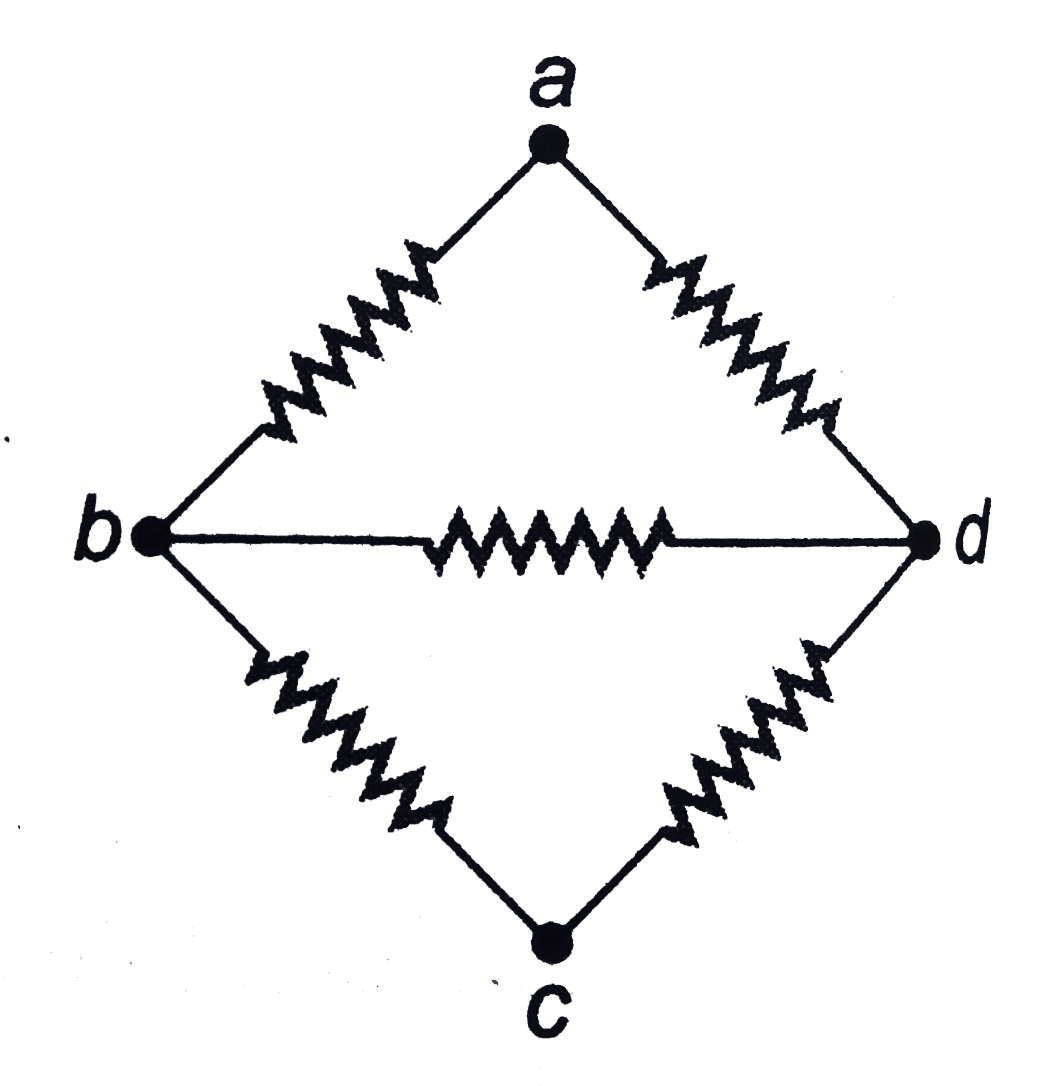
Each resistance of the network shown in figure is r. Net resistance between
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA hollow cylinder with inner radius R. Outer radius 2R mass M is rolling with speed of it's axis v. What is its kinetic energy ?
 .
.
View SolutionConsider a hollow cylinder of length L and inner radius a and outer radius b, as shown in figure. The material has resistivity ρ.
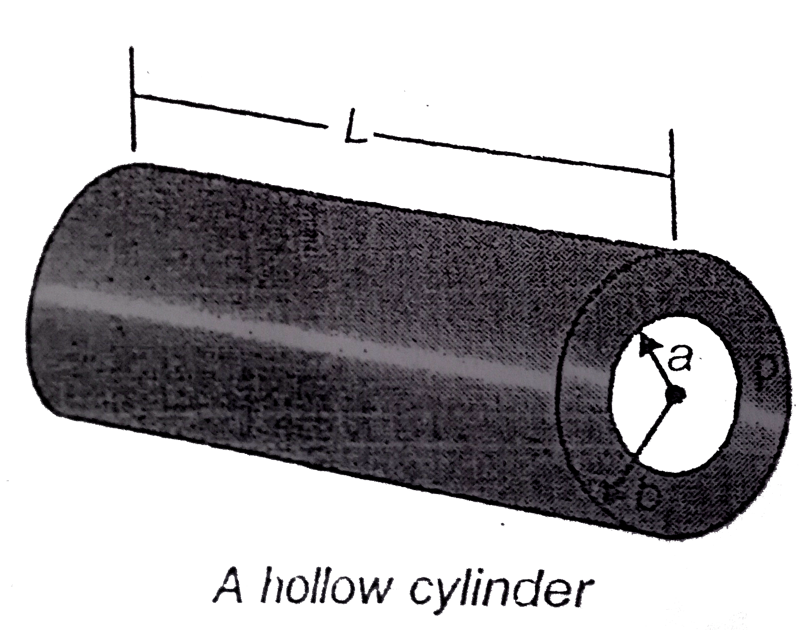
(a) Suppose a potential difference is applied between te ends of the cylinder and produces a current parallel to the axis. What is the resistance measure ?
(b) If instead the potential difference is applied between the inner outer surfaces so that current flows radially outward, what is the resistance measure ?
View SolutionA cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View SolutionA cylinderical tube of length L has inner radius a and outer radius b. What is the resistance of the tube between its inner and outer surface ? Given that the resistivity of its material is ρ.
View Solution
